Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Undamped MDOF System
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll explore how mode shapes are mathematically formulated in undamped linear multi-degree-of-freedom systems. Can anyone tell me what makes a system multi-degree-of-freedom?
Isn’t it that such a system can move in multiple directions?
Exactly! MDOF systems can vibrate in various modes. We model this using the equation: [M]{u¨} + [K]{u} = 0. What do the matrices [M] and [K] represent?
[M] is the mass matrix, and [K] is the stiffness matrix.
Correct! The mass matrix describes how mass is distributed, while the stiffness matrix relates to how the structure resists deformation. Understanding these matrices is crucial for deriving mode shapes.
Harmonic Solutions and the Eigenvalue Problem
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To find mode shapes, we assume a harmonic solution in the form of {u(t)} = {ϕ}sin(ωt}. What do you think {ϕ} represents?
{ϕ} represents the mode shape, right?
That's right! After substituting this into our governing equation, we arrive at the eigenvalue problem: ([K] - ω²[M]){ϕ} = 0. Why is this formulation important?
It helps us determine the natural frequencies and their corresponding mode shapes!
Exactly! Understanding these dynamic properties is crucial for designing structures that can withstand seismic activity.
Implications of Eigenvalues and Eigenvectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s talk about the significance of our results. What do eigenvalues and eigenvectors tell us?
Eigenvalues are the natural frequencies, and eigenvectors are the corresponding mode shapes.
Correct! Knowing the natural frequencies helps us understand how structures will respond during vibrations. Why is knowing the mode shape important when considering seismic analysis?
Because it shows us how the structure will deform, and we need to know that to avoid resonance!
Great point! Designing against resonance is critical in earthquake engineering to prevent structural failure.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the mathematical foundation for mode shapes in MDOF systems governed by a set of matrices representing mass and stiffness, leading to an eigenvalue problem. This formulation reveals the natural frequencies and corresponding mode shapes essential for dynamic analysis in structural engineering.
Detailed
In the context of seismic design and structural dynamics, mode shapes represent the specific deformation configurations that structures assume during free vibration at their natural frequencies. The mathematical formulation is derived from the governing equation for an undamped linear MDOF system:
\[ [M]{u¨} + [K]{u} = {0} \]
Where [M] is the mass matrix and [K] is the stiffness matrix, and {u} is the displacement vector. By assuming a harmonic solution of the form \({u(t)} = {ϕ}sin(ωt)\), the governing equations simplify to the eigenvalue problem:
\[ ([K] - ω^2[M]){ϕ} = {0} \]
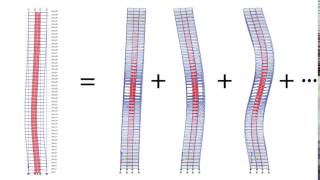
Here, ω represents the natural frequency, and {ϕ} denotes the mode shape or eigenvector. The solution to this eigenvalue problem provides eigenvalues (the squares of the natural frequencies) and eigenvectors (the mode shapes), which are essential for understanding the dynamic behavior of structures under seismic loads.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of MDOF System Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider an undamped linear MDOF system governed by:
[M]{u¨}+[K]{u}={0}
Where:
• [M] = Mass matrix
• [K] = Stiffness matrix
• {u} = Displacement vector
Detailed Explanation
This chunk introduces the basic equation governing a multi-degree-of-freedom (MDOF) system. The equation [M]{u¨}+[K]{u}={0} represents how the mass ([M]) and stiffness ([K]) of a structure relate to its motion ({u}). This is fundamental in the study of vibrations in structures, particularly how they respond to forces without any damping, meaning they continue to vibrate without losing energy.
Examples & Analogies
Imagine a room full of pendulum clocks. Each clock's swinging (like the displacement vector {u}) is affected by its own mass (weight) and the way it's attached (stiffness). The room (the system) can be thought of as one big MDOF system where each clock's movement contributes to the overall behavior of the room's atmosphere.
Assumption of Harmonic Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assuming a harmonic solution of the form:
{u(t)}={ϕ}sin(ωt)
Substituting and simplifying leads to the eigenvalue problem:
([K]−ω²[M]){ϕ}={0}
• ω = natural frequency
• {ϕ} = mode shape (eigenvector)
Detailed Explanation
In this chunk, we assume that the displacement of the system can be described using harmonic motion, which is a sinusoidal function represented by {u(t)}={ϕ}sin(ωt). When we substitute this assumption into the governing equation, we arrive at an eigenvalue problem involving the stiffness matrix ([K]), the mass matrix ([M]), and the natural frequency (ω). The eigenvalues denote the square of the natural frequencies at which the system can oscillate, and the eigenvectors represent the mode shapes.
Examples & Analogies
Think of a swing at a park; when you pull it back and let go, it swings back and forth in a predictable, repetitive motion (harmonic). The swing's motion can be described by its position at various points in time, similar to how the model captures the shape of the swing's path during its oscillation.
Eigenvalue Problem and Its Outputs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This formulation yields eigenvalues (natural frequencies squared) and eigenvectors (mode shapes).
Detailed Explanation
After setting up the eigenvalue problem, solving it provides two important outputs: eigenvalues and eigenvectors. Eigenvalues are essentially the squares of the natural frequencies of the system, reflecting the types of oscillation the system can have. Eigenvectors, or mode shapes, describe how different parts of the structure will move relative to one another at those frequencies. Understanding the relationship between natural frequencies and their corresponding mode shapes is essential for predicting structural behavior under dynamic loads.
Examples & Analogies
Consider a music note played by a guitar string; the pitch (frequency) can change depending on how tightly the string is pulled (akin to the stiffness of a structure). Each unique way the string vibrates when plucked corresponds to different eigenvectors (the mode shapes), where each shape might produce a different sound (or response in a structure).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mode Shapes: Patterns of deformation at natural frequencies during free vibration.
-
Mass Matrix [M]: Represents the mass distribution in the dynamic system.
-
Stiffness Matrix [K]: Describes the resistance of the structural system to deformation.
-
Eigenvalue Problem: Mathematical expression allowing for the derivation of natural frequencies and mode shapes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a 3-degree-of-freedom shear building, three unique mode shapes exist, each displaying varying floor displacement profiles.
-
For a cantilever beam, the mode shapes appear similar to sine waveforms with increasing numbers of curvatures indicating higher modes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In dynamic design, with masses aligned, the mode shapes will be well-defined.
📖 Fascinating Stories
-
Imagine a building swaying in the breeze; with each wave, it finds ease—a dancer knowing its rhythm, it spins at the right frequency.
🧠 Other Memory Gems
-
M for Mass, K for Kinetics; mode shapes define how they behave in specifics.
🎯 Super Acronyms
MODE
- Movement Of Dynamic Energy
- identifying how structures behave.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MultiDegreeofFreedom (MDOF)
Definition:
A system that can experience motion in multiple independent directions.
-
Term: Mode Shape
Definition:
The specific deformation pattern of a structure at a particular natural frequency during free vibration.
-
Term: Mass Matrix [M]
Definition:
A matrix that represents the mass distribution in a dynamic system.
-
Term: Stiffness Matrix [K]
Definition:
A matrix that describes the stiffness characteristics of a structural system.
-
Term: Eigenvalue Problem
Definition:
A mathematical formulation that leads to the determination of natural frequencies and mode shapes of a system.
-
Term: Natural Frequency (ω)
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.