Free Vibration and Mode Shapes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Free Vibration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re talking about free vibration. Can anyone tell me what free vibration is?

Isn't free vibration when a structure vibrates without any external forces acting on it?

Exactly! Free vibration occurs after an initial disturbance, like pushing a swing and letting it go. It’s crucial to understand how structures behave without additional forces.

So, it’s like a pendulum swinging back and forth once it’s been pushed?

Right! And in multi-degree-of-freedom systems, multiple independent modes of vibration combine during free vibration. Can anyone tell me what determines these modes?

Is it the natural frequency and mode shapes?

Correct! Each mode shape corresponds to a specific natural frequency. We'll explore what these mode shapes look like and how they are derived.

In summary, free vibration is key to understanding how structures respond dynamically.
Understanding Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss mode shapes. Who can explain what a mode shape is?

It’s the pattern of deformation structure takes at a specific natural frequency, right?

That's correct! Each mode shape represents a unique deformation pattern. In a building, for instance, a 3-DOF shear building will have three distinct mode shapes. Can you picture what they might look like?

I imagine they would look different based on how each floor moves.

Well done! Understanding these shapes is vital for earthquake-resistant design. Can anyone explain why it’s crucial?

If we know how buildings will deform during an earthquake, we can design them to handle the stress better.

Exactly! Mode shapes give insights into dynamic responses and are essential for ensuring structures don’t resonate destructively. Remember, the number of possible mode shapes equals the number of degrees of freedom.

In summary, mode shapes are significant in predicting structural response during seismic events.
Applying Mode Shapes in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

So now we've established what mode shapes are. How do we apply this knowledge in engineering practice?

Maybe by using them to optimize designs for buildings?

Absolutely! By identifying mode shapes, we can modify geometry or stiffness to improve performance and resistance against vibrations, especially during earthquakes.

How do we ensure buildings don't resonate?

Good question! We analyze mode shapes to identify possibly dangerous resonances, optimizing designs to avoid them. This process includes understanding modal participation factors.

So if we find a mode shape that has too much participation in a certain frequency, we can change the design?

Exactly! Design optimization is a continuous process, and mode shapes play a critical role. Let's summarize: mode shapes help mitigate seismic risks effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Free vibration describes the motion of a system influenced only by its natural frequencies and mode shapes, representing deformation patterns at these frequencies. This understanding is crucial for designing earthquake-resistant structures, as these patterns reveal how structures will behave dynamically under seismic forces.
Detailed
Free Vibration and Mode Shapes
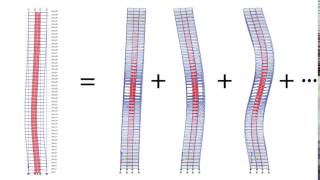
In this section, we explore the pivotal concepts of free vibration and mode shapes within the realm of structural dynamics. Free vibration occurs when a system oscillates without external forces, initiated by an initial disturbance. In multi-degree-of-freedom (MDOF) systems, the response is typically a combination of several independent modes of vibration, each characterized by a unique natural frequency and corresponding mode shape. A mode shape is essentially the deformation pattern exhibited by a structure at a specific natural frequency during free vibration.
- Each mode shape correlates to one natural frequency, and the total number of potential mode shapes corresponds to the number of degrees of freedom (DOFs) in the system.
- For example, a 3-DOF shear building will have three distinct mode shapes representing different vertical displacement profiles across its floors.
Understanding mode shapes is critical, particularly in the context of earthquake engineering, as it allows engineers to design structures that can withstand seismic events effectively, minimizing the likelihood of catastrophic failure due to resonance or amplified motions. In subsequent sections, we will explore the mathematical formulation of mode shapes, their properties, methods of computation, and their interpretations in structural dynamics.
Youtube Videos




![Lecture 3 Free Vibration Analysis, Examples [ Structural Mechanics ]](https://img.youtube.com/vi/WxLLH1lkHgo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Free Vibration
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Free vibration refers to the vibration of a system without any external force, after an initial disturbance.
Detailed Explanation
Free vibration occurs when a system is set in motion from an initial position without any ongoing external influences. Once released, the system vibrates at its natural frequencies, which are inherent to its physical properties. Understanding free vibration helps engineers predict how structures will behave when subjected to forces such as earthquakes.
Examples & Analogies
Imagine pushing a swing; once you stop pushing, the swing keeps moving back and forth on its own. This is similar to free vibration—it continues to oscillate until it's eventually stopped by friction or air resistance, just as a building vibrates until it stops.
Combination of Independent Modes
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In multi-degree-of-freedom (MDOF) systems, the vibration response is a combination of several independent modes of vibration, each with a unique natural frequency and mode shape.
Detailed Explanation
In systems with multiple ways to move (like many buildings), each way of moving is identified as a 'mode.' These modes are independent, meaning each one can vibrate separately, but together they influence the overall response of the structure. Each mode is characterized by its own natural frequency—that is, the frequency at which it naturally wants to vibrate.
Examples & Analogies
Think of a guitar; when you pluck a string, it vibrates at specific frequencies based on its tension and length. A guitar with six strings produces multiple notes independently, just like a structure vibrates in different modes, each affecting the sound it produces.
Understanding Mode Shapes
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A mode shape is the deformation pattern of a structure at a specific natural frequency during free vibration.
Detailed Explanation
A mode shape describes how different parts of a structure move during vibration. It defines the relative motion of each part of the system at a specific frequency, helping engineers visualize how the entire structure will behave when it vibrates. This is crucial for predicting how structures interact with seismic forces.
Examples & Analogies
Consider a trampoline. When you jump on it, it doesn't just bounce up and down; different parts may sag or bulge in unique ways—this is like a mode shape, where each movement pattern corresponds to a specific frequency of vibration.
Degrees of Freedom and Mode Shapes
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Each mode shape corresponds to one natural frequency. The number of possible mode shapes is equal to the number of degrees of freedom (DOFs) in the system.
Detailed Explanation
In engineering, the term 'degrees of freedom' refers to the different ways a structure can move or deform. For each DOF, there exists a corresponding mode shape that describes the deformations at the natural frequency associated with that DOF. If a structure has three DOFs, there will be three different mode shapes.
Examples & Analogies
Think of a puppet on strings—each string represents a degree of freedom. When you pull one string, it moves in a specific way, dramatically changing its position. In a similar way, each mode shape shows a distinct pattern of movement influenced by the structural parameters.
Example: 3-DOF Shear Building
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For a 3-DOF shear building, three distinct mode shapes will exist, each representing a different vertical displacement profile across the floors.
Detailed Explanation
In a 3-DOF shear building model, each of the three floors can move independently, leading to three different ways the building can vibrate. Each mode shape shows how much each floor moves compared to each other, helping engineers understand how the building would respond during an earthquake.
Examples & Analogies
Imagine a three-story house during a strong wind. Each floor may sway differently; the top floor may sway more, the middle less, and the bottom floor may barely move at all. Observing this independent movement gives us insights into the building's stability.
Key Concepts
-
Free Vibration: Oscillation without external forces.
-
Mode Shape: Deformation pattern of the structure at a natural frequency.
-
Degrees of Freedom: Number of independent motion parameters.
-
Natural Frequency: Frequency at which a system oscillates naturally.
Examples & Applications
In a 3-DOF shear building, each floor experiences distinct vertical displacements during free vibration, depicting three unique mode shapes.
For a cantilever beam, the mode shapes can be visualized as sine waveforms, with the first mode showing a single curvature and subsequent modes showing more complex curvatures.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
On a swing and without a pull, free vibration’s motion can be quite full.
Stories
Imagine a tall building swaying gently back and forth. Each sway tells a story of how every floor dances in its own way—this dance follows a pattern known as a mode shape, embodying the natural frequency of the building's response during an earthquake.
Memory Tools
F-M-N: Free vibration indicates the Modes shape at Natural frequencies!
Acronyms
FVM = Free Vibration and Mode Shapes - the essential concepts for dynamic stability.
Flash Cards
Glossary
- Free Vibration
The oscillation of a system without external forces after an initial disturbance.
- Mode Shape
The characteristic deformation pattern of a structure at a specific natural frequency during free vibration.
- Degrees of Freedom (DOFs)
The number of independent parameters that define the state of a mechanical system.
- Natural Frequency
The frequency at which a system tends to oscillate in the absence of damping.
Reference links
Supplementary resources to enhance your learning experience.
