Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Forced Vibration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will be learning about forced vibrations in Single Degree of Freedom systems. Can anyone tell me what we mean by 'forced vibration'?
Isn’t it when an outside force continuously excites the system?
Exactly! The equation we use for forced vibration in SDOF systems is mx¨ + cx˙ + kx = F_0 sin(ωt). Here, what do each of the symbols represent?
m is mass, c is damping, k is stiffness, and F_0 is the external force amplitude.
And ω is the frequency of the external force, right?
Correct! Now, let’s talk about the responses of the system. Can anyone tell me the difference between transient and steady-state responses?
The transient response decays with time, but the steady-state response persists.
Great summary! Remember, the steady-state response dictates the long-term behavior of our structures.
Resonance Phenomenon
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand forced vibrations, let’s explore resonance. What happens when the frequency of the external force matches the natural frequency of the system?
That’s when resonance occurs, and it can lead to large oscillation amplitudes.
Exactly! Resonance is crucial in earthquake engineering since it can cause structures to vibrate uncontrollably. How can we mitigate this risk?
We can shift the natural frequency or add damping to the system!
Yes, by introducing sufficient damping, we can reduce the impact of resonance significantly.
Calculating Steady-State Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s discuss how to quantify the steady-state amplitude. The formula is $$ X = \frac{F_0}{\sqrt{(k - mω^2)^2 + (cω)^2}} $$. Can someone break this down for me?
F_0 represents the applied force, and the denominator calculates the effective stiffness and damping!
Exactly! The relationship indicates that as the external frequency approaches the natural frequency, our amplitude peaks. Why do you think this is important in design?
Because if we design a structure with a natural frequency close to expected external forces, we might get dangerous resonant oscillations!
Great observation! Always remember to assess natural frequencies during structural design to enhance safety.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the mathematical modeling of forced vibrations in SDOF systems, characterized by an external harmonic force. The response of these systems includes both transient and steady-state components, with key concentration on resonance phenomena and amplitude of vibration.
Detailed
Forced Vibration of SDOF Systems
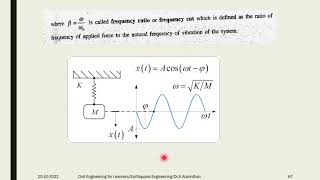
In Single Degree of Freedom (SDOF) systems, forced vibrations arise when external forces continuously impact the system. The equation governing this behavior is represented as:
$$ mx¨ + cx˙ + kx = F_0 sin(ωt) $$
Where:
- m is the mass
- c is the damping coefficient
- k is the stiffness
- F_0 is the external force magnitude
- ω is the frequency of the external force
The solution to this equation can be divided into two main components:
- Transient Response: This part of the solution decays over time and is significant only for a brief period after the external force is applied.
- Steady-State Response: This component reflects the system's long-term behavior and is influenced heavily by the frequency of the external force relative to the system's natural frequency.
Steady-State Amplitude is quantified using:
$$ X = \frac{F_0}{\sqrt{(k - mω^2)^2 + (cω)^2}} $$
The amplitude reaches its maximum when the frequency of the external force is close to the natural frequency of the system, a condition that leads to resonance. This phenomenon can cause dramatic increases in vibration, necessitating careful analysis during design phases to mitigate the risk of structural failure due to excessive oscillation.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Forced Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a harmonic external force F(t)=F_0 sin(ωt), the equation becomes:
mx¨ + cx˙ + kx = F_0 sin(ωt)
Detailed Explanation
This chunk introduces the concept of forced vibration in Single Degree of Freedom (SDOF) systems. Forced vibration happens when an external force continuously acts on the system. The external force is represented as a sine function, indicating that it varies periodically over time. The equation combines the mass (m), damping (c), and stiffness (k) effects to understand how these components react to the imposed force.
Examples & Analogies
Imagine pushing a child on a swing at regular intervals. The force you apply (pushing) alters how high the swing goes. If the pushes are timed perfectly to match the swing's natural rhythm, your pushes will enhance the swing's motion, leading to larger swings—this is akin to forced vibration.
Response Components: Transient and Steady-State
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution has two parts:
- Transient response: Decays with time
- Steady-state response: Dominates at long times
Detailed Explanation
The response of the system can be broken down into two main components. The transient response occurs immediately after the force is applied and consists of initial oscillations that gradually disappear over time. The steady-state response, however, is what we observe after a long time has passed, where the system oscillates at a consistent frequency and amplitude. This concept helps engineers predict how structures will behave under continuous external forces.
Examples & Analogies
Think of a car radio. When you first turn it on, you might hear some static (transient response) as the system settles on a station. After a moment, the music comes through clearly (steady-state response). Similarly, structures will respond initially to forces but will stabilize to a predictable behavior over time.
Determining Steady-State Amplitude
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Steady-state amplitude is given by:
X = F_0 / (k - (mω²))
This amplitude peaks near the natural frequency, causing resonance when ω ≈ ω_n.
Detailed Explanation
The steady-state amplitude X shows how much the system will vibrate under the influence of the external harmonic force F_0, while taking into account the spring constant (k) and the inertia of the mass (m). It highlights that the amplitude of oscillation will peak when the frequency (ω) of the applied force is close to the system's natural frequency (ω_n). This phenomenon is known as resonance, which can significantly amplify the system's response.
Examples & Analogies
Consider a swing again, but this time, think about timing your pushes. If you push the swing at just the right moments (matching its natural swing frequency), it will go much higher than if you pushed at the wrong times. This is the same idea as resonance—small inputs can lead to much larger outputs if timed correctly!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Forced Vibration: Continuous external excitation leading to sustained oscillation.
-
Transient Response: Decays over time after the force is applied.
-
Steady-State Response: Long-term behavior dominated by constant forces.
-
Resonance: Occurs when excitation frequency matches natural frequency.
-
Amplitude: The maximum displacement of the system from its equilibrium position.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A child swings on a swing set, experiencing forced vibration through their movement.
-
A suspension bridge swaying in the wind, where the wind serves as an external force inducing vibrations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When forced vibes start to dance, Beware of resonance, take a chance!
📖 Fascinating Stories
-
Once a bridge swayed gently in the breeze during a storm. But with each gust, it felt the force of the wind pulling it closer to danger—resonance, looming overhead until safety measures were placed.
🧠 Other Memory Gems
-
FRS | Forced vibration, Resonance, Steady-state response — keep these at hand when engineering structures!
🎯 Super Acronyms
TRS | **T**ransient, **R**esonance, **S**teady-state — remember the three responses of forced vibrations!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Forced Vibration
Definition:
A type of vibration that occurs when an external force regularly excites a system.
-
Term: Transient Response
Definition:
The part of the system's response that diminishes over time after the external force is applied.
-
Term: SteadyState Response
Definition:
The long-term behavior of a system under continuous external force.
-
Term: Resonance
Definition:
A phenomenon that occurs when the frequency of the external force matches the system's natural frequency, causing large amplitude oscillations.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate when not subjected to a continuous external force.