Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Base Excitation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will learn about how structures respond to ground motion, especially during earthquakes. Can anyone tell me what happens to a building when the ground shakes?
The building can move or shake, right?
Exactly! This shaking is due to dynamic forces at the base of the structure, known as base excitation. We can model it mathematically. Does anyone remember the basic equation of motion for such a situation?
Is it something like mx¨ + c(x˙ - y˙) + k(x - y) = 0?
Well done! In this equation, $x$ is the displacement of the structure and $y$ is the ground displacement. By analyzing this, we can understand the relative displacement and calculate how buildings will react under seismic loads.
So, how does that help us in real-world design?
Great question! It lays the groundwork for response spectrum analysis, which helps engineers design buildings that can withstand earthquakes.
Can anyone summarize what we've learned so far?
We've learned about base excitation and how to represent it with equations, and why it's essential for earthquake engineering.
Relative Displacement and Its Importance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the concept of base excitation, let's dive deeper into relative displacement. Can anyone tell me the relationship between ground displacement and structural displacement?
Relative displacement is the difference between the two, right?
Correct! We denote this as $u = x - y$. This relative displacement is crucial because it tells us how much the structure is moving relative to the ground.
Why is this difference significant during an earthquake?
Excellent question! It determines the forces acting on the building and how they affect its stability. If we ignore this relative motion, we could severely underestimate the forces involved.
So, tracking that displacement helps us ensure safety?
Precisely! In response spectrum analysis, understanding relative displacement ensures that we design structures capable of enduring earthquakes without collapsing.
Can anyone summarize today's key takeaways?
We discussed the relationship between ground and structural displacement, emphasizing how it's vital for safety during earthquakes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how earthquakes induce dynamic forces at the base of structures, leading to relative displacements. It introduces the mathematical model for describing structural response to ground motion and lays the groundwork for response spectrum analysis.
Detailed
Response of Structures to Ground Motion
During seismic events, structures experience dynamic forces primarily at their base, a phenomenon modeled using the equation:
$$ mx¨ + c(x˙ - y˙) + k(x - y) = 0 $$
Here, $y(t)$ represents the displacement of the ground, and the relative displacement $u = x - y$ simplifies our equation to:
$$ mu¨ + cu˙ + ku = -my¨ $$
This basic formulation helps in analyzing how structures react when subjected to ground motion, and it forms the foundation for response spectrum analysis, a crucial technique in earthquake engineering. Understanding these dynamics is vital for ensuring that buildings can withstand seismic events without experiencing significant structural damage.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
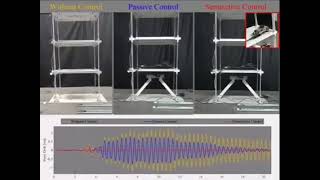
Dynamic Forces from Earthquakes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Earthquakes apply dynamic forces at the base of a structure, modeled by base excitation:
mx¨+c(x˙−y˙)+k(x−y)=0
Where y(t) is the ground displacement.
Detailed Explanation
When an earthquake occurs, it exerts dynamic forces directly at the foundation or base of structures. This interaction is crucial because it significantly impacts how buildings respond to the shaking. The mathematical expression shown here represents a model of these forces, where 'm' represents mass, 'c' is the damping coefficient, 'k' is the stiffness, 'x' is the movement of the structure, and 'y' is the displacement of the ground. The equation illustrates the relationship between the forces due to ground motion and the structure's response.
Examples & Analogies
Imagine a tall tree (the structure) swaying during a windstorm (the earthquake). The strong gusts of wind push the tree from its base, causing it to sway or bend, similar to how dynamic forces from an earthquake affect buildings.
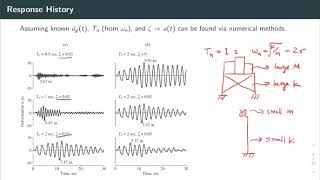
Understanding Relative Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Relative displacement u=x−y, leads to:
mu¨+cu˙+ku=−my¨.
This model forms the basis for response spectrum analysis.
Detailed Explanation
In this model, 'u' represents the relative displacement between the structure and the ground, calculated as the difference between their positions (x for the structure, and y for the ground). The derived equation helps us understand how the structure reacts not just to the ground movement but also to its own inertia. This mathematical formulation is fundamental for creating response spectrum analyses that help engineers predict how a structure will behave during an earthquake based on various ground motions.
Examples & Analogies
Think about a person jumping on a trampoline (the structure) while it's being pushed by another person on the ground (the earthquake). The difference in how high each bounces would represent the relative displacement, showing how their movements affect each other.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dynamic Forces: Essential in understanding how ground motion affects structures during earthquakes.
-
Base Excitation: The fundamental model for how seismic activity impacts the base of structures.
-
Relative Displacement: A critical concept in determining the response of a structure to ground motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a recent earthquake, buildings in a fault zone exhibited significant sway due to base excitation, highlighting the need for effective seismic designs.
-
Engineers used response spectrum analysis to design a high-rise building that could withstand the expected ground motion during a seismic event.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the ground starts to shake, listen to the quake; Relative motion tells the tale, don’t let the building fail.
📖 Fascinating Stories
-
Imagine a brave building standing in an earthquake. It feels the ground shake beneath it and sways, but with the knowledge of relative displacement, it remains intact, adjusting to the forces as they push and pull.
🧠 Other Memory Gems
-
Remember B for Base and R for Relative; Base excitation is where it starts, and Relative displacement is the heart.
🎯 Super Acronyms
B.R.E.A.D - Base Excitation, Response, Engineering Analysis, Displacement.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dynamic Forces
Definition:
Forces that vary with time, particularly significant in ground motion during earthquakes.
-
Term: Base Excitation
Definition:
The forces applied at the base of a structure due to ground motion.
-
Term: Relative Displacement
Definition:
The difference in displacement between the structure and the ground.
-
Term: Response Spectrum Analysis
Definition:
A method used to evaluate the dynamic response of structures subjected to seismic activity.