Vibration Response Parameters
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Amplitude
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start by defining amplitude. Amplitude is the maximum displacement from the mean position. Why do you think amplitude is important in vibration response?

It shows how far a structure can move, right? If it's too much, it could be dangerous.

Yes, and it can affect how structures are designed to withstand earthquakes.

Exactly! The amplitude gives us a measure of how much displacement occurs and can help assess risk. Remember, a larger amplitude means greater potential for structural damage.

So, should we limit the amplitude when designing buildings?

Yes, that's correct! Limiting amplitude ensures that a building can safely dissipate energy during an earthquake.

To sum up, the amplitude indicates the overall response of the structure to dynamic loading and is a key factor in design considerations.
Frequency Response and Phase Angle
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's discuss frequency response. Can anyone explain what it represents?

It's the relationship between the amplitude of the response and the frequency of the excitation, right?

Good! The frequency response plot tells us how different frequencies affect the response of the system. And what about phase angle?

Isn’t it the delay between the applied force and the response of the system?

Exactly! The phase angle is crucial for determining resonance. Can anyone remind me of the resonance condition?

When the frequency of the excitation equals the natural frequency of the structure!

Correct! Remember, at resonance, the amplitude can significantly increase due to constructive interference.

To summarize, both frequency response and phase angle are essential for predicting how structures will behave under dynamic loading.
Logarithmic Decrement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's now explore logarithmic decrement. This measures damping in underdamped systems. What do you think it helps us determine?

It helps us quantify how quickly vibrations decrease over time.

That's exactly right! It’s calculated using the logarithm of the ratio of successive amplitudes. Why is damping significant in our discussions about vibrations?

It helps to dissipate energy, so structures won’t shake too much.

And it’s crucial for preventing excessive displacement during an earthquake!

All valid points! Logarithmic decrement provides insights into the energy dissipation mechanism, which is important for designing resilient structures.

In summary, logarithmic decrement allows us to understand the damping characteristics of structures and their ability to handle dynamic loads.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses critical vibration response parameters such as amplitude, phase angle, frequency response, and logarithmic decrement, which are essential for analyzing and designing structures to withstand dynamic loads, particularly in earthquake engineering.
Detailed
Vibration Response Parameters
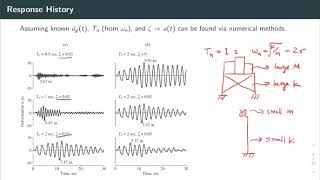
The vibration response parameters are essential for understanding how structures respond to dynamic loads such as those experienced during earthquakes. Key parameters include:
- Amplitude: Defined as the maximum displacement of the vibrating structure from its mean position, indicating how far the system moves from equilibrium.
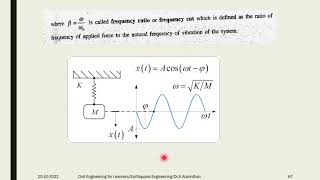
- Phase Angle: It represents the phase difference between the external excitation and the system's response, crucial in determining resonance effects.
- Frequency Response: A graphical representation plotting amplitude against frequency, showing how a system's amplitude varies with different frequencies of excitation.
- Logarithmic Decrement: This parameter quantifies damping in underdamped systems and is calculated using the natural logarithm of the ratio of successive amplitudes over a full cycle of vibration.
Understanding these parameters is vital for designing earthquake-resistant structures that can minimize potential damage and ensure safety during seismic events.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Amplitude
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Amplitude: Maximum displacement from the mean position.
Detailed Explanation
Amplitude refers to the greatest distance a vibrating object moves away from its rest position, or mean position. In simpler terms, if you imagine one end of a spring as you pull it and let it go, the amplitude is how far it stretches or compresses from its natural 'at rest' state. This is a crucial concept in vibration analysis, as it indicates how much motion is experienced by the structure undergoing vibrations.
Examples & Analogies
Consider a swing in a park. When a child swings back and forth, the amplitude would be the maximum height reached at either side of the swing from the center. The higher the swing goes (greater amplitude), the more attention you might need to pay to make sure it's safely anchored.
Phase Angle
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Phase angle: The lag between the excitation and response.
Detailed Explanation
The phase angle indicates how much the output or response of a system (like a building during an earthquake) lags behind the input or excitation (the ground motion). When something vibrates, not all parts of it move perfectly in sync; some may start moving slightly later than others. This lag is what we call the phase angle and it is important for understanding how vibrations can amplify or reduce each other in a system.
Examples & Analogies
Imagine a group of dancers trying to perform a synchronized routine. If one dancer starts their move later than the others, that difference in timing is like the phase angle. If phase angles are not well managed in structures, it can lead to undesirable effects during events like earthquakes.
Frequency Response
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Frequency response: Plot of amplitude vs frequency.
Detailed Explanation
Frequency response is a graphical representation showing how the amplitude of a response changes with different frequencies of excitation. Engineers use this plot to determine how a structure reacts to various frequencies present in seismic events. It helps identify resonant frequencies where the structure might experience large vibrations, which is crucial for ensuring safety during earthquakes.
Examples & Analogies
Think about a musician with a guitar. When they strum the strings (input), certain notes (frequencies) sound louder than others; this is similar to the frequency response of a building. Some frequencies resonate with the guitar's body, causing those notes to ring out beautifully. Conversely, if a building's resonance matches an earthquake's dominant frequency, it might amplify the shaking and lead to problems.
Logarithmic Decrement
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Logarithmic decrement: Measures damping in underdamped systems:
( x(t) )
δ=ln
x(t+T)
Where T is the period of vibration.
Detailed Explanation
Logarithmic decrement is a measure used to quantify how a vibrating system loses energy over time, particularly in systems that are underdamped (where oscillations gradually reduce). It helps to assess the damping characteristics, showcasing how quickly oscillations decrease in amplitude after each cycle. The formula uses the logarithm of the ratio of displacements at two successive peaks to measure energy dissipation.
Examples & Analogies
Imagine ringing a bell. At first, the sound is clear and loud, but as it rings, the sound gets softer until it's barely audible. The logarithmic decrement would measure how quickly the sound fades. Understanding this helps engineers design structures that retain stability during seismic activities and gradually dampen vibrations instead of allowing them to rattle uncontrollably.
Key Concepts
-
Amplitude: Indicates maximum displacement during vibration, crucial for design safety.
-
Phase Angle: Represents the time delay between excitation and response, impacting resonance behavior.
-
Frequency Response: A crucial tool for understanding how different frequencies affect structure response.
-
Logarithmic Decrement: Important for quantifying damping effects in vibratory systems.
Examples & Applications
Example 1: A bridge that sways with an amplitude of 0.5 meters during strong winds. This value helps engineers ensure the structure can handle such deflections.
Example 2: A building's resonance frequency matching the frequency of seismic waves during an earthquake leads to potentially destructive amplifying effects.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the buildings sway, loud and bright, remember amplitude keeps it right!
Stories
Once, a building named Amie learned that her amplitude, when too high, could cause a cries. She stayed low during the storms, ensuring safety was her norm.
Memory Tools
A-P-F-L: Amplitude, Phase angle, Frequency response, Logarithmic decrement - the order to remember key concepts in vibrations.
Acronyms
A-P-F-L for Amplitude, Phase angle, Frequency response, and Logarithmic decrement in vibration response parameters.
Flash Cards
Glossary
- Amplitude
Maximum displacement from the mean position of a vibrating system.
- Phase Angle
The lag between the excitation applied to a system and its response.
- Frequency Response
A plot that shows how the amplitude of a system's response varies with frequency.
- Logarithmic Decrement
A measure of damping in underdamped systems, calculated using the natural logarithm of successive amplitudes.
Reference links
Supplementary resources to enhance your learning experience.
