Application of Linear Momentum
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum in Fluids
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss the application of linear momentum in fluid mechanics. Linear momentum is crucial when analyzing fluid flow based on conservation principles.

How do we actually define linear momentum in this context?

Great question! Linear momentum is defined as the product of mass and velocity, represented by the equation p = mv. It's essential to remember that momentum is a vector quantity.

And how do we apply this, especially in fluid mechanics?

In fluid mechanics, we often deal with momentum conservation through Reynolds transport theorem, where we consider flow through control volumes.

What are control volumes, and why are they important?

Control volumes are defined regions where we analyze fluid behavior. They help us understand how mass and momentum fluxes interact in various systems.

Can you summarize the importance of these concepts?

Certainly! Understanding linear momentum allows engineers to predict fluid behavior efficiently, design systems, and ensure adherence to foundational physical principles.
Momentum Equations and Flow Conditions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's delve into momentum equations. These equations allow us to analyze fluid movement under specified conditions.

What conditions should we consider when applying these equations?

We mainly consider steady flow conditions, meaning there are no changes in pressure or velocity through time.

What about cases with varying pressure?

For non-steady flows, we might need to incorporate time variances into our equations, complicating our calculations.

Can you provide an example of these equations in action?

Absolutely! Let's consider a case where water jet strikes a deflector. By applying momentum continuity, we can calculate the force on the jet.

That sounds interesting! What's the key takeaway from today’s session?

The key takeaway is to recognize when to use momentum equations effectively and how they correlate with flow conditions.
Practical Example: Water Jet and Deflector
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's analyze a practical example: a tank issues a water jet that strikes a deflector at an angle. We know the velocity and discharge; let’s compute the forces involved.

What are the key parameters we need for this calculation?

We need the velocity of the water jet, the area, and the angle of deflection. These will help us find the force exerted on the deflector.

And how do we compute the force?

We apply the momentum equation, considering the mass flow rate and how the velocity changes upon striking the deflector.

Can we assume any simplifications in such problems?

Yes! Often we can assume steady flow and uniform velocity distribution for simplification.

Let’s summarize the process of dealing with these problems.

Absolutely! Identify the parameters, define the control volume, apply the momentum equations, and compute.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the principles of linear momentum as applied in fluid mechanics, highlighting its significance in real-world scenarios, particularly when analyzing flow through control volumes, steady-state conditions, and specific examples from GATE problems. Key tips and techniques in utilizing momentum equations are also detailed.
Detailed
Application of Linear Momentum
In this section, we explore the application of linear momentum in fluid mechanics as part of the broader topic of momentum conservation. Linear momentum, described as a vector quantity, is fundamental in analyzing fluid behavior, particularly under steady flow conditions. The momentum equations can be derived from Reynolds transport theorem and applied to cases with one inlet and one outlet, simplifying calculations.
Key Points Covered:
- Conservation of Momentum: Understanding the fundamental principles governing mass inflow and outflow, and how they relate to momentum flux.
- Equations of Motion: When liquid flows through specific surfaces, we utilize momentum equations in both Cartesian and polar coordinates.
- Control Volumes: Emphasis on defining control volumes and surfaces accurately, ensuring to account for force balance, as in free body diagrams.
- Practical Examples: Solving real-world problems, demonstrating how to compute forces acting on various systems based on velocity and discharge data. These examples will illustrate the application of momentum equations in cases like a water jet striking a deflector and flow through elbow systems.
Application Significance: This approach allows engineers to predict fluid behavior and design efficient systems that optimize performance while adhering to fundamental physical conservation laws.
Youtube Videos



![Basics of Linear Momentum: Part 1 [Fluid Mechanics #27]](https://img.youtube.com/vi/lz7hqpqm4aQ/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Linear Momentum Applications
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
One thing you should remember is that this momentum relationship is a vector equation. This means it has three scalar components: x, y, and z components. We have the velocity vectors in the three components, V_x, V_y, V_z. Similarly, we have the force factors, which have three components. The momentum relationship what we have also has three components.
Detailed Explanation
In the context of fluid mechanics, linear momentum refers to the product of mass and velocity of an object and plays a vital role in analyzing fluid flows. The relationship is considered as a vector equation because momentum can be influenced in different directions. This means that when studying fluid motion, we often break it down into x, y, and z components to simplify calculations and better understand the flow dynamics.
Examples & Analogies
Think of a car driving on a road. The car's momentum can change as it speeds up or turns. When we break down the car's movement into parts – how fast it's moving forward (x), how much it's moving side to side (y), and how high it is (z, such as when going uphill) – it becomes much easier to understand and predict its behavior on the road.
Momentum Flux Terms
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The most of the times, when you compute the momentum flux terms, we should look at what is the relationship, what is the angle between velocity vectors and the normal vector to the control surface. If the scalar product of these two vectors is positive, that means it will have a positive flux coming into the control volume. If it is negative, it indicates it is going out from the control volume.
Detailed Explanation
Momentum flux characterizes the quantity of momentum flowing through a unit area per unit time. It's crucial to analyze the angles between the direction of fluid flow (velocity vectors) and the perpendicular direction to the surfaces (normal vectors) of the system. A positive scalar product indicates that momentum is entering the control volume, while a negative value indicates momentum is leaving. This understanding is essential for accurately applying conservation of momentum principles in fluid dynamics.
Examples & Analogies
Imagine standing in front of a garden hose. If the water shoots straight toward you, the momentum is 'positive' because it's flowing into your space. Conversely, if you turn the hose to spray water away from you, the momentum becomes 'negative' because the flow is exiting your space. Understanding these directions helps us predict how water interacts with objects in its path.
Control Volume Concept and Assumptions
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When applying the control volume concept, we often consider the pressure as atmospheric if it exits to the atmosphere and that the flow is subsonic. This assumption is quite valid under specific conditions, allowing for simplification in calculations.
Detailed Explanation
A control volume is a defined region in space where we apply conservation laws, like conservation of mass and momentum. When analyzing flows, especially those that exit to the atmosphere, it’s often assumed that the pressure at these exit points equals atmospheric pressure. This assumption significantly simplifies the calculations, especially for flows that are subsonic (where the speed of the fluid is less than the speed of sound).
Examples & Analogies
Think of a balloon releasing air. As air escapes, its pressure quickly equalizes with the air outside. Analyzing the balloon as a control volume helps us understand how quickly the balloon will deflate (momentum outflow) and how this affects its shape and behavior as the air exits.
Practical Application - Example Problem
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If we consider a tank where water jets strike a deflector, we can calculate the forces generated using the momentum conservation equations. Given specific velocities and flow rates, we can deduce the resulting forces acting on the deflector and any connected systems.
Detailed Explanation
Calculating forces resulting from fluid jet impacts involves applying momentum conservation equations: the rate of change of momentum inside a control volume equals the momentum coming in minus the momentum going out. By knowing the characteristics of the fluid (like density and flow rate) and the angles of deflection, we can systematically calculate the total force exerted on the surface, which is crucial for designing structures that interact with fluid flows.
Examples & Analogies
Consider a water slide: when kids slide down, they hit the water surface at the bottom. The impact creates waves and splashes due to the momentum of the water jet hitting the surface. If we know the speed at which they enter the water and how much water is displaced, engineers can calculate the forces involved to ensure the slide is safe and can handle all the fun!
Key Concepts
-
Control Volume: Defined space where momentum and fluid properties are analyzed.
-
Momentum Conservation: Principle stating total momentum remains constant without external forces.
-
Reynolds Transport Theorem: Framework relating rates of change of quantities inside and across control surfaces.
Examples & Applications
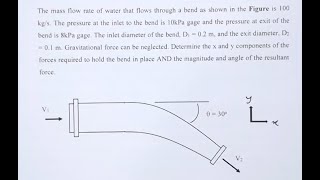
Example of a water jet striking a deflector to calculate forces based on velocity and discharge.
Example analyzing forces in a double exit elbow with given velocities and pressures.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Momentum's like a flowing stream, mass and speed, the perfect team, when they combine, they create a force, guiding our calculations on their course.
Stories
Imagine a water jet hitting a deflector like an arrow finding its target. The angle and speed determine the force, much like a bowstring pulling back, ready to launch.
Memory Tools
Remember M's for velocity in momentum: M = mv!
Acronyms
M.F. for Momentum Flow
= mass
= force.
Flash Cards
Glossary
- Linear Momentum
The product of mass and velocity of an object, represented as p = mv.
- Control Volume
A defined region in space used for analyzing the flow and forces acting on fluids.
- Momentum Conservation
A principle stating that the total momentum in a closed system remains constant unless acted upon by an external force.
- Reynolds Transport Theorem
A theorem that relates the rate of change of a quantity within a control volume to the flux of that quantity across the control surface.
- Steady Flow
A condition where fluid properties at any point do not change over time.
- Momentum Flux
The rate of transfer of momentum per unit area, often used to calculate forces in fluid flow.
Reference links
Supplementary resources to enhance your learning experience.
