Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum Equations
Unlock Audio Lesson
Welcome, class! Today we are going to discuss linear momentum equations. Can anyone tell me what momentum represents in fluid mechanics?
Momentum is the product of mass and velocity.
Exactly! Remember, momentum is a vector quantity, which means it has both magnitude and direction. It's often represented as 'p = mv'.
So, how do we apply this to fluid flow?
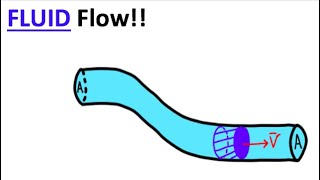
Great question! We can utilize the momentum equations under specific conditions, particularly in steady flow situations. This leads us to the importance of defining control volumes.
What is a control volume?
A control volume is an arbitrary volume in space where we analyze the mass and momentum flows in and out. Think of it like a defined area we are studying.
Got it! So we draw control volume diagrams?
Exactly! This helps visualize the flow and make the application of equations much clearer. Let's recap: momentum is vectorial, and control volumes are key!
Steady Flow Conditions
Unlock Audio Lesson
What do we mean by steady flow conditions?
It means that parameters like pressure and velocity don’t change with time, right?
Precisely! Under steady flow, our equations become much simpler as we can assume uniform conditions over time. This leads us to focus on momentum conservation!
How does momentum conservation apply then?
In a steady flow scenario, the mass inflow equals mass outflow if we consider one inlet and one outlet. This helps us to express conservation of momentum simply by equating the forces.
So, it is important to check if the flow is steady before solving problems?
Absolutely! Always confirm the condition before applying your equations, as it directly affects your results.
Thanks! This is clarifying a lot for me.
I’m glad to hear that! Let's summarize: steady flow means consistent pressure and velocity, making our calculations simpler.
Momentum Flux Terms
Unlock Audio Lesson
Now, let's talk about momentum flux. What is it?
Is it the momentum per unit area?
Exactly! It's calculated based on the flow velocity and the area through which the fluid passes. It’s crucial to relate the velocity vector to the normal vector of the control surface.
How do the angles between vectors affect this?
Great question! The scalar product of the velocity vector and the normal vector indicates the direction of flow. Positive means inflow, and negative means outflow. Understanding this helps in setting up our momentum equilibrium correctly.
So, if I adjust the angle, I can change the influx or outflux signs?
Precisely! The aim is to align these vectors as closely as possible for easier calculations. To reinforce this, can someone give an example of computing momentum flux?
If the velocity is 5 m/s and the area is 1 m², then momentum flux would simply be calculated as 5 kg·m/s, assuming full inflow.
Correct! Summarizing, momentum flux relates to the flow direction and area, impacting our overall calculations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the significance of linear momentum equations within fluid mechanics, providing essential hints and tips for their application, including the importance of steady flow conditions, control volume definitions, and momentum flux terms. It also covers the fundamentals of solving example problems using these concepts.
Detailed
Detailed Summary
In this section, we delve into the critical role of linear momentum equations in fluid mechanics. The discussion begins by revisiting the foundational principle of conservation of momentum, highlighting how it can be applied, particularly in flow scenarios with one inlet and one outlet.
Key Highlights:
- Momentum as a Vector Quantity: It's crucial to remember that momentum equations are vector equations, comprising three scalar components—x, y, and z. When solving problems, it's common to simplify them by focusing on one direction at a time.
- Steady Flow Conditions: The application of momentum equations is valid under steady flow conditions, i.e., when pressure and velocity distributions do not change with time.
- Control Volumes and Diagrams: A key tip is the emphasis on carefully defining control volumes and control surfaces. This visual representation is akin to free body diagrams in solid mechanics and is vital for understanding flow behavior and applying momentum equations correctly.
- Momentum Flux and Correction Factors: Understanding how to compute momentum flux in relation to velocity vectors and their normal components to the control surfaces is crucial. The momentum correction factor (beta) is also discussed, illustrating how it accounts for non-uniform velocity distributions.
- Example Problems: The section includes the solution of practical examples, demonstrating how to apply these principles effectively in real-world scenarios, such as calculating forces on deflectors or analyzing flow through elbows in piping systems.
This section serves as a vital resource for students as they learn to leverage momentum equations effectively in fluid mechanics.
Youtube Videos
![Basics of Linear Momentum: Part 1 [Fluid Mechanics #27]](https://img.youtube.com/vi/lz7hqpqm4aQ/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Vector Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One thing you should remember it this momentum relationship what you get it is a vector equations. That means it has three scalar components, x component, y component and z component. We have the velocity vectors in the three component, Vx, Vy, Vz.
Detailed Explanation
In fluid mechanics, momentum is treated as a vector. This means that it has not just a size (magnitude) but also a direction, which corresponds to the three-dimensional space we live in. Breaking momentum into its x, y, and z components allows us to analyze the forces acting on a fluid in each direction independently. When you apply momentum equations, you generally write separate equations for each direction, which simplifies calculations and helps us understand the flow behavior in a more organized manner.
Examples & Analogies
Imagine driving a car around a corner. Your car's momentum is not only about how fast you're going (which represents magnitude) but also about which direction you're turning. Similar to how you would break down your speed in terms of forward and sideways motion while navigating the turn, we break down fluid momentum into its x, y, and z components to analyze the forces at play more effectively.
Momentum Flux Terms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The most of the times when you compute the momentum flux terms, we should look it what is the relationship, what is the angle between velocity vectors and the normal vector to the control surface.
Detailed Explanation
Momentum flux refers to the amount of momentum passing through a given area per unit time. When analyzing this, it's crucial to consider the angle between the velocity vectors (which represent the fluid's movement) and the normal vectors to the control surfaces (which represent how the surfaces interact with the fluid). If the angle is such that the scalar product of these vectors yields a positive result, it implies that the fluid is entering the control volume; a negative result indicates that it is exiting. Understanding this relationship allows engineers to apply the correct signs and compute forces more accurately.
Examples & Analogies
Think of a water hose spraying water at different angles. If you spray directly into a wall (angle of 0 degrees), the water hits with more impact. But if you spray it at an angle (let’s say 45 degrees), the force and how the water interacts with the wall changes. In fluid dynamics, understanding how these vectors interact helps us determine how effectively we can utilize the momentum from the flowing water.
Momentum Flow Correction Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Most of the times the flow are not uniform velocity distributions. Because of that, we should have the momentum flow correction factor beta because of the velocity distributions is not uniform.
Detailed Explanation
In real systems, fluid flow is often not uniform due to various factors such as friction, changes in cross-sectional area, or obstructions. To account for this variability, we introduce a correction factor known as beta (β). When the velocity distribution is homogeneous across a section, β is equal to 1. However, if the flow is non-uniform, β will be greater than 1 to account for the increased momentum flux due to higher velocities in certain areas. Understanding how to apply this correction factor is critical for accurate calculations of forces and momentum in fluid systems.
Examples & Analogies
Consider a river where most of the water flows in the center while the edges are slower due to vegetation and friction. If you want to calculate how much water is flowing past a particular point, simply averaging the flow rate across the entire width won't give you an accurate result. Instead, you need to account for the faster flow in the middle by using a correction factor. This is similar to how engineers adjust calculations for non-uniform velocity distributions in pipes and channels.
Control Volume Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Within the control volumes we do not talk about how the flow variations are there, the pressure variations and velocity variations or the density variations we do not consider that inside the control volume.
Detailed Explanation
In fluid mechanics, defining a control volume allows us to isolate a specific region of fluid for analysis. Within this control volume, the complexities of variations such as pressure, velocity, or density inside the fluid are simplified. Instead, we consider net inflows and outflows and overall changes to evaluate the system's behavior. This approximation can effectively simplify fluid dynamics equations and allow engineers to design systems without delving into microscopic variations, which can be too complex to compute.
Examples & Analogies
Think of a coffee cup. Instead of analyzing how individual coffee grains behave and move, you might just consider the overall flow of coffee when you stir it. You know that if you stir quickly, coffee will move uniformly instead of studying every grain of coffee. Similarly, in engineering, we often look at the big picture using control volumes to make analysis manageable and practical.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of Momentum: The principle that the total momentum of a closed system remains constant unless acted on by an external force.
-
Steady Flow: Flow condition where fluid properties remain constant over time at specific points in the flow.
-
Control Volume Definition: A defined space where mass and momentum interactions are analyzed.
-
Momentum Calculation: Involves the relationship between velocity, area, and density of the fluid.
-
Momentum Flux: Represents the conveyance of momentum through a given area.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating forces on a deflector when water is redirected by 45 degrees.
-
Analyzing flow dynamics in a double exit elbow in piping.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For momentum that’s linear, just think mass and speed, stay steady, steady flow is what you need!
📖 Fascinating Stories
-
Imagine a water fountain where a stream of water shoots straight up. This steady flow represents how the velocity and pressure stay constant, aligning perfectly with conservation laws!
🧠 Other Memory Gems
-
Control Volume is C-V: Charles Values are Constant Visually.
🎯 Super Acronyms
SFC
- Steady Flow Conditions = Steady Fields Constant.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Momentum
Definition:
A vector quantity defined as the product of mass and velocity.
-
Term: Steady Flow
Definition:
A condition in which fluid properties do not change with time at any given point in the flow.
-
Term: Control Volume
Definition:
A defined volume in space used to analyze mass and momentum transfer.
-
Term: Momentum Flux
Definition:
The rate of momentum transfer through a unit area in a flow field.
-
Term: Momentum Correction Factor (beta)
Definition:
A factor that accounts for velocity non-uniformity across a cross-section in flow.