Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Conservation of Momentum Basics
Unlock Audio Lesson
Good afternoon, class! Today, we are going to explore the conservation of momentum, which is crucial for understanding how fluids behave. Can anyone tell me why this principle is important in fluid dynamics?
I think it's because it helps us predict how fluids will move and interact with objects.
Exactly! The momentum conservation principle helps in forecasting fluid flows in various conditions. Remember, momentum is a vector, meaning it has both magnitude and direction.
So, does that mean we need to consider momentum in the x, y, and z directions?
Absolutely, great observation! We break it down into components. To remember: Use the acronym 'XYZ' for Momentum in the x, y, z directions. Let's move on to its application.
What about when there's a steady flow? Does that change anything?
Good question! In steady flow conditions, the parameters remain constant over time, making calculations easier. We'll dive into examples shortly.
What kinds of examples will we look at?
We will see some practical examples, including a water jet impacting a deflector. Let’s summarize today’s key points... 1) Conservation of momentum is vital for fluid dynamics, 2) Keep in mind vector components, and 3) Steady-state conditions simplify our calculations.
Applications of Momentum Equations
Unlock Audio Lesson
Now, let’s focus on applying the momentum equations in specific scenarios. Can someone explain what a control volume is?
Is it the volume we consider while applying the momentum equations to analyze the flow?
Precisely! The control volume is a defined region where we analyze the fluid flow. When we apply momentum equations, we have to consider pressures and velocities at the boundaries. This is often done with free body diagrams.
Are there any common mistakes when defining control volumes?
Yes! A common mistake is to ignore external forces or friction. Always ensure you evaluate the forces acting on the control volume correctly!
What about when pressure changes?
That's a great point. When flow exits to the atmosphere and is subsonic, we can usually assume atmospheric pressure. It simplifies our equations significantly. Let's recap: Control volumes are crucial in momentum equations, and consider boundary pressures precisely.
Example Problems on Momentum
Unlock Audio Lesson
Let's put our knowledge into practice with some examples. First up, we have a tank with deflectors on a frictionless trolley. Can we determine the force on the spring if the water exits at a velocity of 4 m/s?
We need to use the momentum conservation equations here, right?
Exactly! And don't forget to classify the flow. What type of flow do you think this is?
It’s steady and one-dimensional since the discharge is constant!
Perfect! Now, let’s calculate it. You will use momentum flux and the discharge to find the force. Remember the formula involves density, velocity, and area.
So, the equation becomes F = ρQAcos(θ) where θ is the angle of deflection?
Correct! Always use the right parameters for calculating the forces. Let's summarize; 1) Understand flow types, 2) Apply momentum equations wisely, and 3) Carefully evaluate forces and angles.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this lecture, the conservation of mass and momentum is discussed, focusing on practical application through solving various example problems, including flow structures, steady flow conditions, and control volume analysis. Key tips for applying momentum equations in specific scenarios are also highlighted, ensuring understanding through illustrative examples.
Detailed
Lecture - 14: Conservation of Momentum - Example Problems
In this section, we delve into the concept of conservation of momentum as applied in fluid mechanics. The conservation principles are pivotal in understanding fluid behavior and applying them to solve real-life problems effectively.
Key Topics Covered:
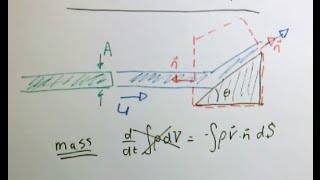
- Review of Previous Concepts: A recap of conservation of mass and momentum, alongside the introduction of momentum equations derived from Reynolds transport theorem, specifically in systems with one inlet and one outlet under steady flow conditions.
- Steady Flow Conditions: An emphasis on how momentum equations apply uniquely under steady flow conditions, where parameters like pressure and velocity remain constant over time.
- Single Direction Application: The ability to simplify complex momentum equations by focusing on specified directions, allowing clearer analysis and solutions.
- Significant Assumptions: Critical points regarding flow with no external forces, the importance of control volumes, and the assumptions related to pressure distributions are discussed.
- Example Problems: Numerous example problems illustrate the application of these principles, including:
- A water jet hitting a deflector mounted on a frictionless trolley.
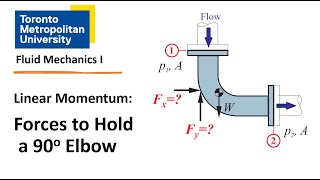
- Forces acting on a double exit elbow.
- A fighter plane refueling example emphasizing momentum changes.
Throughout these examples, the importance of momentum correction factors and appropriate force calculations are highlighted, showcasing how theoretical understanding translates to practical applications.
Youtube Videos
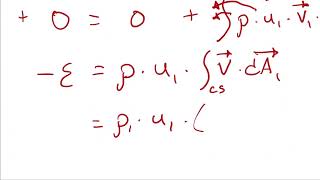
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Momentum Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome all of you for this course on fluid mechanics. In the last class we discussed about conservation of mass and momentum and its applications. To continue to that conservation of mass and momentum and its applications, today I will deliver a lecture on this topic and also I will solve some example problems to illustrate how we can use conservation of mass and momentum equations to solve real life problems.
Detailed Explanation
In this introduction, the lecturer welcomes students to a fluid mechanics course and reviews previous lessons on the conservation of mass and momentum. The aim of today's session is to further explore these concepts through example problems, illustrating their practical applications in real-world scenarios.
Examples & Analogies
Think of momentum conservation like a game of pool. When you strike a ball (momentum), it moves off and strikes another ball, transferring some of its momentum to that ball, causing it to move. In fluid mechanics, we study how fluids also behave similarly when they interact with surfaces and other forces.
Simplifications in Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come back to what we discussed in the previous class that we discussed how we can approximate linear momentum equations from Reynolds transport theorems to specific cases like one inlet, one outlet, which is very simplified problems. And the momentum equation is vector equations. But many of the cases, we can solve problems in specified directions.
Detailed Explanation
The lecturer emphasizes that in fluid mechanics, especially with momentum equations, simplifications are often made. For instance, problems with one inlet and one outlet can be treated as simpler cases. The momentum equations are vector equations that help describe how fluids move in different directions, and although they are complicated, focusing on specific directions can make these calculations manageable.
Examples & Analogies
Imagine solving a puzzle. Sometimes, focusing on the edges first (inlet and outlet) makes it easier to see where the pieces fit. Similarly, simplifying the momentum equations to one inlet and outlet allows us to solve complex fluid dynamics problems more easily.
Steady Flow Conditions in Momentum Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Most important qualities that we consider always is steady flow conditions. This is the approximation we do, the steady flow conditions where there is no change of the pressure or the velocity distributions with respect to time.
Detailed Explanation
Steady flow conditions are crucial in analyzing fluid behavior. In steady flow, the pressure and velocity of the fluid remain constant over time at any given point. This simplifies calculations significantly, allowing engineers and scientists to apply conservation of momentum equations effectively without accounting for time-varying factors.
Examples & Analogies
Think of a river on a calm day. If the water level and speed remain the same throughout the day, you’re observing steady flow. If the river’s flow changes rapidly from rain or dam openings, it becomes complex to predict how the water will behave, similar to fluctuating pressure in a fluid system.
Applying Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can align the specific axis rotation in such a way that using only one equation we can solve the problems. So these are the simplifications for the one inlet, one outlet case, where the mass inflow will be equal to mass outflow.
Detailed Explanation
In this section, the lecturer explains that by setting reference axes properly, they can simplify the momentum equations. In situations with one inlet and one outlet, they can equate mass inflow and outflow to make the calculations more straightforward.
Examples & Analogies
Consider measuring traffic at a one-way street. If you know how many cars come in (inlet) must equal the number that exits (outlet), you can easily assess the flow rate without worrying about complex intersections.
Drawing Control Volumes and Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
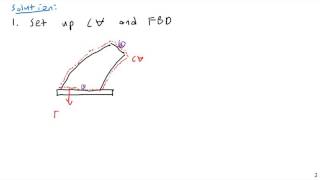
When you apply the linear momentum equations, you have to draw control volume, the control surfaces. How to define this control volume and control surface whether it is a fixed control or movable control is essential.
Detailed Explanation
Defining control volumes and surfaces is a critical part of applying momentum equations. A control volume is a specified region in space where we analyze the flow of fluids and the forces acting on them. Understanding whether these control volumes are fixed or movable helps make sense of how to apply the conservation laws correctly.
Examples & Analogies
Think of a swimming pool as your control volume. If you want to understand how water flows in and out, you need to draw the edges of the pool and observe where water enters and exits. This will guide your understanding and calculations about water conservation in that area.
Momentum Correction Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Also, we talk about the momentum corrections factors that means beta. How do you compute the beta value which is the momentum correction factors.
Detailed Explanation
Momentum correction factors, referred to as 'beta', account for non-uniform velocity distributions in a fluid. When calculating momentum, it is crucial to understand how much the assumed average velocity deviates from the actual velocity across the flow area. Beta helps adjust calculations accordingly.
Examples & Analogies
Imagine a marathon runner who averages 6 minutes per mile but sometimes speeds up or slows down. If you were to calculate their total time, you'd have to consider those variations instead of just the average. Similarly, the momentum correction factor beta adjusts our calculations to accurately reflect variations in fluid velocity.
Example Problem 1: Water Jet
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to today's lectures what I will talk about... we will solve one example, cases where no external forces are there specifically the spacecraft problems that we will solve.
Detailed Explanation
The lecturer sets the stage for practical application by introducing example problems. These problems will help illustrate how to apply the theoretical concepts of momentum conservation in a scenario lacking external forces, akin to conditions experienced by spacecraft.
Examples & Analogies
Think of a spacecraft traveling in the vacuum of space. Without external forces like air resistance, understanding momentum conservation becomes crucial to maintaining its trajectory. Performing these problems helps us understand the fundamental physics that governs these scenarios.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum Conservation: Essential for understanding fluid dynamics and system interactions.
-
Steady Flow: Conditions where parameters remain constant make analysis simpler.
-
Control Volume Analysis: A method important for applying momentum equations effectively.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water jet striking a deflector to analyze forces acting within a moving control volume.
-
Manipulating momentum equations in elbow flows to find force components.
-
Calculating force requirements for an aircraft being refueled mid-flight.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fixed control, fluid flows with grace, steady states keep time in their place.
📖 Fascinating Stories
-
Imagine a hero named Momentum, always in balance, helping fluids navigate through paths without ever losing phase.
🧠 Other Memory Gems
-
Remember 'MCE' for our key concepts: Momentum Conservation, Control Volume, and Equilibrium in equations!
🎯 Super Acronyms
Use 'FACES' to recall Force, Area, Change in Momentum, Energy, and Steady-state in equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Momentum
Definition:
A fundamental principle stating that the total momentum of an isolated system remains constant if no external forces act on it.
-
Term: Control Volume
Definition:
A defined volume in space through which fluid flows and over which mass and momentum equations are applied.
-
Term: Momentum Flux
Definition:
The rate at which momentum passes through a unit area per unit time.
-
Term: Steady Flow
Definition:
A flow condition where fluid properties at a point remain constant over time.
-
Term: Pressure Distribution
Definition:
The variation of pressure within a fluid at different points in space.
-
Term: Frictionless Trolley
Definition:
A theoretical system where no friction acts on the moving body, allowing simplified calculations.