Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Double Exit Elbow
Unlock Audio Lesson
Welcome, everyone! Today we will explore the concept of a double exit elbow. Can anyone tell me what flow classification is?
Isn't it about categorizing the flow based on its characteristics, like steady or unsteady?
Exactly! Flow classification is crucial. In our case, we classify the flow as two-dimensional, steady, turbulent, and incompressible. Remember, the key acronym here is 'STIC'—Steady, Turbulent, Incompressible, and Two-dimensional.
Got it! So, how does this classification help us in solving problems?
Great question! It allows us to apply the right conservation equations. For example, we use mass conservation and momentum equations specific to our classifications. Now, let's dive deeper into momentum conservation!
Momentum Conservation Equations
Unlock Audio Lesson
Now, can anyone explain what momentum flux is?
Is momentum flux the mass flow rate times velocity?
Yes, that's one way to think about it! When we apply the momentum conservation equation in a flowing fluid, we need to consider the momentum flux in and out of the elbow. Remember, it's essential to analyze the directional components as well.
How do we figure out if it's going in or out?
Excellent inquiry! Look at the angle of the velocity vector concerning the control surface's normal vector—this helps determine the flow direction.
So, we keep track of signs based on their direction?
Right again! Always be cautious of the signs in momentum equations—they're key to getting correct forces.
Example Problem Analysis
Unlock Audio Lesson
Let's look at a practical example: a double exit elbow with two distinct exit velocities. We will calculate the horizontal and vertical forces acting on it.
What initial information do we need to proceed?
Good point! We start by identifying the pressures and velocities at each exit, as well as the area of the elbow. Now, can anyone tell me how to set up the mass conservation equation?
We need to express the inflow and outflow in terms of mass flow rates, right?
Absolutely! And remember to check the assumptions we've made regarding steady flow when evaluating our variables. Next, let's derive the force components.
How do we calculate these forces?
We'll apply the momentum equations and remember to break down the velocity into its components aligned with our coordinate system.
Interpretation of Results
Unlock Audio Lesson
After we calculate the force components, what do we take away from the results?
We check if the forces make sense in relation to our flow conditions?
Exactly! Not only do we validate our results, but we also consider how they impact design and application in real-world systems like piping.
I see, so understanding the forces helps in designing better systems?
Precisely! As engineers, we need to ensure that our designs can handle these forces safely and efficiently.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the flow dynamics in a double exit elbow and illustrates the use of momentum conservation principles to derive the forces acting on the elbow from fluid dynamics. This includes detailed examples to interpret these concepts in practical applications.
Detailed
Detailed Summary
In this section on 'Double Exit Elbow,' the fluid mechanics principles of momentum conservation are explained through the analysis of a two-dimensional steady flow in an elbow configuration. The section begins with an overview of how to classify flow in engineering problems, noting characteristics such as whether the flow is turbulent, incompressible, and if it adheres to one-dimensional or steady assumptions. This classification sets the stage for applying conservation equations effectively.
Key formulas derived from Reynolds Transport Theorem (RTT) are utilized to determine both horizontal and vertical force components resulting from fluid flow through the elbow. An example problem details how to calculate resulting forces when specific velocities and pressure conditions exist. Students are guided through the systematic approach to solving these types of fluid mechanics problems, emphasizing the importance of control volumes, average velocity assumptions, and pressure variations.
Visual aids and control volumes' sketches are essential in simplifying complex relationships, leading to clear and usable results. By the end of this section, readers should understand how momentum equations apply in engineering scenarios to derive forces for systems like elbows in piping systems.
Youtube Videos
![Turbulent Flow: Minor Loss Coefficiant Chart [Fluid Mechanics #42]](https://img.youtube.com/vi/_W5ncP-ADmw/mqdefault.jpg)
![Volumetric Flow Rate Example 2: The Gasoline Tank [Physics of Fluid Mechanics #42]](https://img.youtube.com/vi/ZCiBdlUjMqU/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
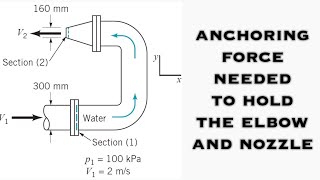
Now let us go to the second example 2 where we have the water flows through a double exit elbow. Okay this is elbow type of concept, where we have a V 1 velocity and V 2 velocity. One is 5 meter per second another is 10 meter per second. Inside the volume of the elbow is 1 meter cube, okay the volume of this. What are the vertical and horizontal force component of from air and water on this elbow if pressure in the free jet is atmospheric and the unit weight of the water will be 1000 kg per meter cube.
Detailed Explanation
In this example, we are dealing with a scenario where water flows through a specially designed elbow, which is a type of bend in a pipe. Here, two different flow velocities are mentioned: V1 at 5 meters per second and V2 at 10 meters per second. The inside volume of the elbow is given as 1 cubic meter. The task is to determine the vertical and horizontal forces acting on the elbow due to water and air. Understanding the pressure conditions is crucial as the pressure in the free jet is atmospheric pressure, and we know the density of water (1000 kg/m³).
Examples & Analogies
Imagine water flowing through a flexible hose that turns at an angle. Depending on how fast the water flows in different sections of the hose, it will exert forces on the walls of the hose. Similarly, in this example, the elbow shape of the pipe influences the flow, affecting how forces are distributed on it.
Flow Classification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Flow classification: Two dimensional, Steady flow, Turbulent, Incompressible.
Detailed Explanation
For this problem, it is important to classify the type of flow based on its characteristics. The flow is considered two-dimensional because we are analyzing it in a plane. It is steady flow since the flow conditions do not change over time. The flow is classified as turbulent indicating that it has chaotic property changes, and it is incompressible since the density of the water remains constant throughout the flow.
Examples & Analogies
Think of driving a car on a straight road versus a winding, hilly road. On the straight road, the conditions (speed, direction) remain steady—similar to steady flow. If the road suddenly spirals down, it mirrors turbulent flow where the conditions change with twists and turns.
Pressure Considerations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if we have this fixed control volumes, first we will find out that the pressures. The pressures at the inlet is given is 25,000 Pascal. At the outlet is pressure is atmospheric pressure. That what is there. So you have the free jet at these two locations where pressure is the atmospheric pressures. At these two point you have a pressure equal to atmospheric pressure, but at this point I have the pressure which is 25,000 Pascal, Newton per millimeter square.
Detailed Explanation
In analyzing the elbow, we first need to determine the pressure values at different points within the control volume. The inlet pressure is specified as 25,000 Pascals (which is a measure of force per unit area), while at the outlets, the pressure is atmospheric, meaning it is the pressure exerted by the weight of air above us. This distinction is vital as it determines how forces act on the elbow structure.
Examples & Analogies
Consider how the pressure in a balloon changes. When you blow air into the balloon, the pressure inside increases (similar to the inlet pressure of 25,000 Pa). However, once you let go, the air exits and the balloon returns to atmospheric pressure, just like the water exiting the elbow to the outside atmosphere.
Applying Mass Conservation Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then we will apply mass conservation equations that let us apply mass conservation equations to compute it what could be the velocity at the section 3. So we are applying the mass conservation equations for these control volumes that to compute what could be the velocity at this point.
Detailed Explanation
The principle of conservation of mass states that the mass flow rate entering a control volume must equal the mass flow rate exiting the control volume. In our elbow, we apply this principle to find the velocity at a certain point in the elbow. The continuity equation helps us relate the inflow and outflow velocities and areas, allowing us to compute unknown velocities based on known data.
Examples & Analogies
Imagine water flowing through a funnel. As it moves from a wide opening to a narrow tube, it speeds up. This speed-up is because of mass conservation: the amount of water must stay the same, but it has to move fast to fit through the smaller space.
Applying Momentum Conservation Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applying RTT, sum of forces should equal to the rate of change of momentum flux within the control volume is equal to the net outflux of momentum flux passing through these control surface.
Detailed Explanation
In the context of fluid dynamics, momentum conservation is a key concept. We apply the Reynolds Transport Theorem (RTT) to relate the change in momentum within the control volume to the forces acting on the elbow. Essentially, we are equating the net forces acting on the fluid to the change in its momentum, allowing us to compute the forces resulting from the fluid flow.
Examples & Analogies
Think of a swimming pool. When a swimmer pushes off the wall, they propel themselves forward. The force they exert on the wall equals the change in momentum they experience. Similarly, in our elbow, the water's momentum change interacts with the elbow's structure, exerting forces.
Final Calculations and Results
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if I apply this part, then F x will come it to the 9539 Newton. Similar way the force component acting on this y direction that one will be the 7720 Newton.
Detailed Explanation
By applying the conservation equations for momentum, we find the forces acting in both the horizontal (Fx) and vertical (Fy) directions on the elbow. The calculations yield values of 9539 Newtons for the horizontal force and 7720 Newtons for the vertical force, providing insight into the resultant forces exerted on the elbow due to the flowing water.
Examples & Analogies
Consider a pizza chef tossing a pizza dough into the air. The force they apply can be thought of in two directions: upward (to get it off the table) and outward (to spread it). In our case, the elbow experiences similar dual directional forces from the water flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum Conservation: The principle that momentum remains constant in the absence of external forces.
-
Flow Classification: The way to categorize fluid motion within systems to apply the correct equations.
-
Control Volume: A defined area for analyzing fluid motion and applying conservation laws.
-
Momentum Flux: A concept crucial for understanding how momentum changes across surfaces in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a double exit elbow with specific velocities used to calculate resultant forces on a system.
-
Analysis of fluid motion in different configurations, allowing for practical application of momentum conservation principles in engineering.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a flow so steady, keep control, momentum stays in a rhythm, that's the role.
📖 Fascinating Stories
-
Once upon a time in a piping system, a double elbow learned to balance forces, where pressure led to decisions of flow.
🧠 Other Memory Gems
-
Remember the acronym 'STIC' for steady, turbulent, incompressible, and two-dimensional — key to flow classification.
🎯 Super Acronyms
MFE = Mass Flow Entry, our guide to fluid processes at elbow exits.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Momentum Conservation
Definition:
A principle stating that the total momentum of a closed system remains constant if no external forces are acting on it.
-
Term: Flow Classification
Definition:
Categorization of fluid flow based on properties such as steadiness, dimensionality, and whether it is turbulent or laminar.
-
Term: Momentum Flux
Definition:
The rate of momentum transfer per unit area, often calculated as the product of density and velocity.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A fundamental theorem connecting the flow of fluids through a control volume to changes in momentum.
-
Term: Control Volume
Definition:
An imaginary boundary defined for analyzing fluid flow, allowing for the application of conservation laws within its limits.