Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Square-root Time Method
Unlock Audio Lesson
Today, we’re discussing the square-root time curve fitting method. This important technique helps us understand how materials consolidate over time. Can anyone tell me what consolidation means?
Is it related to how soil settles under weight?
Exactly! Consolidation refers to the process where soil particles move closer together, often due to the weight of structures above them. Now, why do you think we want to measure how long this process takes?
So we can predict how long we need to wait before building on it?
Right! Understanding the timeframe ensures safety and allows for proper planning. Now let’s discuss how we actually plot this data.
Steps in the Fitting Method
Unlock Audio Lesson
To apply the square-root time method, the first step is to plot our dial readings against the square root of time. What do you think is next?
We need to draw a tangent on the plot?
That's correct! We draw a tangent line to the initial portion, which gives us insight into the initial consolidation behavior. Can someone think of why we use a tangent?
It shows the slope or rate of change at that point, right?
Perfect! The slope of this tangent helps us understand the rate at which consolidation begins. Now, after drawing the tangent, what do we do next?
Critical Intersection Point
Unlock Audio Lesson
Once we have our tangent, we need to draw another line, PR, where the length OR is 1.15 times OQ. Can anyone explain why that ratio might be important?
Maybe it helps to scale the prediction more accurately?
Exactly! This ensures our predictions take into account the consolidated behavior accurately. Now, what happens when line PR intersects the second portion of the curve?
That's the point we mark as S, which indicates when we can expect the consolidation to reach a certain level, right?
That’s correct! This intersection, point S, is crucial for predicting consolidation under field conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the square-root time method is outlined as a technique for predicting the time rate of consolidation in materials. Key steps include plotting dial readings against the square root of time, drawing tangents and lines on the graph, and marking intersections that inform on consolidation behavior.
Detailed
Square-root – time curve fitting method
The square-root time curve fitting method is a vital technique utilized to assess and predict the rate of consolidation in geotechnical materials. This method helps determine how long it will take for a material to consolidate under specific loading conditions by correlating dial readings with the square root of time.
Key Steps in the Method:
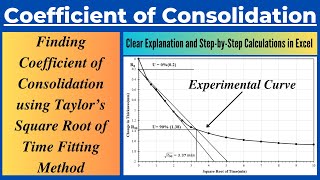
- Plotting Data: Begin by plotting the dial reading against the square root of time (T) for a specific pressure increment.
- Drawing Tangents: A tangent line (PQ) is drawn on the initial portion of the curve, which represents the early behavior of the consolidation process.
- Defining Parameters: A secondary line (PR) is drawn parallel to the tangent line, while the length of this line (OR) is set to be 1.15 times that of OQ, facilitating further analysis.
- Identifying Critical Points: The intersection point (S) of the second portion of the curve with line PR is crucial, as it indicates the predicted consolidation behavior over time.
Significance
The significance of this method lies in its ability to predict the time for a given degree of consolidation based on the drainage path's length, thereby aiding engineers in making informed decisions regarding soil stability and structural design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Plotting the Dial Reading and Square Root of Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Plot the dial reading and square root of time i.e T for a pressure increment as shown in figure.
Detailed Explanation
In this initial step, you begin by constructing a plot that represents two important variables: the dial reading and the square root of time (denoted as T) relative to a specific increase in pressure. The dial reading may represent some measured value in a testing process that changes as pressure is applied, while plotting the square root of time helps visualize how the process evolves over time. This step is crucial as it allows you to see the relationship between these variables in a graphical format, which is essential for further analysis.
Examples & Analogies
Imagine you're tracking how long it takes for a sponge to absorb water. In this scenario, the dial reading represents the amount of water absorbed, while the square root of time indicates how long it has been soaking. By plotting these two values on a graph, you can visually assess the efficiency of absorption over time.
Drawing the Tangent to the Initial Portion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Draw a tangent PQ to the initial portion of the plot as shown in fig.
Detailed Explanation
Once the plot is created, the next step is to draw a tangent line (denoted as line PQ) to the initial portion of the curve. This tangent line represents the instantaneous rate of change at the start of the plot. The slope of this tangent line provides important information about how rapidly the dial reading is changing in response to time during the initial phases of the pressure application, which is crucial for understanding the behavior of the system under study.
Examples & Analogies
Think of a car accelerating from a stop light; initially, the speed increases rapidly. By drawing a tangent at the moment the light turns green, you can see how fast the car is speeding up at that exact moment. This tangent similarly helps us understand the rate of change in our graph during the early stages.
Creating the Line PR
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Draw a line PR such that OR=1.15OQ.
Detailed Explanation
After establishing the tangent line, the next instruction requires you to draw another line (identified as PR) such that its length relation to the previously drawn tangent line PQ indicates that OR is 1.15 times the length of OQ. This step is significant as it adjusts the slope of the line PR in a specific manner, which can be used to predict or analyze future data points on the curve. This adjustment plays a vital role in curve fitting and influences the accuracy in estimating how the system behaves under varying conditions.
Examples & Analogies
Imagine you are scaling a model; you want the new model (PR) to be slightly larger than the original proportion (PQ). If PQ represents the original, adjusting PR to be 1.15 times larger allows you to see how the model behaves under slightly modified conditions, giving you insights into potential changes in performance or behavior.
Identifying the Intersection Point S
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The intersection of the line PR with the second portion of the curve i.e point S is marked.
Detailed Explanation
In the final step of this procedure, you are tasked with finding where the line PR intersects with the second part of the curve (this intersection is labeled as point S). The significance of this point lies in its importance for subsequent analysis or calculations regarding the consolidation process. Marking this point gives a key reference that can help determine how well the model fits the observed data, informing future forecasting or adjustments.
Examples & Analogies
Consider a mountain climbing scenario where you place a marker (point S) at the intersection of two different trails. This marker not only helps guide you in selecting paths in the future but reinforces your understanding of the terrain. Similarly, point S indicates a critical juncture in your measurements that will be vital for future comparisons or assessments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Square-root Time Method: A technique to predict consolidation time in relation to drainage paths.
-
Tangent Line: A line indicating the initial rate of consolidation on a graph.
-
Pressure Increment: The added pressure on soil samples during consolidation tests.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a soil sample is subjected to a pressure increment of 100 kPa, practitioners can use the square-root time method to determine how long it will take for the soil to consolidate under this load.
-
By plotting experimental data, engineers can visualize how different soil types respond to loading over time, facilitating effective design decisions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the pressure mounts and soil is found, consolidation is the name of the round.
📖 Fascinating Stories
-
Imagine a sponge sitting under a book. As the book presses down, the sponge squeezes and settles—a representation of soil consolidation under load.
🧠 Other Memory Gems
-
PLOT (Plot dial reading, Line for tangent, Observe intersection, Time prediction) helps remember the steps of using the square-root method.
🎯 Super Acronyms
SQUARE (Steps, Quality Analysis, Understanding Rate, Establish intersection) reminds us of the key components to remember in this technique.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Consolidation
Definition:
The process by which soil particles are pressed closer together, often due to applied loads, leading to a reduction in volume.
-
Term: Tangent
Definition:
A straight line that touches a curve at a given point without crossing it, used to illustrate the slope at that point.
-
Term: Pressure Increment
Definition:
An increase in pressure applied to a material, typically used in consolidating tests to observe material behavior.
-
Term: Square Root of Time
Definition:
A mathematical transformation of time used to plot variables in consolidation studies.