Derivation of DDF Curves
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to DDF Curves
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

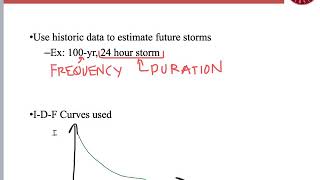
Today, we're going to learn about how we derive Depth-Duration-Frequency curves, or DDF curves. Can anyone tell me what the basic formula to derive DDF curves is?

Is it something like Depth equals Intensity multiplied by Duration?

That's right! DDF curves are derived from the relationship where Depth equals Intensity multiplied by Duration. Why do you think this relationship is important?

Because it helps in calculating rainfall depth for various durations which is useful in hydrology.

Exactly! This helps us in modeling hydrological processes effectively. Remember: DDF is for depth, while IDF is for intensity!
Importance of DDF in Hydrology
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Why do you think DDF curves are particularly useful in hydrology?

They give us the rainfall depth data we need for catchment models.

Exactly! And this depth data is crucial when we are looking at water balance studies. Can anyone summarize how DDF and IDF curves relate?

Well, once we have the IDF curves, we can derive the DDF curves simply by using that depth relationship.

Great! Understanding this relationship will help you in many aspects of hydrological design.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section elaborates on the derivation of DDF curves, explaining that once the Intensity-Duration-Frequency (IDF) curves are established, DDF curves can be readily created using the basic formula that relates depth to intensity over time.
Detailed
Derivation of DDF Curves
The Depth-Duration-Frequency (DDF) curves are essential tools in hydrology that help quantify rainfall depth over specific durations and frequencies. Derived from the previously established Intensity-Duration-Frequency (IDF) curves, DDF curves can be easily constructed using the relationship: Depth = Intensity × Duration. This relationship is particularly significant for hydrological models that require inputs of rainfall depth rather than just intensity. Understanding both IDF and DDF curves is crucial for effective water resources planning and flood management.
Youtube Videos



![Storm Water and Highway Drainage Design & Construction [ DrEYPEI on Water Resources Engineering ]](https://img.youtube.com/vi/b0GSMfyUvGs/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Relationship of DDF Curves
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Once IDF curves are developed, DDF curves can be easily derived since:
Depth=Intensity×Duration
Detailed Explanation
The relationship between Depth, Intensity, and Duration is fundamental in understanding DDF curves. Once we have established the IDF curves, which define the relationship of rainfall intensity over time, deriving the DDF curves becomes straightforward. This is because the amount of rainfall (Depth) can be calculated by multiplying the Rainfall Intensity by its Duration. Therefore, if we know how intense the rainfall is for a certain period, we can easily deduce how much total rain fell during that time period.
Examples & Analogies
Think of a sponge soaking up water. If you know how quickly you are pouring water onto the sponge (Intensity) and how long you pour it (Duration), you can figure out how much water the sponge absorbs (Depth). Just like in rainfall measurements, understanding how these three factors interact helps us manage water resources effectively.
Importance of DDF Relationship
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• The DDF relationship is particularly useful for hydrological models that require rainfall depth inputs.
Detailed Explanation
The DDF relationship is crucial in hydrological modeling, which involves predicting how water will flow through and be managed in a landscape after rainfall. Hydrological models often need inputs that specify how much rainfall will reach the ground over a given time, not just how intense the rainfall is. By using DDF curves, hydrologists can input exact rainfall depth values into their models, leading to better predictions of runoff, flood events, and the saturation of soils.
Examples & Analogies
Imagine you are a gardener planning to water your plants using a hose. Knowing how much water (depth) you need based on how long you'll water (duration) and at what rate (intensity) will help you ensure your plants get the right amount without overwatering. Similarly, in hydrology, using the DDF helps in precisely calculating the water input into models which are critical for planning flood defenses and drainage systems.
Key Concepts
-
DDF curves are derived from IDF curves.
-
The relationship between depth, intensity, and duration is fundamental to hydrological modeling.
Examples & Applications
If the IDF curve indicates a rainfall intensity of 60 mm/hr for a duration of 1 hour, then the corresponding depth using the formula Depth = Intensity × Duration would be 60 mm.
For a duration of 30 minutes with an intensity of 120 mm/hr, the DDF would be 60 mm because 120 mm/hr × 0.5 hours = 60 mm.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Depth's a measure, quick and right, Intensity times duration's height.
Stories
Once upon a time, there was a river that overflowed every time it rained. The wise villagers found out they could predict how deep it would be by measuring how hard it rained and how long it rained, using the magical formula of depth.
Memory Tools
D.I.D - Depth = Intensity × Duration.
Acronyms
DDF
Depth
Duration
Frequency - remember these three to understand rainfall better.
Flash Cards
Glossary
- DDF Curve
A Depth-Duration-Frequency curve that shows the depth of rainfall over various durations for different return periods.
- Intensity
The rate at which rainfall falls, expressed in mm/hr or inches/hr.
- Duration
The length of time over which the rain occurs, measured in minutes or hours.
- Return Period
A statistical measure that indicates the average interval of time between events of a certain intensity or size, also referred to as frequency.
Reference links
Supplementary resources to enhance your learning experience.
