Learn
Games

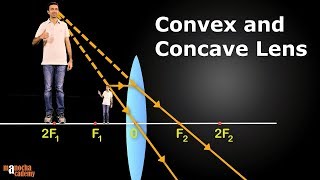
5.4 - Image Formation by Convex Lens

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Position of Object - At Infinity

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, let's explore how a convex lens forms images. First, what happens when the object is placed at a great distance or at infinity?

Student 1
Student 1

Does the image remain the same regardless of the distance?

Teacher
Teacher

Good question! When an object is at infinity, the image is formed at the focus F2, is point-sized, real, and inverted. Remember, it's being focused down to that single point!

Student 2
Student 2

So, it’s kind of like a laser point? Very small?

Teacher
Teacher

Exactly! You could think of a laser pointer creating a small dot of light—that’s like our image at F2. Let's keep that imagery with us as we move on.

Student 3
Student 3

What if we moved the object a bit closer?

Teacher
Teacher

That transitions us to the next position. Let’s delve into what happens when the object is placed beyond 2F1.

Position of Object - Beyond 2F1

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, let’s consider when the object is beyond 2F1. What can we expect from the image?

Student 4
Student 4

Is it still real and inverted?

Teacher
Teacher

Correct! When an object is beyond 2F1, the image is formed between F2 and 2F2. In this case, it is diminished, real, and inverted.

Student 1
Student 1

How about the size? Does it change a lot?

Teacher
Teacher

Yes! The image becomes smaller as the object moves away from the lens. It’s diminished when compared to the object size. This concept can be easily memorized with the phrase: 'Farther means smaller'.

Student 2
Student 2

Can you summarize the key features again?

Teacher
Teacher

Of course! Image is diminished, real, and inverted when the object is beyond 2F1. Great observations, everyone!

Position of Object - At 2F1

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Next, let’s discuss what occurs when the object is positioned right at 2F1.

Student 3
Student 3

Is it when the image is same size as the object?

Teacher
Teacher

Exactly! The image will be formed at 2F2, same size as the object, real, and inverted. Think of this as a perfect reflection.

Student 4
Student 4

So, does it follow the same path or rule as before?

Teacher
Teacher

Yes, it adheres to the rules of ray construction: it’s created following the same distance from the optical center to the focus. An easy way to remember: 'At 2F1, it’s equal in size'.

Student 1
Student 1

Fantastic! What’s next?

Teacher
Teacher

We will explore the case when the object lies between F1 and 2F1 next.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section covers how a convex lens forms images based on the position of the object relative to the lens.

Standard

The section explains the various positions of objects in relation to a convex lens and the characteristics of the images formed. It details how image characteristics such as size and nature (real/virtual, inverted/erect) change depending on the object's position.

Detailed

Image Formation by Convex Lens

The convex lens is a powerful optical tool used to converge light rays. The image formed by a convex lens depends on the object's position relative to the lens. In this section, we explore the various object placements and their corresponding image characteristics:

  1. At Infinity: The image is point-sized, real, and inverted at the principal focus (F2).
  2. Beyond 2F1: The image appears between F2 and 2F2, is diminished, real, and inverted.
  3. At 2F1: The image is at 2F2, has the same size as the object, is real, and inverted.
  4. Between F1 and 2F1: The image is enlarged, real, and inverted, positioned beyond 2F2.
  5. At F1: The image is highly enlarged, real, and inverted, appearing at infinity.
  6. Between O and F1: The image is enlarged, virtual, and erect, appearing on the same side as the object.

Understanding these variations aids in practical applications such as magnifying systems and optical devices.

Youtube Videos

Convex and Concave Lenses
Convex and Concave Lenses
LENSES :CLASS 10 : CBSE & ICSE : CONVEX AND CONCAVE LENS: Characteristic of IMAGE :REFRACTION:
LENSES :CLASS 10 : CBSE & ICSE : CONVEX AND CONCAVE LENS: Characteristic of IMAGE :REFRACTION:
Refraction Through a Lens Class 10 ICSE | Light Physics ICSE Class 10 | @sirtarunrupani
Refraction Through a Lens Class 10 ICSE | Light Physics ICSE Class 10 | @sirtarunrupani
Image formation by convex lens | By Vinod Avnesh
Image formation by convex lens | By Vinod Avnesh
Image formation by CONVEX LENS animation | All 6 cases explained | Professor Phi
Image formation by CONVEX LENS animation | All 6 cases explained | Professor Phi

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Image Formation at Different Object Positions

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Position of Object Position of Image Size Nature
At infinity At F2 Point-sized Real, inverted
Beyond 2F1 Between F2 and 2F2 Diminished Real, inverted
At 2F1 At 2F2 Same size Real, inverted
Between F1 and 2F1 Beyond 2F2 Enlarged Real, inverted
At F1 At infinity Highly enlarged Real, inverted
Between O and F1 On the same side Enlarged Virtual, erect

Detailed Explanation

This chunk presents various scenarios of how a convex lens forms images based on the position of the object in relation to the lens. The key points include:
- At Infinity: When the object is very far away, the image forms at the focal point (F2) and is point-sized, real, and inverted.
- Beyond 2F1: The image forms between F2 and 2F2, is diminished compared to the object, real, and inverted.
- At 2F1: Here, the image is formed exactly at 2F2, maintaining the same size as the object, and is still real and inverted.
- Between F1 and 2F1: The image becomes enlarged, appears beyond 2F2, and remains real and inverted.
- At F1: The image appears at infinity, and is significantly larger than the object—again, it is real and inverted.
- Between O and F1: In this position, the image formed is enlarged and appears upright (erect), and is virtual as it's on the same side as the object.

Examples & Analogies

Think of a convex lens as a magnifying glass. If you hold a magnifying glass very close to a small object like an ant (positioned between O and F1), you can see a large, upright image of the ant through the lens. If you move the magnifying glass away until you hold it far (positioned at infinity), the details of the object become less defined, and the image becomes smaller or point-sized.

Characteristics of Images Formed

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Size and Nature of Images:
- Point-sized, diminishes, or enlarges based on the object's position.
- Images can be real and inverted, or virtual and erect depending on the position of the object.

Detailed Explanation

The characteristics of images formed by a convex lens depend heavily on the object’s position:
- Size: The images can vary from point-sized to highly enlarged. The farther the object is, the smaller the image is up to a point, after which the size toggles back to enlarging with closer object placements.
- Nature: Most images are real and inverted, meaning they appear upside down, except when the object is placed between O and F1, where the image formed is virtual and erect (upright). Real images can be projected onto a screen, while virtual images cannot.

Examples & Analogies

Consider how a projector works. When you shine an image onto a screen (like a movie projector), it projects a real and inverted image. However, putting the same image into a handheld magnifying glass holds it upright and makes it appear larger, similar to how the lens behaves when the object is between O and F1.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Image at Infinity: Point-sized, real, inverted at F2.

  • Image Beyond 2F1: Diminished, real, inverted between F2 and 2F2.

  • Image at 2F1: Same size, real, inverted at 2F2.

  • Image Between F1 and 2F1: Enlarged, real, inverted beyond 2F2.

  • Image at F1: Highly enlarged, real, inverted at infinity.

  • Image Between O and F1: Enlarged, virtual, erect on the same side.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • When an object is placed at 30 cm from a convex lens with a focal length of 12 cm, the image is formed 20 cm away, real and inverted.

  • If an object is 10 cm from a convex lens with a focal length of 15 cm, the image formed is virtual and erect.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • Image at infinity, F2 it does meet, / Real and inverted, it's a tiny feat.

📖 Fascinating Stories

  • Imagine a lighthouse beam shining far at sea. When the lighthouse is bright (object at infinity), the light concentrates at a point (F2) to guide sailors safely home.

🧠 Other Memory Gems

  • Remember: GIFT—G for Great distance (infinity), I for Inverted, F for Focused, T for Tiny.

🎯 Super Acronyms

SMART

  • Same size at 2F1
  • Magnified if within F1 to 2F1
  • A: real
  • varying
  • across all positions
  • Tiny at F2.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Convex Lens

    Definition:

    A lens that is thicker in the middle than at the edges, converging parallel rays to a focal point.

  • Term: Focal Length

    Definition:

    The distance from the optical center to the principal focus.

  • Term: Principal Focus

    Definition:

    The point on the principal axis where light rays converge (for convex lenses) or appear to diverge (for concave lenses).

  • Term: Real Image

    Definition:

    An image that can be projected on a screen, formed on the opposite side of the lens from the object.

  • Term: Virtual Image

    Definition:

    An image that cannot be projected on a screen, formed on the same side of the lens as the object.