Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Distance Formula Introduction
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will learn how to find the distance between two points in three-dimensional space. We can represent any point using coordinates (x, y, z). Can anyone tell me what we would expect to find if we had two points?
I think we need to measure the length between them.
Exactly! We will use a distance formula that's derived from the Pythagorean theorem. Does anyone remember how that theorem works in two dimensions?
Yes, it states that the distance d = β[aΒ² + bΒ²]!
Great! Now, let's extend this to three dimensions. We have an extra term for the z-axis. So, our formula becomes d = β[(xβ - xβ)Β² + (yβ - yβ)Β² + (zβ - zβ)Β²]. Can anyone tell me what each part of this formula represents?
The (xβ - xβ), (yβ - yβ), and (zβ - zβ) parts tell us how far apart the points are along each coordinate axis!
Exactly! Understanding this is essential for nearly all applications in three-dimensional geometry. Letβs summarize: the distance formula incorporates how each spatial dimension contributes to the overall length. Any questions?
Application of the Distance Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we know the distance formula, letβs talk about its applications. Itβs used in various fields, from physics to computer graphics. Can anyone think of how we might use it?
Maybe in navigation systems? They might need to calculate distances between locations!
Absolutely! Now, letβs practice. If P(1, 2, 3) and Q(4, 6, 8) are two points, what is the distance between them?
Um, I think we substitute in the formula: d = β[(4-1)Β² + (6-2)Β² + (8-3)Β²] = β[3Β² + 4Β² + 5Β²] = β[50].
Thatβs correct! The distance is β50 or 5β2. Always remember to break down each step to avoid mistakes. Letβs wrap up by recalling that understanding the distance formula is essential in not just geometry, but many applied sciences.
Visualizing Distance in 3D Space
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, letβs visualize! Imagine plotting points in a three-dimensional space. How would they look on a graph?
They would form a 3D grid! If we connect two points, we can also see the shortest path between them.
Exactly! This is the essence of our distance formula. It connects each point's position to each other. With this understanding, we can explore further spatial geometries.
So, the formula helps us calculate that 'shortest path' you mentioned?
Yes! And the visual representation aids in grasping the concept fully. As you study more about 3D geometry, keep practicing plotting those points because it will greatly enhance your understanding!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The distance between two points represented by coordinates in three-dimensional space is determined using an extension of the Pythagorean theorem. This formula allows us to evaluate spatial relationships and has practical applications in various fields, including physics and engineering.
Detailed
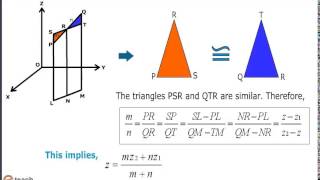
In three-dimensional geometry, the distance between two points P(xβ, yβ, zβ) and Q(xβ, yβ, zβ) can be calculated using the distance formula, which is a direct extension of the Pythagorean theorem from two dimensions. The formula to find the distance d is given by:
d = β[(xβ - xβ)Β² + (yβ - yβ)Β² + (zβ - zβ)Β²]
This formula illustrates how each dimension contributes to the overall distance and emphasizes how geometry in space expands our understanding beyond flat surfaces. Mastering this formula is crucial for tackling more complex topics in three-dimensional geometry.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Distance in 3D
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The distance between points P(x1,y1,z1) and Q(x2,y2,z2) is given by the formula derived from the three-dimensional extension of the Pythagorean theorem.
Detailed Explanation
In three-dimensional geometry, we can calculate the distance between two points in space, say point P with coordinates (x1, y1, z1) and point Q with coordinates (x2, y2, z2). This distance is computed using a formula that stems from the Pythagorean theorem, which is a concept we're already familiar with from exploring two-dimensional space. The formula essentially combines the differences in each coordinate direction (x, y, z) to find the actual distance between these two points in a 3D plane.
Examples & Analogies
Imagine you are in a large room (representing a 3D space) where you need to walk from one corner to another. If you were to measure the distance on the floor (2D), you'd only consider the x and y directions. However, if someone were to lift you up to a shelf (the z direction), the true distance you'd have to travel would need to account for all three movements. Therefore, calculating distance in 3D is like finding out how far you really need to travel when you can move in all three dimensions.
The Distance Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The distance formula in three-dimensional space can be expressed as: D = β((x2 - x1)Β² + (y2 - y1)Β² + (z2 - z1)Β²)
Detailed Explanation
The formula for finding the distance D between points P and Q is: D = β((x2 - x1)Β² + (y2 - y1)Β² + (z2 - z1)Β²). This formula is derived from the Pythagorean theorem. To break it down: First, we find the difference between the x-coordinates (x2 - x1), y-coordinates (y2 - y1), and z-coordinates (z2 - z1). Each of these differences is squared to ensure that we are measuring distance positively. After we sum these squared differences, we take the square root to find the actual distance between P and Q. This gives us a straight line distance connecting the two points in three-dimensional space.
Examples & Analogies
Think of using a GPS to find the shortest path between two buildings located at specific coordinates in a city. Each building's coordinates can be seen as a point in space. The distance formula is like the GPS calculating the direct path between the two buildings, accounting for all three dimensions: the length along the street (x-axis), the width (y-axis), and the height if there are multiple floors (z-axis). Just like the GPS gives you the direct distance no matter the path taken, the distance formula provides that straight-line measurement in our 3D environment.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Distance Formula: Used to determine the distance between two points in space.
-
Extension of Pythagorean Theorem: The formula is based on the Pythagorean theorem adapted to three dimensions.
-
Coordinates: Each point is defined by a set of three coordinates indicating its position.
-
Three-dimensional Geometry: The study of figures and points in three-dimensional space.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Find the distance between the points A(2, 3, 5) and B(5, 7, 10). Solution: d = β[(5-2)Β² + (7-3)Β² + (10-5)Β²] = β[3Β²+4Β²+5Β²] = β[50].
-
Example 2: Calculate the distance between C(-1, -1, 0) and D(2, 2, 3). Solution: d = β[(2 - (-1))Β² + (2 - (-1))Β² + (3 - 0)Β²] = β[9 + 9 + 9] = β[27].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the distance in space, remember the formula, youβll ace!
π Fascinating Stories
-
Imagine A and B in a room. The distance between them can be found with a magical formula β a secret route through space!
π§ Other Memory Gems
-
D = STEP (Subtract, Then Evaluate, Pythagorean).
π― Super Acronyms
D = Distant Points in Dimension.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Distance Formula
Definition:
A mathematical equation used to determine the length between two points in space given their coordinates.
-
Term: Pythagorean Theorem
Definition:
A principle in geometry that expresses the relationship between the lengths of the sides of a right triangle.
-
Term: ThreeDimensional Space
Definition:
A geometric representation that includes three axes: x, y, and z.
-
Term: Coordinate System
Definition:
A system that uses numbers to represent a point in a given space.