7. Introduction to Three-Dimensional Geometry

Welcome class! Today, we will explore an exciting topic: three-dimensional geometry. Can anyone tell me what comes to mind when they think about geometry in three dimensions?

Maybe shapes like cubes or spheres?

Exactly! In three-dimensional geometry, we study various shapes and figures in space using three coordinates: x, y, and z. This lets us analyze distances, directions, and relationships more effectively than in two-dimensional geometry.

So, how do we even begin to represent a point in space?

Great question! A point in three-dimensional space is represented by an ordered triplet (x, y, z), where each letter indicates the position along the respective axis. Let's remember this: 'X marks the spot at the X-axis!'

Now, let’s dive deeper. The axes we just mentioned—x, y, and z—are mutually perpendicular. Who can tell me what that means?

It means they meet at right angles!

Exactly! They intersect at the origin. This setup creates three important coordinate planes: the xy-plane, yz-plane, and zx-plane. Let’s use the mnemonic 'Yummy Zebra Meals' to memorize these planes. Each word starts with the first letter of each plane!

So, if we know the coordinates of a point, how can we identify which plane it's in?

Good question! We determine the position based on whether one or more coordinates equals zero. For example, if z = 0, the point lies in the xy-plane.

Next, let’s discuss how to find the distance between two points in three-dimensional space. Remember the distance formula derived from the Pythagorean theorem? It expands to account for 3D. Can someone remind us what it looks like?

Isn’t it something like the square root of the sum of squared differences?

Exactly! The formula is $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$. To help remember this, think 'Square and be fair, distance divides without care!'

Can we do an example?

Absolutely! For points P(1, 2, 3) and Q(4, 5, 6), let’s find the distance together.

Now, let’s explore the section formula. It helps in finding the coordinates of a point dividing the segment joining two points in space. Does anyone remember how this formula works?

Is it similar to the 2D section formula but with one more coordinate?

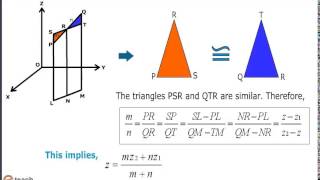
Exactly! For points P(x1, y1, z1) and Q(x2, y2, z2) dividing in the ratio m:n, the coordinates of point R become $R = \left( \frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n}, \frac{mz_2 + nz_1}{m+n} \right)$. A good way to remember is 'Multiply, then Add, and Finally Divide!'

Can we try this out with some numbers?

Definitely! Let’s calculate the division of points A(2, 3, 1) and B(4, 5, 3) in the ratio 1:2.

For our final session today, let’s discuss how points and lines can intersect with coordinate planes. Who can think of a situation where a point might lie on a plane?

If the z-coordinate is zero, it lies on the xy-plane?

Correct! Points where one of the coordinates equals zero will lie on that corresponding plane. Additionally, for lines, if they cross the planes, they may be described as intersecting. Remember: 'Zero is the hero on the coordinate frontier!'

What if a line intersects two planes?

Great observation! Lines can intersect multiple planes, and understanding their equations becomes essential as we progress. Are there any last questions before we finish?

No questions, but I’m excited to apply these concepts!

Fantastic! Keep practicing, and remember to visualize these concepts, as they will be invaluable in your geometry studies.