Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Section Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore the section formula in three dimensions. Who can tell me why we need a section formula in space?
To find points that split a line in a certain ratio!
Exactly! The section formula helps us find coordinates of points that divide segments in given ratios, just like in two dimensions but now extended into three. Can anyone mention what the coordinates of a point are in three dimensions?
It's an ordered triplet: (x, y, z).
Great! So if we have points P and Q with coordinates P(x1, y1, z1) and Q(x2, y2, z2), in the ratio m:n, how do we find point R?
We can use the section formula!
Let's put that knowledge to the test in the next session!
Deriving the Section Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs derive the coordinates of point R using the formula. Can someone remind us of the coordinates of points P and Q?
P has coordinates (x1, y1, z1) and Q has coordinates (x2, y2, z2).
Right! Now, if R divides segment PQ in the ratio m:n, the x-coordinate of R can be expressed as...?
x = (m * x2 + n * x1) / (m + n)!
Perfect! And how about the y-coordinate?
y = (m * y2 + n * y1) / (m + n)!
Great! And similarly for the z-coordinate. Why do we think these formulas are important in practical applications?
They help us find points in geometry and physics!
Exactly. We'll dive into some applications next!
Applications of the Section Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs explore some applications of the section formula! Can anyone give me an example where we might use this formula?
Finding midpoints between two locations on a map!
Absolutely! It also helps in calculations involving centroids of triangles, where we find points dividing the medians. Are there any other areas we could apply this?
In public transport to determine routes?
Yes! This knowledge can aid in optimization problems. For example, helping a delivery service find efficient paths. Letβs summarize this section.
In summary, the section formula is vital for determining coordinates that divide segments in three-dimensional space, enhancing both geometric understanding and practical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section examines the three-dimensional section formula, which calculates the coordinates of a point that divides the line segment joining two points in space. It extends the concept of the section formula from two dimensions into three-dimensional space, allowing for more complex spatial calculations.
Detailed
Section Formula in Three Dimensions
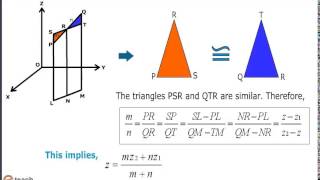
In three-dimensional geometry, the concept of the section formula allows us to determine the coordinates of a point that divides a line segment joining two points in space internally in a given ratio. Given two points in space, P(x1, y1, z1) and Q(x2, y2, z2), and a ratio m:n, the coordinates (x, y, z) of the point R that divides the segment PQ in the ratio m:n can be derived using the following formulas:
Formulas
- x-coordinate:
x = (m * x2 + n * x1) / (m + n) - y-coordinate:
y = (m * y2 + n * y1) / (m + n) - z-coordinate:
z = (m * z2 + n * z1) / (m + n)
Significance
This formula is essential for solving various problems in geometry and spatial analysis, such as finding midpoints, determining centroids of triangular sections, or analyzing sections of three-dimensional figures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Section Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The coordinates of a point dividing the segment joining two points in space internally in a given ratio are given by the three-dimensional section formula, extending the two-dimensional concept.
Detailed Explanation
The section formula is a mathematical tool used to find the coordinates of a point that divides a line segment connecting two points in space. For example, if we have two points A and B defined by their coordinates in three dimensions, the section formula helps us determine the position of a point P that divides the segment AB in a specific ratio, such as 2:3 or 1:4. This method is an extension of the two-dimensional section formula from coordinate geometry.
Examples & Analogies
Imagine you are walking from point A to point B (like from your home to a friend's house). If you want to meet someone at a specific spot before you reach your friend's house, you can use the section formula to figure out exactly where that spot is based on how far you are walking. For example, if you are two-thirds of the way to your friend's house, the formula can pinpoint your exact location along that path.
Understanding Internal Division
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The section formula is specifically focused on points dividing the segment internally.
Detailed Explanation
When we talk about internal division, we mean that the point dividing the segment lies between the two points. If point P divides the segment joining A and B in the ratio m:n, this means that point P is located on the line segment connecting A to B, rather than outside the segment. This is important in three-dimensional geometry because it helps in determining the precise location of the dividing point within the specified parameters.
Examples & Analogies
Imagine a road trip where you stop at a rest area between your home and another city. If you and your friend are traveling and decide to meet at the 3/5 mark of your journey, you can think of the section formula as telling you where to pull over. You're both still on the path between the two locations, rather than having to go back or take a different route.
Applying the Section Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To apply the three-dimensional section formula, we can determine the coordinates of point P using the coordinates of points A and B and the given ratio.
Detailed Explanation
To calculate the coordinates of point P that divides the segment AB in the ratio m:n, we use the formula: P = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n), (mz2 + nz1) / (m + n)). Here, (x1, y1, z1) and (x2, y2, z2) are the coordinates of points A and B respectively, and m and n are the respective parts of the ratio. Each part of the formula corresponds to finding the average based on how much 'weight' each point has in defining the location of P.
Examples & Analogies
Think about making a smoothie with two different fruits β bananas and strawberries. If you decide to use 2 bananas and 3 strawberries for your smoothie, the section formula helps you determine how much of each fruit contributes to the final taste. The bananas' and strawberries' 'weights' in the smoothie will dictate how sweet or tangy the final result will be, similar to how the ratio m:n affects where point P is located between points A and B.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Section Formula: A formula to find coordinates of a point dividing a segment in a certain ratio.
-
Coordinates: Representation of a point in 3D space as (x, y, z).
-
Ratio: The division of segment lengths into parts in a specific proportion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given points P(1, 2, 3) and Q(4, 5, 6) that R divides in the ratio 2:3, find R's coordinates.
-
If A(2,3,4) and B(5,7,8) are two corners of a box, find the coordinates of the point that divides AB in the ratio 1:1.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the mid of points in 3D space, use section formula, itβs a strong base.
π Fascinating Stories
-
Imagine a treasure map! The pirate marks two islands (P and Q), and only by knowing the ratio of his travels can he find the hidden treasure at point R.
π§ Other Memory Gems
-
R-P-Q for remembering the segment points: Ratio-P1-P2-Coordinates.
π― Super Acronyms
SPARC
- Section formula
- Points
- Area
- Ratio
- Coordinates.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Section Formula
Definition:
A formula that provides the coordinates of a point dividing a line segment between two points in a specified ratio.
-
Term: Coordinates
Definition:
A set of values that show the position of a point in space with respect to the axes.
-
Term: Ratio
Definition:
A relationship between two numbers, indicating how many times the first number contains the second.