Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Three-Dimensional Geometry
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome class! Today we are starting three-dimensional geometry. Can anyone tell me what geometry typically involves?
Geometry deals with shapes and figures in a plane!
Exactly! But three-dimensional geometry takes this a step further by introducing a third dimension. We now have to consider points not just on a flat surface but in space. Can anyone guess what this third coordinate is?
Is it the z-coordinate?
Yes! We represent points in space using coordinates (x, y, z). This allows us to define locations in three-dimensional space. Remember the acronym XYZ for easy recall!
That makes sense! So, how does this apply to real life?
Great question! Understanding these concepts helps in fields like architecture and engineering where spatial awareness is crucial. Let's recap: we learned that three-dimensional geometry uses three coordinates to locate points in space.
Significance of 3D Geometry
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, why do you think three-dimensional geometry is important in various fields?
It must be important for designing buildings or models!
Exactly! Architects use these concepts to create accurate building models. Can someone think of other professions that use 3D geometry?
What about game development? They create 3D worlds!
Yes! Video game designers and animators also rely heavily on three-dimensional geometry. This underscores the relevance of what we're learning! Let's summarize: mastering these spatial concepts is essential across many industries.
Comparison with 2D Geometry
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Before we conclude, letβs compare two-dimensional geometry with three-dimensional geometry. Whatβs the main difference?
In 2D, we only need x and y coordinates!
Correct! In 3D, we need the z-coordinate. This addition allows us to describe positions in space more accurately. Does anyone remember how we find distances in three dimensions?
Is there a formula like the Pythagorean theorem?
Right! The distance formula in three dimensions extends the Pythagorean theorem, incorporating all three coordinates. To recap, weβve learned how crucial the third dimension is for representing points accurately in space.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces three-dimensional geometry, detailing how figures in space are represented using three coordinates. It emphasizes its importance in understanding shapes, distances, and directions beyond two dimensions.
Detailed
Detailed Summary of Introduction to Three-Dimensional Geometry
This section introduces the fundamental concepts of three-dimensional geometry, a vital extension of two-dimensional geometry into spatial dimensions. Unlike basic plane geometry, which operates using two coordinates (x and y), three-dimensional geometry employs a third coordinate (z) to describe a point's position within a three-dimensional space. This extension is crucial for analyzing distances, spatial relationships, and geometrical figures that cannot be represented on a flat surface.
The implications of mastering these concepts extend into advanced fields such as engineering, physics, computer graphics, and architecture, where spatial reasoning is essential. Understanding how to manipulate and visualize three-dimensional figures helps in comprehending not just the shapes but also their relationships and transformations in space.
Youtube Videos
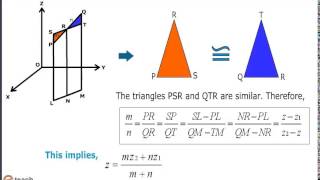
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Three-Dimensional Geometry
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Three-dimensional geometry studies figures in space using three coordinates.
Detailed Explanation
Three-dimensional geometry is the branch of mathematics that deals with shapes and figures that have depth, in addition to height and width. Unlike two-dimensional geometry, which only considers flat shapes on a plane (like squares and circles), three-dimensional geometry helps us understand how these shapes exist in space. We represent positions in this space using three coordinates: x, y, and z, which correspond to movements along the horizontal, vertical, and depth axes respectively.
Examples & Analogies
Think of a game of Minecraft, where you can move left and right (x-axis), up and down (y-axis), and also jump higher or go lower (z-axis). Every block you can place or stand on in the game can be described using three coordinates, just like in three-dimensional geometry.
Importance of Three Dimensions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It provides tools to analyze shapes, distances, and directions beyond the two-dimensional plane.
Detailed Explanation
The study of three-dimensional geometry is crucial for various practical applications. It allows us to calculate distances between objects in space, determine their orientations, and understand how they relate to each other spatially. For example, in architecture, three-dimensional geometry is used to create building designs that are both aesthetically pleasing and structurally sound. Similarly, in computer graphics and gaming, it helps in rendering realistic environments and character models.
Examples & Analogies
Imagine trying to build a model of a house. If you only had a flat drawing (2D), you couldn't figure out how tall the house is or how deep the rooms are. But with three-dimensional geometry, you can visualize all aspects of the house, including height, width, and depth, which are essential for accurate construction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Three-Dimensional Geometry: The study of geometric figures in three-dimensional space.
-
Coordinates System: The method of determining the position of a point using x, y, and z values.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A point represented as (2, 3, 5) indicates its position on the x-axis at 2, the y-axis at 3, and the z-axis at 5.
-
In architecture, understanding the dimensions (like height) is crucial for accurate building designs.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In three-dimensional space, we find, coordinates three; x, y, z, intertwined.
π Fascinating Stories
-
Imagine a 3D artist with a canvas of space; x, y, and z are the tools they trace.
π§ Other Memory Gems
-
Remember XYZ as the key to visualize the depth.
π― Super Acronyms
Remember the acronym POD
- Position must Define (for the three coordinates).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: ThreeDimensional Geometry
Definition:
A branch of mathematics that deals with shapes and figures in three-dimensional space using three coordinates.
-
Term: Coordinates
Definition:
A set of values that show an exact position in a space (e.g., (x, y, z) in 3D).