Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damping Ratio
Unlock Audio Lesson
Today, we're discussing the damping ratio, which is critical in analyzing how systems behave under dynamic loads. Can anyone tell me what damping ratio represents?
Is it how quickly a system returns to equilibrium?
Exactly, the damping ratio helps us understand the oscillatory motion and decay of those oscillations. It’s defined as ζ = c / (2√(mk)). Can anyone break down what each component represents?
c is the damping coefficient, m is mass, and k is stiffness.
Correct! If ζ is less than 1, the system is underdamped. This means not only will it oscillate, but it will do so with decreasing amplitude over time. The general solution will look like this... [writing on board]
Can you remind us what the general form is?
Of course! The general solution is y(t) = e^(-ζω_nt)(C cos(ω_d t) + C sin(ω_d t)). Here’s a mnemonic: 'Eager Cows Can Sing' to remember the structure of the equation. E = exponential decay, C = cosine, C = sine.
That’s a fun way to remember it!
Alright! Let's not forget, this model is extremely useful when designing buildings to withstand forces like earthquakes.
Natural Frequency Calculation
Unlock Audio Lesson
Next, let’s move on to natural frequency. Who remembers how we calculate the natural frequency, ω_n?
Is it ω_n = √(k/m)?
Yes! That’s spot on. Why is natural frequency important in engineering?
It helps predict how fast a system will respond to changes?
Exactly! Also, consider the damped frequency, ω_d, which tells us the adjusted frequency when damping is involved. Can anyone recall how to calculate it?
It’s ω_d = ω_n√(1 - ζ²).
Correct again! Let’s do a quick exercise. If we have m = 500 kg and k = 20000 N/m, what would be ω_n?
It would be √(20000/500) = √40 = 6.32 rad/s.
Great job! Now let's calculate ω_d using ζ = 0.354 from our example. Who can do that?
Application of Damping Ratio in Civil Engineering
Unlock Audio Lesson
Now that we’ve covered the theory, how does the damping ratio apply in civil engineering?
It helps engineers design structures to handle dynamic forces, right?
Correct! Buildings subjected to vibrations need to return to equilibrium quickly to remain safe. Can anyone provide an example where this is critical?
During earthquakes, buildings need to be stable to avoid collapse.
Absolutely! An underdamped system helps ensure oscillations decrease over time, which stabilizes structures. This process leads us to evaluate damping techniques used in skyscrapers and bridges!
Can you tell us more about those techniques?
Sure! Many tall buildings use tuned mass dampers to control their natural frequency, preventing excessive sway in high winds. Can anyone think of a famous example?
Burj Khalifa uses those, right?
Yes! And that’s how understanding damping ratios is crucial for safety and design in civil engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the definitions and calculations of the damping ratio and natural frequency in the context of engineering systems. It covers the implications of different damping ratios on system behavior and provides examples to illustrate their application in civil engineering.
Detailed
Damping Ratio and Natural Frequency
The damping ratio (B6) is a key parameter in the analysis of dynamic systems, particularly in civil engineering, where it defines how oscillations in a system decay over time due to damping. The damping ratio is calculated as:
a) B6 = c / (2√(mk))
Where:
- c = damping coefficient
- m = mass
- k = stiffness
When B6 < 1, the system is said to be underdamped and exhibits oscillatory behavior characterized by complex roots in the system's equation. The general solution for an underdamped system can be expressed as:
b) y(t) = e^(-B6ω_nt)(C_cos(ω_d t) + C_sin(ω_d t))
Where:
- ω_n = natural frequency = √(k/m)
- ω_d = damped frequency = ω_n√(1 - B6^2)
In a practical example involving a damped floor slab system, with given values of mass (m), damping coefficient (c), and stiffness (k), we can calculate the natural frequency and damping ratio. For instance:
- m = 500 kg
- c = 100 Ns/m
- k = 20000 N/m
Outputs:
- ω_n = 6.32 rad/s
- B6 = 0.354 (indicating underdamped behavior)
- ω_d = 5.9 rad/s
These calculations provide insight into the speed and smoothness with which the system returns to equilibrium after a disturbance.
Youtube Videos
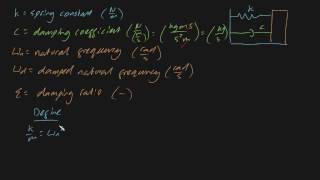
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Damping Ratio
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Damping Ratio ζ
ζ = \( \frac{c}{\sqrt{2mk}} \)
• If ζ < 1, the system is underdamped and exhibits oscillatory motion (complex roots).
Detailed Explanation
The damping ratio (ζ) is a measure of how oscillations in a system decay after a disturbance. It is calculated using the formula ζ = c / √(2mk), where 'c' is the damping coefficient, 'm' is the mass, and 'k' is the stiffness of the system. When ζ is less than 1, the system is characterized as 'underdamped', meaning it will oscillate before settling to equilibrium. This occurs because the strength of the damping is not sufficient to bring the system to a stable state immediately, allowing for periodic motion.
Examples & Analogies
Imagine pushing a child on a swing. If you give them a gentle push (low damping), they will swing back and forth several times before coming to rest. This is similar to an underdamped system where it oscillates multiple times before reaching a stable position.
Natural and Damped Frequency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• The general solution:
y(t) = e^(-ζω_n t)(C cos(ω_d t) + C sin(ω_d t))
Where:
• ω_n = \( \sqrt{\frac{k}{m}} \) = Natural frequency
• ω_d = ω_n √(1 - ζ²) = Damped frequency.
Detailed Explanation
The general solution of the motion can be expressed by the equation y(t) = e^(-ζω_n t)(C cos(ω_d t) + C sin(ω_d t)). The term ω_n (natural frequency) is calculated as the square root of the stiffness (k) divided by the mass (m). The damped frequency (ω_d) is obtained from the natural frequency adjusted by the damping ratio. Understanding these frequencies is critical because they describe how quickly the system oscillates and how swiftly these oscillations decay, ultimately informing engineers about the system's response over time.
Examples & Analogies
Think of a car on a bumpy road. The natural frequency (ω_n) would be how fast the car 'naturally' bounces based on how stiff the suspension is and how heavy the car is. If you've added too many passengers (increased mass), it may bounce differently. The damped frequency (ω_d) represents how long it takes for the car to stop bouncing around after going over a speed bump due to the shock absorbers (damping).
Civil Engineering Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a damped floor slab system:
• m = 500 kg
• c = 100 Ns/m
• k = 20000 N/m
We calculate:
• ω_n = 6.32 rad/s
• ζ = 0.354 (underdamped)
• ω_d = 5.9 rad/s
This gives insight into how quickly and smoothly the floor returns to equilibrium after a disturbance.
Detailed Explanation
In this example, we have a damped floor slab system with given values for mass (m), damping coefficient (c), and stiffness (k). By substituting these values into the formulas, we calculate the natural frequency (ω_n) as approximately 6.32 rad/s and the damping ratio (ζ) as 0.354, indicating that the system is underdamped. We further compute the damped frequency (ω_d) as 5.9 rad/s. These calculations indicate how quickly the floor slab will return to its resting position after a load is applied (like people moving across it), providing essential data for engineers to ensure structural safety and comfort.
Examples & Analogies
Imagine a trampoline (the floor slab) where people are jumping (the mass). If the trampoline is stiff (high k), it will bounce a lot, which is similar to a high natural frequency. If the springs in the trampoline aren't too strong (lower c), it takes a while for the bouncing to stop completely, just like how an underdamped system oscillates. Engineers need to find a balance so that the trampoline feels comfortable, but also doesn't bounce excessively after the jumpers land.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping Ratio (ζ): A measure that indicates how quickly oscillations decay in a damped system.
-
Natural Frequency (ω_n): The frequency at which a system naturally oscillates without damping.
-
Damped Frequency (ω_d): The frequency at which a damped system oscillates, typically less than the natural frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a damped structure like a floor slab with m = 500 kg, c = 100 Ns/m, and k = 20000 N/m, the natural frequency is ω_n = 6.32 rad/s, suggesting a specific response characteristic to excitations.
-
In a real-world scenario, if an earthquake shakes a building, understanding both the damping ratio and natural frequency helps engineers make crucial design decisions to ensure stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a ratio where dampness is low, oscillations will surely show; they bounce and sway, but over time decay, ensuring stability helps us know.
📖 Fascinating Stories
-
Imagine a bridge swaying in the wind. If its damping ratio is low, the movements might be graceful but risky. Engineers work to ensure that each bounce decreases with time, making the structure safe for everyone.
🧠 Other Memory Gems
-
Remember 'Dampening Natural Singers' to recall the damping ratio (D) and natural frequency (N) relationship in systems as they oscillate.
🎯 Super Acronyms
D.R.N.F - Damping Ratio, Natural Frequency
- Key terms for dynamic systems everyone needs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping Ratio (ζ)
Definition:
A dimensionless measure that describes how oscillations in a system decay over time due to damping.
-
Term: Natural Frequency (ω_n)
Definition:
The frequency at which a system oscillates when not subjected to damping or external forces.
-
Term: Damped Frequency (ω_d)
Definition:
The frequency of oscillation in a damped system, which is less than the natural frequency.
-
Term: Exponential Decay
Definition:
A process where the amplitude of oscillations decreases exponentially over time.
-
Term: Complex Roots
Definition:
Roots of the characteristic equation that indicate oscillatory behavior in systems.