Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Angular Acceleration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about angular acceleration. Can anyone tell me what acceleration means in general?
Acceleration is the rate of change of velocity.
Exactly! Now, when we talk about angular acceleration, what do you think we measure it with?
Maybe it's about the change in angular velocity?
Correct! Angular acceleration is the rate at which angular velocity changes over time. We can express it as \( \alpha = \frac{d\omega}{dt} \). Does anyone know what \( \omega \) represents?
It's the angular velocity!
Great! So, angular acceleration is related to how quickly the rate of rotation is increasing or decreasing.
Let's summarize: Angular acceleration measures how fast angular velocity changes over time.
Relationship with Torque
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's build on what we just learned about angular acceleration. How do you think it relates to torque?
Torque is what causes rotation, right? So it must influence angular acceleration.
Exactly! Torque is the rotational equivalent of force. We express the relationship as \( \tau = I \alpha \). Can anyone tell me what \( I \) stands for?
It's the moment of inertia!
Good! Moment of inertia is how mass is distributed relative to the axis of rotation. More mass further from the axis means a higher moment of inertia.
So, we have learned that the angular acceleration \( \alpha \), the torque \( \tau \), and the moment of inertia \( I \) are interlinked. If we apply a greater torque, we can expect a greater angular acceleration, provided the moment of inertia remains constant.
Real-Life Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's relate our discussion to real-life. Where do we see angular acceleration in action?
In vehicles during acceleration or deceleration!
Also in amusement rides that spin or rotate!
Exactly! In any case where a rotating object changes its speed, we're dealing with angular acceleration. It will help us understand how quickly something spins or slows down.
Always remember that every time you twist a knob on a door or accelerate in a vehicle, you're experiencing angular acceleration at work!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Angular acceleration is defined as the time rate of change of angular velocity. It can be represented in both scalar and vector forms. Understanding angular acceleration is crucial for analyzing rotational dynamics alongside torque and moment of inertia.
Detailed
Angular Acceleration in Rotational Motion
Angular acceleration is a critical concept in the study of rotational motion, defined as the rate of change of angular velocity over time. Mathematically, this can be expressed as:
$$\alpha = \frac{d\omega}{dt}$$
where \( \alpha \) is the angular acceleration and \( \omega \) is the angular velocity. In scenarios where the axis of rotation is fixed, the angular acceleration can also be expressed in scalar form as:
$$\frac{d}{dt} \omega = \alpha$$
Angular acceleration indicates how quickly an object is rotating and provides insights into its dynamic behavior when subjected to torques. The relationship between torque, moment of inertia, and angular acceleration is given by:
$$\tau = I \alpha$$
where \( \tau \) is the torque applied, and \( I \) is the moment of inertia of the object. Understanding angular acceleration is essential for analyzing the motion of rotating bodies, making it comparable to linear acceleration in translational motion.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Angular Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
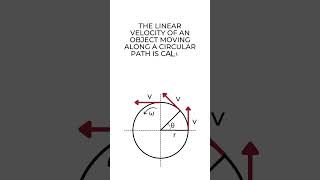
You may have noticed that we are developing the study of rotational motion along the lines of the study of translational motion with which we are already familiar. Analogous to the kinetic variables of linear displacement (s) and velocity (v) in translational motion, we have angular displacement (ΞΈ) and angular velocity (Ο) in rotational motion. It is then natural to define in rotational motion the concept of angular acceleration in analogy with linear acceleration defined as the time rate of change of velocity in translational motion. We define angular acceleration Ξ± as the time rate of change of angular velocity. Thus,
\[ d\omega = \alpha dt \quad (6.21) \]
If the axis of rotation is fixed, the direction of Ο and hence, that of Ξ± is fixed. In this case, the vector equation reduces to a scalar equation:
\[ \alpha = \frac{d\omega}{dt} \quad (6.22) \]
Detailed Explanation
Angular acceleration is essentially the rate at which the angular velocity of an object changes over time. If you picture a spinning wheel or a rotating disk, angular acceleration tells you how quickly it speeds up or slows down as it spins. The formula mentioned, dΟ = Ξ± dt, expresses this, indicating that the change in angular velocity (dΟ) can be related to the angular acceleration (Ξ±) multiplied by a small amount of time (dt). This is similar to how linear acceleration (the change of linear velocity over time) is defined in translational motion.
Examples & Analogies
Think about riding a bicycle. When you pedal harder, you accelerate, which means you're increasing your speed. If you apply the brakes, your speed decreases, which is equivalent to a negative acceleration. Now, when the bike is not only moving forward but you also lean into a turn, the way the bike spins around its axis is what we refer to as angular acceleration. Just like how your speed increases or decreases, the bike's angular velocity is changing as you lean more into the turn or straighten up.
Fixed Axis Consideration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the axis of rotation is fixed, the direction of Ο and hence, that of Ξ± is fixed. In this case, the vector equation reduces to a scalar equation:
\[ \alpha = \frac{d\omega}{dt} \quad (6.22) \]
Detailed Explanation
When considering fixed axes of rotation, it simplifies our analysis since both the angular velocity (Ο) and angular acceleration (Ξ±) keep a consistent direction. This means we don't need to worry about how they might change direction during motion, we only have to focus on their magnitudes and how they relate to time. This reduction to a scalar equation allows for easier calculations and helps us understand the dynamics of rotational motion more intuitively.
Examples & Analogies
Imagine a Ferris wheel. The central axis around which the wheel spins is fixed. We can measure how quickly the seats are moving as they spin (angular velocity) and how that speed increases or decreases with time (angular acceleration). Because the wheel rotates around that fixed vertical axis, we can easily predict the kind of increase or decrease in speed without worrying about any side-to-side movement. Just as the Ferris wheel must follow the path determined by its fixed axis, many rotational systems can be analyzed in a similar straightforward manner.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Angular acceleration as the rate of change of angular velocity.
-
Torque's influence on angular acceleration, defined by \( I\alpha = \tau \).
-
The significance of moment of inertia in rotational dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Adjusting the speed of a turntable demonstrates angular acceleration as the turntable's speed changes over time.
-
The rotation of a bicycle wheel shows how torque impacts angular velocity, particularly during acceleration.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Angular speed is quite wondrous, it spins around and never blunders.
π Fascinating Stories
-
Imagine a spinning dancer who speeds up as the music plays, but slows down when the song fades awayβthis illustrates angular acceleration beautifully.
π§ Other Memory Gems
-
For Torque and Angular, remember Ties Are Important, linking Torque (T), Angular acceleration (A), and Inertia (I)! (TAI).
π― Super Acronyms
Remember 'T.A.A.' for Torque, Angular Velocity, and Angular Acceleration.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Angular Acceleration
Definition:
The rate of change of angular velocity over time, represented as \( \alpha = \frac{d\omega}{dt} \).
-
Term: Angular Velocity
Definition:
The rate at which an object rotates, measured in radians per second.
-
Term: Torque
Definition:
A measure of the force causing an object to rotate, defined as \( \tau = r \times F \).
-
Term: Moment of Inertia
Definition:
A quantity expressing a body's tendency to resist angular acceleration, dependent on mass distribution.