Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Vector Product
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll discuss an important type of product known as the vector product or cross product. Can anyone tell me what they think this means?
Is it like multiplying numbers, but with vectors?
That's a good start! It's a way to combine two vectors to produce another vector. This new vector is perpendicular to the original two. Let's explore how we define it.
What do you mean by perpendicular?
Great question! When vectors are perpendicular, they meet at a right angle. This property is key in our understanding of the vector product.
Magnitude of the Vector Product
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The magnitude of the vector product |**c**| = |**a**| |**b**| sin(ΞΈ). Can someone tell me what each part of this means?
The |**a**| and |**b**| are the magnitudes of the vectors, right?
Exactly! And ΞΈ is the angle between the two vectors. The sine function helps us find the 'effectiveness' of the angle. Let's imagine two vectors at a 90-degree angle.
So, when they're at 90 degrees, sin(ΞΈ) = 1?
Yes! This maximizes the product, giving you the largest possible magnitude of the resulting vector.
Direction of the Vector Product
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about the direction of the vector product. Can anyone explain how we determine the direction using the right-hand rule?
You point your fingers from one vector to the other, then your thumb points up?
Exactly! When you curl your fingers from vector **a** to vector **b**, your thumb points in the direction of the resulting vector **c**.
What if I point my fingers the other way?
That would give you the opposite direction, which is why the product isn't commutative. Good catch!
Properties of the Vector Product
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's summarize some properties of the vector product. It does not change under reflection and is distributive over addition. Can someone describe what that means?
Under reflection, the direction reverses, right? But the product remains the same?
Exactly! It means that the result of the vector product doesn't depend on the direction of the vectors themselves. It just matters how they relate to each other.
Calculating the Vector Product
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's calculate the vector product of two vectors. If **a** = (3, 4, 5) and **b** = (2, 3, 1), how would we find **a** Γ **b**?
We can use the determinant method with i, j, and k!
Correct! Setting up the determinant helps us organize our calculations clearly. Let's run through the numbers together!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The vector product of two vectors is defined as a third vector that is perpendicular to the plane formed by the initial vectors. It can be calculated using magnitudes and the sine of the angle between them. The section discusses the right-hand rule for direction, non-commutativity of the product, and reflection properties.
Detailed
Detailed Summary
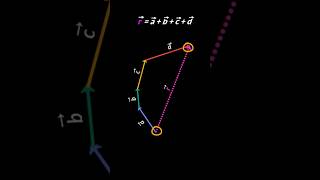
The vector product (or cross product) of two vectors, a and b, results in a new vector c, defined by three main properties:
- Magnitude: The magnitude of c is given by |c| = |a| |b| sin(ΞΈ), where ΞΈ is the angle between a and b.
- Direction: c is perpendicular to the plane defined by a and b. The right-hand rule can be used to determine the direction: if the fingers of the right hand follow the rotation from a to b, the extended thumb points in the direction of c.
- Non-commutativity: Unlike the scalar product, the vector product is not commutative; a Γ b is not equal to b Γ a and has the relationship a Γ b = -(b Γ a).
Additionally, the vector product is distributive over vector addition and does not change its sign under reflection. The section further explains the component method for calculating the vector product using determinants. Examples illustrate how to find both scalar and vector products.
Understanding the vector product is crucial for analyzing rotational quantities in physics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Vector Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are already familiar with vectors and their use in physics. In chapter 5 (Work, Energy, Power) we defined the scalar product of two vectors. An important physical quantity, work, is defined as a scalar product of two vector quantities, force and displacement.
Detailed Explanation
In this section, we introduce the concept of the vector product, which is different from the scalar product. While the scalar product results in a single quantity (a scalar), the vector product results in another vector. This distinction is crucial for understanding how different physical quantities interact, particularly in rotational motion.
Examples & Analogies
Think of the scalar product as finding out how much work you did when pushing a box across the floorβitβs a single measure of energy. In contrast, the vector product is like determining the direction of the torque when you twist a doorknob: it not only matters how much force you apply but also the direction in which you apply that force.
Definition of Vector Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A vector product of two vectors a and b is a vector c such that (i) magnitude of c = c sin(abΞΈ), where a and b are magnitudes of a and b and ΞΈ is the angle between the two vectors. (ii) c is perpendicular to the plane containing a and b. (iii) if we take a right handed screw with its head lying in the plane of a and b and the screw perpendicular to this plane, and if we turn the head in the direction from a to b, then the tip of the screw advances in the direction of c. This right handed screw rule is illustrated in Fig. 6.15a.
Detailed Explanation
The vector product (also called the cross product) defines a new vector that is perpendicular to both vectors involved in the operation. The magnitude of this vector product is determined by the sine of the angle between the two original vectors, emphasizing the role of direction in vector operations. This property is essential for calculating torque and angular momentum.
Examples & Analogies
Imagine using a screwdriver: the direction in which you turn the screwdriver (whether clockwise or counterclockwise) affects how it drives a screw into the wood. The right-hand screw rule illustrates this physical behavior where the direction of the resulting torque vector depends on the direction you turn the handle.
Properties of Vector Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Note that scalar product of two vectors is commutative as said earlier, a.b = b.a. The vector product, however, is not commutative, i.e., a Γ b β b Γ a. The magnitude of both a Γ b and b Γ a is the same (sin(abΞΈ)); also, both of them are perpendicular to the plane of a and b. But the rotation of the right-handed screw in the case of a Γ b is from a to b, whereas in the case of b Γ a it is from b to a. This means the two vectors are in opposite directions.
Detailed Explanation
The commutative property of the scalar product allows you to swap the order of the vectors without changing the result. However, for vector products, changing the order flips the direction of the resulting vector. This property is essential for understanding operations involving rotations and actions in physics. Furthermore, this section introduces the impact of reflection on vector products, which helps to understand how vectors behave under various transformations.
Examples & Analogies
This difference can be likened to two people pushing a cart in opposite directions: if they were to swap places, the direction of the movement would shift dramatically, resulting in a different outcome entirely. Understanding this helps when analyzing situations where forces and rotational effects are at play.
Vector Products in Component Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We may write c = a Γ b in the component form. For this we first need to obtain some elementary cross products: (i) a Γ a = 0 (0 is a null vector, i.e. a vector with zero magnitude). This follows since the magnitude of a Γ a is 2sin0 0aΒ° =. From this follow the results (i) i Γ i = 0, j Γ j = 0, k Γ k = 0. (ii) i Γ j = k. Note that the magnitude of i Γ j is sin90Β° or 1, since i and j both have unit magnitude and the angle between them is 90Β°.
Detailed Explanation
This chunk discusses how vector products can be expressed through their components. Understanding the specific relationships between unit vectors forms the basis for further calculations in physics. Knowing that the product of a vector with itself equals zero reflects an essential property of vectors that simplifies many calculations. Additionally, understanding the unit vectors and their relations aids in visualizing and solving 3D problems effectively.
Examples & Analogies
Think of the unit vectors as the basic colors of light; just as combining different colors gives rise to new ones, the interaction between these fundamental vectors forms the basis for constructing complex vector descriptions in physics.
Applications of Vector Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An interesting property of a vector product is its behavior under reflection. Under reflection (i.e. on taking the plane mirror image) we have, and, x x y y z zβ β β β β β. As a result, all the components of a vector change sign and thus, a β β b b β β. What happens to a Γ b under reflection? a Γ b β β Γ β = a Γ b. Thus, a Γ b does not change sign under reflection.
Detailed Explanation
The reflection property of vector products shows how these vectors respond to changes in their orientation. This behavior is crucial in physics, particularly in understanding forces and torque in various systems. By recognizing this property, students can better grasp how vectors interact with their surroundings, which connects to symmetry and conservation laws.
Examples & Analogies
Visualize looking in a mirror: as you raise one hand, your reflection mimics this action. Just as the vectors behave predictably under reflection, understanding these relationships aids in comprehending the fundamental principles governing the physical world.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Product: The process of combining two vectors to yield a third vector perpendicular to both.
-
Magnitude: Calculated as the product of the magnitudes of the vectors and the sine of the angle between them.
-
Right-Hand Rule: A technique to determine the direction of the resulting vector from the two original vectors.
-
Non-Commutativity: The concept that the vector product's outcome changes based on the order of the input vectors.
-
Distributive Property: The vector product can be distributed over addition of vectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given vectors a = (3, 4, 0) and b = (0, 0, 5), the vector product a Γ b yields (20, -15, 0).
-
If a = (1, 2, 3) and b = (4, 5, 6), then the cross product results in (-3, 6, -3).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When you cross vectors with a might, the result points to the right height!
π Fascinating Stories
-
Imagine two friends pushing a box. When they push at an angle, the box moves up in a new direction β this tells you about the vector product!
π§ Other Memory Gems
-
Use 'RIGHT' for the 'Right-Hand Rule' β Rotate, Index, Grip, Height!
π― Super Acronyms
CROSS β Calculate, Right-hand rule, Output vector, Sine of the angle, Sign changes!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Product
Definition:
A product of two vectors resulting in a new vector that is perpendicular to the plane formed by the two original vectors.
-
Term: Magnitude
Definition:
The length or size of a vector, measured as a non-negative value.
-
Term: Perpendicular
Definition:
When two lines or vectors intersect at an angle of 90 degrees.
-
Term: RightHand Rule
Definition:
A mnemonic used to determine the direction of the vector product, where the fingers curl from the first vector to the second.
-
Term: NonCommutativity
Definition:
A property indicating that the order of operations matters, as in vector products: a Γ b β b Γ a.
-
Term: Sin(ΞΈ)
Definition:
The ratio of the length of the opposite side to the hypotenuse in a right triangle, used here to determine components in the vector product.
-
Term: Determinant
Definition:
A mathematical object that can be calculated from the elements of a square matrix used here to find vector products.