Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Carnot Engine
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will learn about the Carnot engine, which is pivotal in thermodynamics. Can anyone tell me what they think makes an engine efficient?
I believe it depends on how well the engine converts heat into work without losing much energy.
Exactly! The Carnot engine is defined by its cycle which achieves maximum efficiency between two temperature reservoirs. Do you know who proposed this concept?
Was it Sadi Carnot?
Right! He established the Carnot theorem. This engine operates through a series of processes: two isothermal and two adiabatic processes. Let's examine each of these. What do we understand by an isothermal process?
Isothermal means that the temperature stays constant?
Great! During isothermal expansion, the gas absorbs heat from the hot reservoir at a constant temperature T1. When the gas expands, it does work. How does work relate to heat in the context of the Carnot engine?
Work is done by the gas while it absorbs heat in isothermal expansion?
Exactly! The work done equals the heat absorbed during this process. At the end of our session, letβs summarize today's key parts about the Carnot engine and its efficiency. Remember, it operates ideally between two thermal reservoirs, with efficiency defined as Ξ· = 1 - (T2/T1).
Carnot Cycle Processes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In this session, we will look closely at the four processes making up the Carnot cycle. The first process is isothermal expansion. Why is it crucial to keep the temperature constant?
Because it allows the system to absorb heat without changing temperature, helping maintain maximum efficiency!
Exactly! Now after the isothermal expansion, we undergo adiabatic expansion where the gas does work and reduces temperature. What happens to the internal energy of the gas during adiabatic expansion?
The internal energy decreases since the gas is doing work.
Correct! Next, the gas enters isothermal compression, where it releases heat to the cold reservoir at T2. What is unique about this process?
Itβs still isothermal, so the temperature is constant while the gas is being compressed?
Yes! This leads us to the final phase, adiabatic compression, where the gas is compressed and its temperature rises again. What do you notice about the entire cycle?
It just keeps going back to its initial state!
"Exactly! Thatβs what makes it a cycle. Remember, the essence of this efficiency comes down to keeping processes reversible, minimizing entropy.
Efficiency of the Carnot Engine
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Understanding the efficiency of the Carnot engine is crucial. What is the maximum efficiency formula we discussed?
Ξ· = 1 - (T2/T1)?
Very good! Now, why is it significant that this efficiency is independent of the working substance?
It implies that the engine's performance is purely based on the temperature difference!
Exactly! Also, the Carnot engine serves as a benchmark for other engines. How does this knowledge help engineers?
It helps them to design more efficient engines by striving to approach Carnot efficiency.
Absolutely! All real engines have less efficiency than the Carnot engine because they are not reversible. Letβs wrap up this key point: the Carnot engine provides essential insights and sets limits on what can be achieved in real systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Developed by Sadi Carnot, the Carnot engine theoretically optimizes efficiency by operating through two isothermal processes (absorbing and releasing heat) and two adiabatic processes (changing temperature without heat transfer). This section discusses the maximum efficiency of such engines, formulates the Carnot cycle, and emphasizes the relationship between temperature and efficiency.
Detailed
Detailed Summary of the Carnot Engine
The Carnot engine is an idealized thermodynamic engine that presents the maximum possible efficiency achievable when transferring heat from a hot reservoir to a cold reservoir. Sadi Carnot introduced this fundamental concept in 1824, establishing a framework that highlights the inefficiencies found in real-world engines and the concept of reversible processes.
Key Aspects of the Carnot Engine:
1. Efficiency and Its Formula: The efficiency of the Carnot engine is expressed as Ξ· = 1 - (T2/T1), where T1 is the temperature of the hot reservoir and T2 is that of the cold reservoir. This relation demonstrates that the efficiency is dependent only on the temperatures of the reservoirs, not on the working substance.
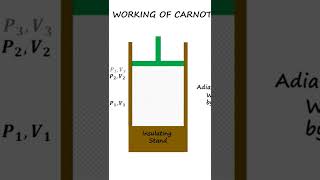
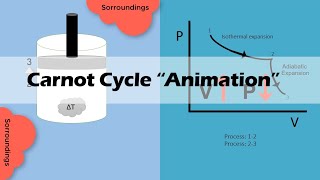
2. Carnot Cycle: The operation of the Carnot engine consists of four stages:
- Isothermal Expansion: The engine absorbs heat Q1 from the hot reservoir at constant temperature T1.
- Adiabatic Expansion: The gas expands, doing work on the surroundings while its temperature drops to T2.
- Isothermal Compression: The engine releases heat Q2 to the cold reservoir while remaining at T2.
- Adiabatic Compression: The gas is compressed, raising its temperature to T1, completing the cycle.
3. Real-world Applications: While actual heat engines cannot achieve Carnot efficiency due to irreversibility and dissipative effects, the Carnot engine serves as a benchmark for assessing performance and efficiency in thermodynamic systems.
Overall, the Carnot engine introduces essential principles of thermodynamics and offers critical insights into energy conversion, setting the foundation for future advancements in thermal systems.
Youtube Videos
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Carnot Efficiency: The formula Ξ· = 1 - (T2/T1) expresses the efficiency of a Carnot engine operating between two temperature reservoirs.
-
Carnot Cycle: It includes a series of four distinct processesβtwo isothermal and two adiabaticβthat cyclically return to the initial state.
-
Reversible Processes: The Carnot engine operates under processes that ideally have no dissipative effects, maximizing work output.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An ideal gas turbine working in a Carnot cycle can theoretically achieve efficiency based on the absolute temperatures of its reservoirs, illustrating the temperature dependency.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Carnot was wise, with temperature ties, maximizing heat into work, oh what a prize!
π Fascinating Stories
-
Imagine a machine in a perfect land, transforming heat into work with a gentle hand, in a cycle so smooth like the sun and sands.
π§ Other Memory Gems
-
Remember the steps: I(so thermal) Eagles soar (isothermal expansion) and Cold calories compress (isothermal compression).
π― Super Acronyms
C.E. = Carnot Efficiency (C for Carnot, E for Energy transfer).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Carnot Engine
Definition:
An idealized thermal engine that operates on a reversible cycle and establishes the maximum efficiency possible for converting heat into work between two thermal reservoirs.
-
Term: Isothermal Process
Definition:
A process that occurs at a constant temperature, allowing heat transfer without temperature change.
-
Term: Adiabatic Process
Definition:
A process in which no heat is exchanged with the surroundings, typically involving a change in temperature as work is done.
-
Term: Reversible Process
Definition:
A hypothetical process that, if reversed, would return the system and surroundings to their initial states without additional changes.
-
Term: Efficiency
Definition:
The ratio of useful work output to the heat input in a system, commonly expressed as a percentage.