Learn
Games

4.3.4 - The Profit Maximisation Problem: Graphical Representation

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Profit Maximisation in Graphical Form

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we will explore how firms maximise profits using graphical representation. Can anyone explain what we mean by profit maximisation?

Student 1
Student 1

I think it means producing the amount of goods that makes the most money or profit.

Teacher
Teacher

Exactly! Profit maximisation occurs when a firm's revenue exceeds its costs as much as possible. In a perfectly competitive market, this happens where the marginal cost equals the marginal revenue. Does anyone know why?

Student 2
Student 2

Because if you produce one more unit and it costs more than the revenue it brings, you lose money?

Teacher
Teacher

Precisely! This concept revolves around the equation MR = MC. We will see how this relationship plays out graphically.

Graphical Representation of Total Revenue and Costs

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let's look at how total revenue varies with different levels of output. Can someone explain what the total revenue curve looks like?

Student 3
Student 3

It’s a straight line because the price is constant in perfect competition, right?

Teacher
Teacher

Exactly! The total revenue rises as we increase output, forming a straight line graph. Now, what about total cost?

Student 4
Student 4

The total cost curve goes up more steeply, especially when more units are produced.

Teacher
Teacher

Correct! The area between total revenue and total cost represents profit. Can anyone summarise how we locate the profit maximisation point?

Student 1
Student 1

It’s where the total revenue curve is above the total cost curve, and the difference is the highest.

Teacher
Teacher

Great summary! Remember, at the profit maximising point, marginal revenue equals marginal cost too!

Conditions for Profit Maximisation

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

We've talked about MR = MC. Can anyone list the conditions that need to be met for a firm to maximise profits?

Student 2
Student 2

The price must equal marginal cost, and marginal cost needs to be non-decreasing.

Teacher
Teacher

Exactly! And what about the third condition?

Student 3
Student 3

The price has to be greater than the average variable cost in the short run?

Teacher
Teacher

Correct! These three conditions must hold for profit maximisation. Let’s ensure we keep these in mind as we move forward.

Graphical Representation of Profit Areas

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, let's focus on how to identify the profit area on our graphs. Who can explain how to determine this visually?

Student 4
Student 4

The profit area is the rectangle formed between total revenue and total cost curves?

Teacher
Teacher

Exactly! It’s the area where total revenue exceeds total cost. What happens if these curves meet?

Student 1
Student 1

Then the firm breaks even, with no profit.

Teacher
Teacher

Well said! Recognising this area helps in comprehending firm behaviour under perfect competition.

Key Insights and Recap

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

What have we covered regarding graphical representation and profit maximisation today?

Student 3
Student 3

We learned about how firms maximise profit by ensuring MR equals MC.

Student 2
Student 2

And how to graph total revenue and total cost for finding the profit area.

Student 4
Student 4

Also, the conditions for profit maximisation are critical to understand.

Teacher
Teacher

Fantastic recap! Let’s continue reinforcing these insights as we move ahead in our study of economics.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section explores the graphical representation of a firm's profit maximisation problem in the context of perfect competition.

Standard

The section explains how, under perfect competition, firms aim to produce at a level where their marginal cost equals the market price to maximise profits. It illustrates the relationship between total revenue and total cost graphically, highlighting key conditions for profit maximisation.

Detailed

In this section, we delve into the profit maximisation problem for firms operating under perfect competition by employing graphical representations. We begin by understanding that a firm's objective is to produce at an output level where marginal revenue (MR) equals marginal cost (MC). The graphical representation helps in visualising this relationship: the total revenue curve, which demonstrates a straight upward slope due to the constant market price, contrasts against the average cost curves. The area representing profit is highlighted as the difference between total revenue and total cost, facilitating a clearer understanding of how profits change with varying levels of output. We also discuss conditions under which profit maximisation occurs and how graphical analysis aids in determining the optimal output level for firms.

Youtube Videos

Profit maximization | APⓇ Microeconomics | Khan Academy
Profit maximization | APⓇ Microeconomics | Khan Academy
Perfect Competition Short Run (1 of 2)- Old Version
Perfect Competition Short Run (1 of 2)- Old Version
NCERT Class 12 Economics Chapter 4: Theory Of The Firm Under Perfect Competition | CBSE | English
NCERT Class 12 Economics Chapter 4: Theory Of The Firm Under Perfect Competition | CBSE | English
Profit maximization in Perfect competition | Why is MC=MR at the profit maximizing level of output?
Profit maximization in Perfect competition | Why is MC=MR at the profit maximizing level of output?
NCERT CLASS 12|MICROECONOMICS| CHAPTER-4|PROFIT MAXIMIZATION CONDITIONS|#36
NCERT CLASS 12|MICROECONOMICS| CHAPTER-4|PROFIT MAXIMIZATION CONDITIONS|#36
Profit Maximisation in Perfect Competition
Profit Maximisation in Perfect Competition
Class 11 Economics Chapter 4 | Perfect Competition | Profit Maximisation
Class 11 Economics Chapter 4 | Perfect Competition | Profit Maximisation
Economics Class 12 | Theory Of Firm Under Perfect Competition | Profit Maximization | NCERT | CBSE
Economics Class 12 | Theory Of Firm Under Perfect Competition | Profit Maximization | NCERT | CBSE
The Theory Of The Firm Under Perfect Competition 30 Minutes Revision | Class 11 Economics Chapter 4
The Theory Of The Firm Under Perfect Competition 30 Minutes Revision | Class 11 Economics Chapter 4
Y2 13) Perfect Competition
Y2 13) Perfect Competition

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Graphical Representation of Profit Maximisation

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

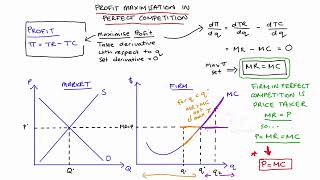
Using the material in sections 3.1, 3.2 and 3.3, let us graphically represent a firm’s profit maximisation problem in the short run. Consider Figure 4.6. Notice that the market price is p. Equating the market price with the (short run) marginal cost, we obtain the output level q₀. At q₀, observe that SMC slopes upwards and p exceeds AVC. Since the three conditions discussed in sections 3.1-3.3 are satisfied at q₀, we maintain that the profit-maximising output level of the firm is q₀.

Detailed Explanation

In this chunk, we are looking at how we can visualize the process by which a firm maximizes its profits. The graph essentially plots the relationship between price, marginal costs, and average variable costs. The firm will continue to produce as long as the price they receive for their product (p) is greater than their average variable costs (AVC) and marginal cost (MC) equals the price. If we draw the demand curve (which is horizontal for a price-taker) at price p and compare it with the marginal cost curve (which generally slopes upwards), we can find the quantity q₀ where these two curves intersect, showing the optimal output level for profit maximization. This is an important concept in economic theory because it shows firms will not produce if they cannot at least cover their variable costs, which is essential for staying in business in the short run.

Examples & Analogies

Think of a pizza shop deciding how many pizzas to make for the evening. The shop knows that it can sell pizzas at $10 each. They calculate their costs, and it turns out that the cost to make each additional pizza is $7. To maximize their profit, they will continue to make pizzas as long as they can sell them for $10 (which is greater than their $7 cost). If they reach a point where the cost to make another pizza exceeds $10, they will stop making more because they would be losing money. The graphically identified quantity (q₀) ensures they generate the highest profit under these conditions.

Understanding Revenue and Profit at Output Level

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

What happens at q₀? The total revenue of the firm at q₀ is the area of rectangle OpAq₀ (the product of price and quantity) while the total cost at q₀ is the area of rectangle OEBq₀ (the product of short run average cost and quantity). So, at q₀, the firm earns a profit equal to the area of the rectangle EpAB.

Detailed Explanation

In this chunk, we delve into the financial aspect of profit maximization. At the profit-maximizing output level (q₀), we can calculate the total revenue and total costs geometrically based on rectangular areas in the graph. Total revenue (TR) is calculated by multiplying the price (p) by the quantity sold (q₀), which represents the area of rectangle OpAq₀. On the other hand, total cost (TC) takes into account the average cost (AC) of production times the same quantity, giving us the area of rectangle OEBq₀. Profit is then derived by subtracting total costs from total revenues, visually represented as the area EpAB in the graph. Profit maximization occurs where this area is largest.

Examples & Analogies

Imagine the same pizza shop again. If the shop sells 15 pizzas at $10 each, their total revenue will be $150 (15 * $10). If it costs them $5 per pizza for ingredients and labor (amounting to $75 for 15 pizzas), they realize a profit of $75. In terms of our area metaphor, if the revenue rectangle is $150 and the cost rectangle is $75, the area that represents profit would be everything in between, coloring in a visual rectangle of size $75, signifying the shop's profit.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Marginal Cost: The cost of producing one additional unit.

  • Marginal Revenue: The revenue gained from selling one additional unit.

  • Total Revenue Curve: A straight line indicating total revenue based on output.

  • Profit Area: The space between the total revenue and total cost curves that indicates profit.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • If a firm has a market price of Rs 20 and produces 10 units at a total cost of Rs 150, its total revenue would be Rs 200, resulting in a profit of Rs 50.

  • When price equals MC at Rs 20, the firm maximises its profit by producing 10 units because producing more would incur higher costs than revenue gained.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To find where profit peaks, MR and MC must speak!

📖 Fascinating Stories

  • Imagine a baker who sells cookies at a fixed price. To maximise profit, she adjusts her production until the cost of baking one more cookie equals the price she receives. That’s how she knows she’s hit her sweet spot!

🧠 Other Memory Gems

  • P-MR-MC-PA: Profit-Maximising Requirement = Marginal Revenue = Marginal Cost = Profit Area.

🎯 Super Acronyms

TRAP

  • Total Revenue Above Costs = Profit maximisation.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Profit maximisation

    Definition:

    The process of determining the output level at which a firm achieves the highest possible profit.

  • Term: Marginal Cost (MC)

    Definition:

    The additional cost incurred from the production of one more unit.

  • Term: Marginal Revenue (MR)

    Definition:

    The additional revenue generated from the sale of one more unit.

  • Term: Total Revenue (TR)

    Definition:

    The total income generated from the sale of goods or services.

  • Term: Total Cost (TC)

    Definition:

    The total expenses incurred in the production of goods or services.