Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bohr's Model
Unlock Audio Lesson
Alright class, today we're diving into the Bohr model of the hydrogen atom. Can anyone tell me why we needed a new model after Rutherford's?
I think Rutherford's model couldn't explain why electrons don't just spiral into the nucleus.
Exactly! That's a key point. Rutherford's model suggested that because electrons are accelerating, they would lose energy and fall into the nucleus. But Bohr addressed this by proposing stable orbits. Can anyone explain what that means?
Does that mean electrons can stay in certain orbits without losing energy?
Correct! These stable orbits are called 'stationary states.' Now, how do we understand the energy associated with these states?
Isn't that related to the quantization of angular momentum?
Yes! And that's where Bohr's second postulate comes in. He stated that the angular momentum of the electron is quantized, meaning L = nh/2π. Can anyone tell me what this implies about the possible orbits?
Only certain orbits with discrete values for angular momentum are allowed!
Well done! Let's summarize: Bohr introduced the concept of stable orbits and quantized angular momentum, setting the stage for how we understand atomic structure today.
Energy Levels and Spectra
Unlock Audio Lesson
Now that we understand the stable orbits, let's discuss energy levels. How did Bohr quantify the energy of these orbits?
If I remember correctly, he showed that the energy is negative and dependent on the orbit number.
That's right! The energy for the nth level is given by E_n = -13.6 eV/n². What does this negative value indicate?
It means the electron is bound to the nucleus.
Exactly! Next question: what happens when an electron transitions from a higher energy level to a lower one?
A photon is emitted! The energy difference between the two levels is carried away by the photon.
Perfect! This leads us to the atomic spectra we observe. How do these transitions relate to the colors we see in spectra?
Each transition corresponds to specific wavelengths, right?
Exactly again! This is why we see discrete lines in the spectrum. Bohr's model does an excellent job explaining the spectral lines of hydrogen.
Limitation of Bohr's Model
Unlock Audio Lesson
We've seen how Bohr's model works, but it also has limitations. What are some of these limitations?
It only works for hydrogen and hydrogen-like atoms!
Correct! The model struggles with more complex atoms. What else?
It doesn't explain why different spectral lines have different intensities?
Great point! Spectral intensities depend on the transitions' probabilities, which Bohr's model does not address. What do you think would be the next steps for atomic theory?
Maybe moving towards quantum mechanics?
Exactly! Quantum mechanics will give us a more complete understanding, addressing many of these limitations. Let’s summarize: Bohr's model provided groundbreaking insights but also laid the groundwork for further development in atomic theory.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Proposed by Niels Bohr, this model revolutionizes the atomic concept by suggesting that electrons occupy quantized orbits around the nucleus, where they can move without radiating energy. This model explains the discrete spectral lines observed in hydrogen and introduces the idea of quantized angular momentum.
Detailed
Bohr Model of the Hydrogen Atom
The Bohr model of the hydrogen atom emerged as a critical development in atomic theory after the Rutherford model. While Rutherford's model suggested that electrons spiral into the nucleus due to electromagnetic radiation emitted during acceleration, Bohr's model provided stability through quantization. This key idea posited that electrons occupy certain stable orbits without radiating energy and that the angular momentum of these orbits is quantized.
Key Features of Bohr's Model:
- Stable Orbits: Electrons can revolve in specified orbits or stationary states, avoiding energy loss traditionally attributed to accelerating charges.
- Quantized Angular Momentum: The angular momentum of an electron in the nth orbit is quantized, described by the equation L = nh/2π, where n is an integer. This quantization prevents the electron from spiraling into the nucleus.
- Energy Levels: The total energy of an electron in these orbits is also quantized, leading to discrete energy levels, with the energy of the nth level given by E_n = -13.6 eV/n².
- Hydrogen Spectrum: Only when an electron transitions between these defined levels does it emit or absorb photons, explaining the discrete emission and absorption spectra observed.
Ultimately, while Niels Bohr's model successfully explained several features of atomic spectra and introduced vital quantum concepts, it was limited to hydrogen-like atoms and faced challenges in accounting for spectral intensity variations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bohr Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The model of the atom proposed by Rutherford assumes that the atom, consisting of a central nucleus and revolving electron is stable much like sun-planet system which the model imitates. However, there are some fundamental differences between the two situations.
Detailed Explanation
In this chunk, we introduce the Bohr model, highlighting that it builds upon the Rutherford model which depicted the atom as having a nucleus at its center with electrons revolving around it, akin to planets orbiting the sun. Yet, the Bohr model acknowledges the discrepancies between gravitational forces in a solar system and the electromagnetic forces that operate in an atom. This sets the stage for a deeper exploration into why the Bohr model was necessary.
Examples & Analogies
Think of the difference as similar to a merry-go-round (Rutherford model) versus a roller coaster (Bohr model). On a merry-go-round, riders are securely attached, like electrons in certain orbits. The roller coaster’s twists and turns reflect the more complex interactions of forces in an atom where stability must be achieved despite radical acceleration.
Challenges of Classical Electromagnetic Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
While the planetary system is held by gravitational force, the nucleus-electron system being charged objects, interact by Coulomb’s Law of force. We know that an object which moves in a circle is being constantly accelerated – the acceleration being centripetal in nature. According to classical electromagnetic theory, an accelerating charged particle emits radiation in the form of electromagnetic waves.
Detailed Explanation
In Newtonian physics, if an electron (charged particle) moves in a circular path, it must constantly accelerate towards the center. Classical electromagnetic theory suggests that this acceleration should cause the electron to emit energy as electromagnetic radiation, causing it to lose energy and spiral into the nucleus. This presents a contradiction: if this were true, atoms couldn't be stable, which is contrary to observations.
Examples & Analogies
Imagine a child on a swing who keeps pushing away to maintain height. If the child didn’t exert effort (energy), they would descend into the ground. Similarly, if electrons lose energy and spiral inward, they cannot maintain stable orbits.
Bohr's Modifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It was Niels Bohr (1885 – 1962) who made certain modifications in this model by adding the ideas of the newly developing quantum hypothesis. Niels Bohr studied in Rutherford’s laboratory for several months in 1912 and he was convinced about the validity of Rutherford nuclear model.
Detailed Explanation
Bohr proposed three postulates that modified the Rutherford model to incorporate quantum mechanics. The first postulate suggests that electrons can only exist in certain stable orbits without radiating energy, unlike classical predictions. The second postulate quantizes angular momentum, making it an integral multiple of 'h/2π'. Finally, the third postulate introduces the concept of energy transitions between these orbits, where photons are emitted or absorbed.
Examples & Analogies
Think of Bohr's adjustments as tuning a musical instrument. Just like a guitar string vibrates at specific frequencies to create distinct notes, electrons occupy specific energy states, and transitions between these states emit particular frequencies of light.
Bohr's Postulates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Bohr combined classical and early quantum concepts and gave his theory in the form of three postulates. These are: (i) An electron in an atom could revolve in certain stable orbits without the emission of radiant energy.
Detailed Explanation
Bohr's first postulate states that electrons can occupy specific, stable orbits without losing energy. This revolutionary idea was crucial because it explained why atoms remained stable while still allowing for transitions that involve energy changes. His second postulate quantizes angular momentum, suggesting that only certain values are allowed, reinforcing stability. Lastly, the third postulate defines how energy transitions occur.
Examples & Analogies
Consider a roller coaster where only certain tracks are usable. Similar to how riders only exist in certain tracks at levels without crashing, electrons occupy stable orbits and only transition when they gain or lose energy.
Implications of Bohr's Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The energy of an atom is the least (largest negative value) when its electron is revolving in an orbit closest to the nucleus i.e., the one for which n = 1. The lowest state of the atom, called the ground state, is that of the lowest energy.
Detailed Explanation
In Bohr's model, the ground state corresponds to the electron being in its lowest energy level (n=1). This state is crucial because it defines the atom's stability and energy requirements for ionization. For hydrogen, 13.6 eV is needed to remove the electron from the ground state. Higher orbits (n > 1) represent excited states, which require additional energy to reach and can emit energy when returning to the ground state.
Examples & Analogies
Think of a child in a treehouse. The lower they are (n=1), the easier it is to stay there without much effort. They require more energy to climb higher (excited states), and when they slide back down, they release energy, much like the electron releasing a photon.
Limitations of Bohr's Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
However, Bohr’s model is applicable only to hydrogenic (single electron) atoms. It cannot be extended to even two electron atoms such as helium. This model is also unable to explain for the relative intensities of the frequencies emitted even by hydrogenic atoms.
Detailed Explanation
While Bohr's model significantly enhances our understanding of hydrogen's spectral lines, it has limitations. It fails to address the interactions in multi-electron atoms and does not explain why certain transitions emit stronger light than others in hydrogen. As a result, more advanced quantum mechanics is needed for these cases.
Examples & Analogies
Imagine trying to use a simple map for a complex city; its limitations become apparent as interactions and routes increase in complexity. Similarly, while Bohr's model is useful, it cannot account for the complexities arising in atoms with more than one electron.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Bohr Model: A theory that introduces quantized orbits for electrons in hydrogen atomic structure.
-
Electron Transition: Movement of an electron between energy levels, emitting or absorbing a photon.
-
Quantization of Angular Momentum: The assertion that the angular momentum of an electron is quantized, leading to discrete orbits.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The hydrogen atom's ground state energy is -13.6 eV, where the electron is in the closest orbit to the nucleus.
-
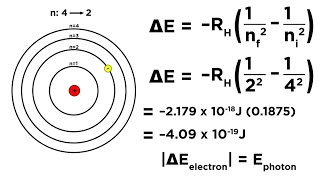
When an electron transitions from n=2 to n=1, a photon with energy equal to the difference in these states is emitted.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In orbits round they spiral, electrons with no trial, emit not a single ray, in Bohr's light, they play.
📖 Fascinating Stories
-
Imagine electrons as dancers on a stage, twirling in perfect orbits without losing energy, knowing the rhythm of their quantized moves.
🧠 Other Memory Gems
-
Remember 'SNAP' for Bohr: Stable orbits, Negative energy, Angular momentum quantization, Photon absorption/emission.
🎯 Super Acronyms
USE 'BASE' to remember Bohr's contributions
- B- Bound states
- A- Angular momentum
- S- Stable orbits
- E- Energy levels.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quantum
Definition:
The minimum amount of any physical entity involved in an interaction.
-
Term: Stationary State
Definition:
An orbit in which an electron can revolve around the nucleus without emitting energy.
-
Term: Angular Momentum
Definition:
The momentum associated with an object rotating around an axis.
-
Term: Discrete Spectrum
Definition:
A spectrum that consists of specific wavelengths emitted or absorbed by an atom.