Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're starting with the Fast Fourier Transform, or FFT for short. Can anyone tell me what they remember about the Discrete Fourier Transform?
Isn't it used to convert a signal from the time domain to the frequency domain?
Exactly! The DFT does just that. However, direct computation of the DFT is very inefficient. This is where the FFT comes in.
So, how does the FFT make it faster?
Great question! The FFT reduces the number of calculations from O(NΒ²) to O(N log N) through a method called 'divide-and-conquer.' Can anyone remember why reductions in calculations are important in real-time applications?
Because they allow us to process larger datasets more quickly!
Exactly right! Now let's outline our journey into how the FFT works and where we can apply it.
How FFT Works
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The FFT algorithm uses a divide-and-conquer strategy. To illustrate, it divides the input signal into even and odd indexed samples. Can someone explain what this means?
You split the signal into two smaller parts based on their positions!
Correct! After that, you compute the DFT for these smaller sections recursively. Why do you think this helps?
It simplifies the problem into smaller, more manageable pieces!
Right again! We can also think of it as building blocks that combine the results to make the larger DFT easy to compute. This is what makes the FFT both efficient and powerful.
Example of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's work through a simple example of computing an 8-point DFT using FFT. Who can tell me what happens in the first step?
We would divide it into smaller DFTs, starting with two groups of four.
Exactly! And then what comes next after that?
Each 4-point DFT gets divided further into 2-point DFTs!
Great! This process continues until we reach manageable sizes. By combining all these results, we can effectively reduce our computation time. What could be a real-world application for using FFT?
Perhaps in audio processing, to analyze sound waves!
Absolutely, that's one of the prominent uses of FFT!
Applications of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
We now see how the FFT is applied. Can anyone list some of the fields that benefit from FFT?
Audio and image processing!
And communication systems, right?
Exactly, as well as in medical imaging and radar systems! Each of these fields relies on the ability to analyze vast amounts of data rapidly. Remember the FFTβs importance in making real-time processes viable.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Fast Fourier Transform (FFT) is an algorithm that dramatically improves the efficiency of DFT computations, decreasing the required operations from O(NΒ²) to O(N log N). This efficiency makes FFT suitable for real-time processing in a variety of applications ranging from audio and image processing to communications.
Detailed
The Fast Fourier Transform (FFT) is a pivotal algorithm that enhances frequency analysis by efficiently computing the Discrete Fourier Transform (DFT). The DFT, essential for transforming time-domain signals into the frequency domain, requires O(NΒ²) operations for direct computation. However, the FFT algorithm reduces this to O(N log N) through a divide-and-conquer strategy. By breaking the computation down into smaller DFTs recursively and exploiting symmetries, particularly in the Cooley-Tukey Radix-2 FFT implementation, the FFT facilitates quicker processing of large sets of data. This capacity makes it invaluable in various real-time applications such as audio analysis, image processing, speech recognition, and more.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Fast Fourier Transform (FFT) is an algorithm designed to efficiently compute the DFT. The direct computation of the DFT from the formula involves O(N^2) operations, which becomes computationally expensive for large values of N. The FFT reduces this complexity to O(N log N), making it much faster and more suitable for real-time applications.
Detailed Explanation
The FFT is essentially a method to perform the Discrete Fourier Transform (DFT) calculations more efficiently. The standard DFT calculation involves a lot of operations, specifically O(N^2), meaning that if you double the number of data points, the time it takes to compute the DFT quadruples. In contrast, the FFT algorithm reduces that time significantly to O(N log N), which allows for practical and faster computations, such as analyzing audio or video signals in real-time.
Examples & Analogies
Imagine trying to organize a large library of books. If you check every book against every other book (an O(N^2) task), it could take forever as the library grows. However, if you use an efficient sorting strategy, such as dividing the books into smaller sections and sorting those, you can accomplish the task much faster (akin to O(N log N)). This efficiency is what the FFT brings to signal processing.
How FFT Works
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The FFT algorithm is based on the divide-and-conquer approach. It recursively divides the DFT computation into smaller DFTs, exploiting symmetries in the DFT formula. The most common implementation of the FFT is the Cooley-Tukey Radix-2 FFT algorithm, which works efficiently when the number of samples N is a power of 2.
Detailed Explanation
In the FFT algorithm, we use a method called 'divide-and-conquer'. This means we break down the larger problem of computing the DFT into smaller, more manageable problems. For instance, if you have 8 data points, instead of calculating the DFT directly, the algorithm splits this into two groups of 4 and then further divides those down to 2 points. By cleverly combining these smaller results, we can compute the DFT fast. The Radix-2 algorithm is one specific way to do this, typically used when the number of samples is a power of 2 (like 2, 4, 8, etc.).
Examples & Analogies
Think of it like building a large jigsaw puzzle. Instead of working on the whole puzzle at once, you can separate the pieces into smaller sections (like corners and edge pieces) and complete those first. Once the smaller sections are done, you can combine them to finish the puzzle. This is how FFT efficiently computes large DFTs by working with smaller parts.
Example of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
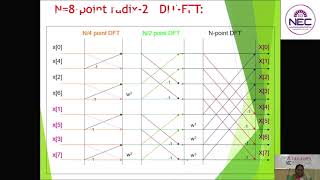
Consider a simple example of an N=8 point DFT computation. Instead of computing the DFT directly from the definition, the FFT algorithm would divide the 8-point DFT into smaller 4-point DFTs, and each 4-point DFT would be further divided into 2-point DFTs. This recursive process reduces the number of operations significantly.
Detailed Explanation
Using an example of 8 data points (N=8), instead of calculating all pairs directly (which would take O(8^2) = 64 operations), the FFT breaks this into two groups of 4 points, which are further divided into 2-point groups. Each smaller DFT requires fewer operations, and by combining these results, FFT efficiently computes the DFT with only O(8 log 8) operations. Thus, the total time taken becomes much shorter.
Examples & Analogies
Imagine you are trying to taste-test different flavors of ice cream. If you try each ice cream flavor with every other flavor, it would take a long time. However, if you divide them into groups (like cones, cups, and toppings) and taste each group in smaller batches before combining your favorites, you can narrow down your choice much faster. This approach mirrors how the FFT simplifies complex calculations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
FFT Efficiency: The FFT algorithm reduces the computation time for DFT from O(NΒ²) to O(N log N).
-
Divide-and-Conquer: The FFT uses this method to break down the DFT calculation into smaller, manageable parts.
-
Applications: FFT is widely used in audio processing, image compression, and communication systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of calculating the FFT for an 8-point DFT shows how it divides the computation into smaller segments, significantly reducing operation count.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
FFT can be so swift, like a neat little gift, turning waves into sights, transforming day and night.
π Fascinating Stories
-
Imagine a wizard who needs to sort magical ingredients quickly. He calls upon the FFT β a powerful spell that divides the ingredients into two groups, analyzes them, and combines their effects, saving time to brew his potions!
π§ Other Memory Gems
-
To remember the steps of FFT: 'Divide, Compute, Combine' (DCC)! First, divide the signal, compute smaller DFTs, then combine results.
π― Super Acronyms
FFT = Fast Fourier Transform; think of it as 'Fast Frequency Transformation' to emphasize speed.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fast Fourier Transform (FFT)
Definition:
An efficient algorithm to compute the Discrete Fourier Transform (DFT) with reduced computational complexity.
-
Term: Discrete Fourier Transform (DFT)
Definition:
A mathematical technique for transforming a discrete signal from the time domain to the frequency domain.
-
Term: DivideandConquer
Definition:
An algorithmic approach that divides a problem into smaller sub-problems, solves them independently, and combines their solutions.
-
Term: CooleyTukey Algorithm
Definition:
The most common algorithm for computing the FFT, especially effective when the number of samples is a power of 2.