Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today, weβre going to discuss the Fast Fourier Transform, or FFT. Can anyone tell me why signal processing is important?
It helps us analyze signals, like sounds or images, in a way that's easier to manage.
Exactly! The FFT allows us to transform a signal from the time domain to the frequency domain efficiently. This is crucial in applications like audio processing and communications.
But why is FFT more efficient than calculating DFT directly?
Great question! The DFT is computationally expensive, requiring O(NΒ²) operations, while the FFT reduces that to O(N log N) by using a divide-and-conquer approach. Remember O for operational complexity!
So, that's why we can analyze large datasets quickly?
Yes! Now, to summarize, the FFT not only speeds up the process but also opens doors for real-time processing of signals. Can anyone provide an example of where this might be useful?
Like in music software where we need to adjust frequencies while playing?
Exactly! Such applications benefit immensely from the efficiency provided by the FFT. Let's recap the significance of FFT and its use in signal processing.
Real-time Applications of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs shift our focus to the applications of FFT. Can anyone name a few areas where FFT is actively used?
I think it's used in audio processing?
Yes, absolutely! Itβs utilized for tasks like equalization and filtering in audio systems. Any other applications come to mind?
How about image processing, like JPEG compression?
Correct! FFT helps manipulate the frequency content of images for compression and enhancement. Remember the acronym AIMS: Audio, Image, Modulation, and Speech.
What about in communication systems?
Excellent point! FFT is critical in modulation and demodulation processes, especially in technologies like Wi-Fi and LTE. Let's review these points. FFT has applications in audio processing, image compression, communication systems, and more.
Key Steps in FFT Computation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's dive into how the FFT actually works. Who can outline the basic process of the FFT algorithm?
It divides the DFT into smaller DFTs.
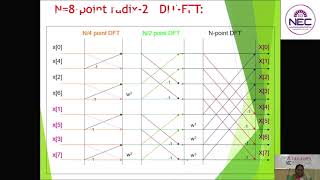
Right! It uses a divide-and-conquer strategy. Initially, it splits the signal into even and odd indexed samples. Why do you think this is effective?
Because it reduces the complexity?
Exactly! By breaking down the problem, we can compute smaller components more easily and combine them at the end. Can someone summarize the key steps?
Divide, compute smaller DFTs, and combine!
Perfect! These steps illustrate why FFT is so efficient. Always remember: Divide, Compute, Combine. Letβs ensure we grasp these fundamentals before we move on.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Fast Fourier Transform (FFT) significantly optimizes the computation of the Discrete Fourier Transform (DFT), reducing the complexity from O(NΒ²) to O(N log N), thus enabling real-time analysis of signals in various fields such as audio processing and communications.
Detailed
Introduction to Fast Fourier Transform
The Fast Fourier Transform (FFT) is an essential algorithm in signal processing that enables the efficient computation of the Discrete Fourier Transform (DFT). The FFT makes it possible to analyze signals in the frequency domain by significantly reducing computational complexity from O(NΒ²) to O(N log N). This efficiency is critical for handling large datasets and real-time applications such as audio processing, image enhancement, and communication systems. In this chapter, we will delve deeper into Fourier Analysis, the foundation of the FFT, examine the inner workings of the FFT algorithm, and explore its applications and implementations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is the Fast Fourier Transform (FFT)?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Fast Fourier Transform (FFT) is one of the most fundamental algorithms in signal processing. It efficiently computes the Discrete Fourier Transform (DFT), which is used to analyze signals in the frequency domain.
Detailed Explanation
The Fast Fourier Transform is a crucial algorithm used in signal processing to analyze frequency components of signals. It allows us to perform the Discrete Fourier Transform, which transforms a signal represented in time into its representation in frequency. This transformation is powerful because it helps us understand what frequencies are present in a signal, which is essential for various applications such as audio signal processing and image analysis.
Examples & Analogies
Think of the FFT as a musical tuner. When you play a note, it not only helps you identify the note you're playing (the time-based representation) but also tells you which frequencies are involved in that note. Just like a tuner can help you analyze a musical sound, the FFT helps analyze signals in various applications.
Importance of FFT in Signal Processing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The FFT dramatically reduces the computational complexity of performing a DFT, making it feasible to analyze large datasets in real-time applications such as audio processing, image processing, and communications.
Detailed Explanation
Calculating the Discrete Fourier Transform directly can take a lot of time, especially with large datasets. The FFT makes this process much faster by reducing the number of calculations needed. This efficiency allows us to apply signal processing techniques in real-time, such as analyzing audio while it is being played or processing video streams instantly.
Examples & Analogies
Imagine trying to find a specific book in a library without an organized system - it would take an immense amount of time. Now, think of the FFT as a cataloging system that quickly decides which section contains the book you need, allowing you to find your book almost instantly. Similarly, FFT helps find frequency components quickly from complex signals.
Overview of the Chapter's Content
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this chapter, we will review the theory behind Fourier Analysis, which is the foundation for understanding the FFT, and explore how the FFT algorithm works, its applications, and its implementation.
Detailed Explanation
This chapter will discuss various topics essential for understanding the FFT, starting with the theoretical foundations of Fourier Analysis. It will cover how the FFT actually functions, where it can be applied, and how one can implement it in practical scenarios. By understanding these elements, readers will gain a well-rounded view of how FFT fits into the broader field of signal processing.
Examples & Analogies
Think of the chapter as a roadmap for a journey into the world of frequency analysis. Just as a roadmap gives you directions and highlights points of interest along the way, this chapter provides the necessary knowledge, leading you through the essentials of FFT, its workings, and how to use it in real-world situations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
FFT: An efficient algorithm to compute DFT, crucial for real-time signal analysis.
-
Applications of FFT: Used in audio, image processing, and communication systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using FFT in audio equalization to adjust specific frequency ranges in real-time music playback.
-
Implementing FFT in image processing for JPEG compression to reduce file size while retaining image quality.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
FFT makes signals fast, for processing, it's unsurpassed!
π Fascinating Stories
-
Imagine a musician who needs to adjust their song instantaneously. The FFT is like their sound technician who can quickly find and enhance every frequency, making the song sound perfect.
π§ Other Memory Gems
-
Remember FFT as 'Fast Findings in Time', highlighting its efficiency.
π― Super Acronyms
FFT = Fast Fourier Transform; think F for Fast, F for Fourier, T for Transform!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fast Fourier Transform (FFT)
Definition:
An algorithm for efficiently computing the Discrete Fourier Transform (DFT).
-
Term: Discrete Fourier Transform (DFT)
Definition:
A transformation used to convert a finite list of equally spaced samples of a function into an equivalent finite list of coefficients of a finite combination of complex exponentials.
-
Term: Signal Processing
Definition:
The analysis, interpretation, and manipulation of signals.