Fast Fourier Transform: Review of Fourier Analysis
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome everyone! Today, we'll dive into Fourier Analysis. Can anyone tell me what Fourier Analysis is?

Is it a method for analyzing signals?

Absolutely! Fourier Analysis allows us to represent a signal as a sum of sinusoidal functions. This is crucial for analyzing the frequencies present in the signal. Let's use the acronym **SINE**: Signals IN New Examinations.

So, it helps in finding out how much of each frequency is in a signal?

Exactly! By breaking signals into components, we can see their frequency content clearly.
Understanding the FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss the Fast Fourier Transform or FFT. Who can explain why we need FFT instead of directly calculating the DFT?

Because calculating DFT directly can be really slow for large datasets?

That's right! The direct computation is O(N²), which is inefficient. The FFT reduces this to O(N log N). Remember, think of it as speeding up the process significantly!

How does it do that?

Great question! It uses a divide-and-conquer approach by breaking down the DFT calculations into smaller parts.
Applications of FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s now talk about some applications of the FFT. Can anyone name one?

Maybe audio processing?

Precisely! FFT is widely used in audio processing for tasks like filtering and equalization. It's like using a **SPEECH** to remember: Signal Processing Efficiently Enhances Audio.

What about in image processing?

Excellent! FFT is used in image compression techniques such as JPEG.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section reviews Fourier Analysis, which allows signals to be represented as sums of sinusoidal functions. It covers the Continuous-Time and Discrete-Time Fourier Transforms, the DFT, and the FFT's significance in reducing computational complexity, making real-time signal analysis possible.
Detailed
Fast Fourier Transform: Review of Fourier Analysis
The Fast Fourier Transform (FFT) is pivotal in modern signal processing, transforming the analysis of signals from the time domain to the frequency domain effectively. By dramatically lowering the computational complexity involved in calculating the Discrete Fourier Transform (DFT), the FFT has made it possible to work with large datasets in applications such as audio and image processing, communications, and more.
Key Concepts:
- Fourier Analysis: A technique for decomposing signals into sinusoidal components, allowing for frequency-based analysis.
- Continuous-Time Fourier Transform (CTFT): Converts continuous-time signals into frequency-domain representations.
- Discrete-Time Fourier Transform (DTFT): Transforms discrete-time signals into their frequency domain.
- Discrete Fourier Transform (DFT): Samples the DTFT, processing a finite number of frequencies.
- Fast Fourier Transform (FFT): An efficient algorithm using a divide-and-conquer strategy to compute the DFT quickly, reducing complexity from O(N²) to O(N log N).
Applications of FFT:
- Analyzing audio signals, image processing, speech recognition, and more, the FFT provides essential tools for understanding signal frequency content efficiently.
The understanding of FFT and Fourier Analysis forms the basis for advancements in the electronic communication age, highlighting its importance in both theoretical and practical realms.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to FFT
Chapter 1 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Fast Fourier Transform (FFT) is one of the most fundamental algorithms in signal processing. It efficiently computes the Discrete Fourier Transform (DFT), which is used to analyze signals in the frequency domain. The FFT dramatically reduces the computational complexity of performing a DFT, making it feasible to analyze large datasets in real-time applications such as audio processing, image processing, and communications. In this chapter, we will review the theory behind Fourier Analysis, which is the foundation for understanding the FFT, and explore how the FFT algorithm works, its applications, and its implementation.
Detailed Explanation
The Fast Fourier Transform (FFT) is crucial in signal processing. It enables us to analyze and interpret signals by transforming them from the time domain to the frequency domain efficiently. Instead of directly calculating the Discrete Fourier Transform (DFT), which involves many computations and can be slow, the FFT provides a faster method to obtain the same frequency information, especially useful in real-time scenarios. This chapter will cover Fourier Analysis, the fundamentals of FFT, its operational mechanisms, applications, and how to implement it effectively.
Examples & Analogies
Think of the FFT like a super-efficient librarian. If you need to find specific articles in a vast library (analogous to a dataset), the librarian can quickly sift through shelves (time domain) to pull out the relevant volumes (frequency domain) for you, rather than having you search through every book (which would be the DFT). This allows you to obtain the information you need much faster.
Fourier Analysis: The Foundation
Chapter 2 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fourier analysis is a method of representing a signal as a sum of sinusoidal functions (complex exponentials), each with its own amplitude, frequency, and phase. This decomposition allows signals, which may be complex or non-periodic, to be analyzed in terms of their frequency content.
Detailed Explanation
Fourier Analysis involves breaking down complex signals into simpler sine and cosine waves, which represent periodic functions. Each sinusoidal component can be described by three parameters: amplitude (how strong the wave is), frequency (how fast it oscillates), and phase (where it starts in its oscillation). By understanding these components, we can analyze the overall signal's frequency content effectively.
Examples & Analogies
Imagine a musical band where each instrument plays a different note. Each note represents a pure sine wave. If you want to understand what music the band is playing (the overall signal), you'd want to know which instruments are playing and how loudly (the amplitude) they're playing (the frequency components). Fourier analysis helps you break down that complex sound into individual notes.
Continuous-Time Fourier Transform (CTFT)
Chapter 3 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Continuous-Time Fourier Transform (CTFT) is used to analyze continuous-time signals in the frequency domain. It transforms a time-domain signal x(t) into its frequency-domain representation X(f). The CTFT is defined as:
X(f)=∫−∞∞x(t)e−j2πft dt
Where:
- X(f) is the frequency-domain representation of x(t).
- j is the imaginary unit.
- f is the frequency variable.
- x(t) is the continuous-time signal.
The CTFT converts a continuous signal into a continuous spectrum that shows how much of each frequency is present in the signal.
Detailed Explanation
The Continuous-Time Fourier Transform (CTFT) enables the transition from analyzing a signal over time to understanding it in terms of its frequency components. The mathematical formula shows how the integral accumulates contributions of all possible frequencies, creating a continuous spectrum that displays the signal's frequency content. The outputs, X(f), indicate the magnitude and phase of the sinusoids that compose the original signal.
Examples & Analogies
Think of a CTFT as a chef who is trying to understand a dish made with a mix of spices (the signal x(t)). By tasting bits of the dish at various moments (analyzing continuously over time), the chef can deduce the mix and proportion of each spice (the frequency components) used in the recipe.
Discrete-Time Fourier Transform (DTFT)
Chapter 4 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For discrete-time signals, the Discrete-Time Fourier Transform (DTFT) is used to convert a signal from the time domain to the frequency domain. The DTFT of a discrete-time signal x[n] is given by:
X(f)=∑n=−∞∞x[n]e−j2πfn
Where:
- X(f) is the frequency-domain representation of x[n].
- x[n] is the discrete-time signal.
- f is the frequency variable (continuous).
The DTFT gives a continuous frequency spectrum for discrete-time signals, similar to the CTFT for continuous signals.
Detailed Explanation
The DTFT applies to discrete signals, converting them into a similar frequency representation as the CTFT for continuous signals. The DTFT formula utilizes a summation instead of an integral, reflecting that the input signal consists of samples taken at discrete intervals. This transformation is fundamental for analyzing digital signals that are commonly used in computers and electronic devices.
Examples & Analogies
If the CTFT is like a chef sampling an entire dish, then the DTFT is like a food critic taking specific bites at set intervals during a meal. Though the critic's experience is discrete, by combining all those bites (samples), they still get a sense of the meal's overall flavors (frequency content).
Discrete Fourier Transform (DFT)
Chapter 5 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Discrete Fourier Transform (DFT) is the sampled version of the DTFT. It is used when the signal is sampled at discrete time intervals and represents the signal as a sum of sinusoidal components, but only for a finite number of frequencies. The DFT is defined as:
X[k]=∑n=0N−1x[n]e−j2πknN for k=0,1,…,N−1
Where:
- X[k] is the frequency-domain representation of x[n].
- x[n] is the discrete-time signal with N samples.
- k is the frequency index.
- N is the number of samples.
The DFT provides a discrete set of frequency components, corresponding to the frequencies k/N for k=0,1,…,N−1. The DFT is periodic with a period of N, meaning that after the N-th frequency, the frequency components repeat.
Detailed Explanation
The Discrete Fourier Transform (DFT) directly relates to how we sample a continuous signal. It takes a finite number of samples from a discrete signal and computes its representation in the frequency domain. This means that after computing the DFT, we only get specific frequencies rather than a continuous range. The periodic nature of the DFT is critical; it shows that some results will repeat, which is important to consider in practical applications.
Examples & Analogies
Imagine a student recording their grades every quarter (samples). When they look at their final year grades (DFT), they only get those recorded scores (finite frequencies) algebraically averaged, but since grades might be repetitive (periodicity), the final score can echo earlier grades, providing a cyclic view of their performance.
Fast Fourier Transform (FFT)
Chapter 6 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Fast Fourier Transform (FFT) is an algorithm designed to efficiently compute the DFT. The direct computation of the DFT from the formula involves O(N2) operations, which becomes computationally expensive for large values of N. The FFT reduces this complexity to O(Nlog N), making it much faster and more suitable for real-time applications.
Detailed Explanation
The FFT is a clever algorithm that improves the DFT's efficiency by reducing the number of computational operations needed. While the DFT requires N^2 operations, the FFT manages to accomplish the same task using only N*log(N) operations. This reduction makes it feasible to handle larger data sets quickly, which is crucial in modern applications where speed is a priority.
Examples & Analogies
Think of the FFT like using a highway to reach a city instead of taking small backroads that crisscross the countryside. The backroads represent the longer, more tedious path (DFT), while the highway allows you to travel quickly and directly to your destination (the desired frequency analysis).
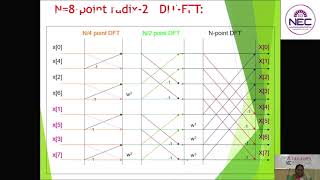
Example of FFT
Chapter 7 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider a simple example of an N=8 point DFT computation. Instead of computing the DFT directly from the definition, the FFT algorithm would divide the 8-point DFT into smaller 4-point DFTs, and each 4-point DFT would be further divided into 2-point DFTs. This recursive process reduces the number of operations significantly.
Detailed Explanation
In this example, we break down a more complex DFT problem into manageable pieces using FFT. The process involves recursively dividing the signal into smaller sections, solving them individually, and then combining these solutions. By exploiting patterns and symmetries within the data, the overall computational effort decreases significantly, showing how efficient the FFT can be.
Examples & Analogies
Imagine a large jigsaw puzzle (the DFT) divided into smaller sections (4-point and 2-point DFTs). Instead of trying to assemble the whole puzzle at once, you work on small sections first. Once each section is complete, you combine them to see the bigger picture (full DFT). This method is faster and less overwhelming.
Applications of FFT
Chapter 8 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The FFT is a powerful tool with many applications in various fields of signal processing. Some common applications include: 1. Signal Analysis: The FFT is widely used to analyze the frequency content of signals, such as audio signals, communications signals, and vibrations in mechanical systems. 2. Audio Processing: FFT is used in real-time audio processing for tasks like equalization, filtering, and spectral analysis. 3. Image Processing: FFT is used in image compression (such as JPEG) and in image enhancement, where the frequency content of an image is manipulated. 4. Speech Recognition: The FFT is employed in speech recognition systems to analyze the frequency spectrum of the human voice. 5. Communication Systems: FFT is fundamental in communication systems for modulation and demodulation, especially in OFDM (Orthogonal Frequency Division Multiplexing) systems like Wi-Fi and LTE. 6. Radar and Sonar: FFT is used in radar and sonar systems to detect and analyze signals reflected from objects, helping in distance and velocity measurement.
Detailed Explanation
The applications of FFT are extensive, spanning various industries due to its efficiency in processing signals. In signal analysis, it helps to dissect the frequency components of different signals to understand their characteristics deeply. In audio processing, for instance, it aids in enhancing sound quality and filtering unwanted noise. In communications, FFT facilitates the transmission and reception of signals in a way that maximizes performance.
Examples & Analogies
Similar to how a chef blends spices to create intricate flavors in a dish, the FFT allows engineers and scientists to blend different types of data to create useful analyses. For example, just as a chef can quickly adjust seasoning to improve a meal, technicians can utilize FFT to quickly adjust signals for better clarity and performance.
Properties of the Fourier Transform and FFT
Chapter 9 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Fourier Transform, and by extension the FFT, has several important properties that make it useful in signal processing: 1. Linearity: The Fourier Transform is linear, meaning that the transform of a weighted sum of signals is the weighted sum of the individual transforms. 2. Time Shifting: Shifting a signal in the time domain corresponds to a phase shift in the frequency domain. Specifically, if x(t) has Fourier transform X(f), then x(t−t0) has Fourier transform X(f)e−j2πft0. 3. Scaling: Scaling a signal in the time domain corresponds to an inverse scaling in the frequency domain. 4. Convolution: Convolution in the time domain corresponds to multiplication in the frequency domain. This is particularly useful for filtering operations, as convolution is the process by which filters are applied to signals. 5. Parseval's Theorem: Parseval's Theorem states that the total energy in a signal is preserved when transforming from the time domain to the frequency domain.
Detailed Explanation
The properties of Fourier Transform and FFT enhance their utility in signal processing. For example, linearity means that combining signals simply combines their transformations, making analysis simpler. Time shifting and scaling allow for seamless adjustments in the frequency representation. Convolution property enables easier filtering by transforming multiplication in the frequency domain to time-domain processes. Lastly, Parseval's Theorem provides a critical connection by showing energy conservation during transformations.
Examples & Analogies
Consider properties of FFT like rules in a board game. Each rule helps you navigate scenarios effectively. For instance, just like knowing that moving a piece forward translates the game position (time shift), understanding the transformations ensures strategies are applied correctly without losing essential information in the analysis.
Example: Applying FFT to a Signal
Chapter 10 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider a signal x(t) that is a sum of two sinusoidal signals: x(t)=sin (2π5t)+sin (2π15t). We can sample this signal at 50 Hz and compute its FFT. The result will show two prominent peaks at 5 Hz and 15 Hz, corresponding to the frequencies of the sinusoidal components. In Python, using the numpy and matplotlib libraries, we can perform the FFT and visualize the frequency content of the signal.
Detailed Explanation
In this example, we study a specific signal composed of two sine waves. By sampling the signal at 50 Hz and applying FFT, we can extract its frequency components. The peaks observed in the FFT results at 5 Hz and 15 Hz indicate the presence of these frequencies in the original signal. The code provided allows for computational verification and visualization using Python, showing how FFT reveals the frequency spectrum effectively.
Examples & Analogies
When you turn up the volume on a stereo while playing music, you hear different notes distinctly. Similarly, when applying FFT to the signal we created, it reveals which notes (frequencies) are present by displaying their strengths on the graph. This allows us to appreciate the 'music' of the signal through its frequency components.
Conclusion
Chapter 11 of 11
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Fast Fourier Transform (FFT) is a key algorithm in signal processing, allowing for efficient computation of the Discrete Fourier Transform (DFT). The FFT provides a fast and computationally efficient way to analyze the frequency content of signals, enabling real-time processing in many applications. Understanding Fourier analysis and the FFT is essential for tasks such as signal analysis, audio processing, image processing, communication systems, and much more. The FFT reduces the complexity of frequency-domain analysis from O(N2) to O(Nlog N), making it feasible to work with large datasets in real-time.
Detailed Explanation
In conclusion, the FFT is a revolutionary algorithm in signal processing, significantly improving the speed and efficiency of frequency analysis. Its utility in numerous applications underlines its importance in modern technology and engineering. By transforming the complexity of frequency-domain calculations from O(N^2) to O(N log N), it opens up new possibilities for real-time data processing across a diverse range of fields.
Examples & Analogies
Much like how a powerful computer can complete tasks in a fraction of the time it would take a manual process, the FFT streamlines signal analysis, empowering engineers and scientists with faster results. In a world driven by data, FFT represents the capability to handle vast information efficiently, akin to having a super-efficient assistant who gets the work done faster than the traditional way.
Key Concepts
-
Fourier Analysis: A technique for decomposing signals into sinusoidal components, allowing for frequency-based analysis.
-
Continuous-Time Fourier Transform (CTFT): Converts continuous-time signals into frequency-domain representations.
-
Discrete-Time Fourier Transform (DTFT): Transforms discrete-time signals into their frequency domain.
-
Discrete Fourier Transform (DFT): Samples the DTFT, processing a finite number of frequencies.
-
Fast Fourier Transform (FFT): An efficient algorithm using a divide-and-conquer strategy to compute the DFT quickly, reducing complexity from O(N²) to O(N log N).
-
Applications of FFT:
-
Analyzing audio signals, image processing, speech recognition, and more, the FFT provides essential tools for understanding signal frequency content efficiently.
-
The understanding of FFT and Fourier Analysis forms the basis for advancements in the electronic communication age, highlighting its importance in both theoretical and practical realms.
Examples & Applications
Using FFT, real-time audio processing can efficiently filter unwanted noise from signals.
In image processing, FFT helps compress images significantly by manipulating their frequency representation.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
FFT, don't fret, it speeds up the vet, for signals we get, just let it be set!
Stories
Imagine a detective breaking down a large case into smaller, manageable ones, just as the FFT breaks down a DFT into smaller DFTs using clues.
Memory Tools
Use the mnemonic SPEECH for remembering FFT applications: Signal Processing Efficiently Enhances Audio, Communications, and Healthcare.
Acronyms
Remember **DANCE**
Divide
Analyze
Combine
with Efficient execution for FFT.
Flash Cards
Glossary
- Fast Fourier Transform (FFT)
An efficient algorithm to compute the Discrete Fourier Transform (DFT) with a complexity of O(N log N).
- Discrete Fourier Transform (DFT)
A finite transformation used when the signal is sampled at discrete intervals.
- ContinuousTime Fourier Transform (CTFT)
Transforms continuous-time signals into their frequency-domain representations.
- DiscreteTime Fourier Transform (DTFT)
A transformation that converts discrete-time signals to their frequency representation.
- Signal Processing
The analysis, interpretation, and manipulation of signals.
Reference links
Supplementary resources to enhance your learning experience.
