Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing the Fast Fourier Transform, or FFT. It's crucial for efficiently computing the Discrete Fourier Transformβhas anyone heard of the DFT before?
I've heard of it! It's used to analyze signals, right?
Exactly! The DFT can be computationally expensive without the FFT, which improves efficiency significantly. Can anyone guess how it reduces the computing time?
Does it break the problem into smaller parts?
Yes! It uses a divide-and-conquer strategy. Remember, FFT = Fast, Fury = Fewer computations!
Understanding the Steps
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's delve into the steps of the FFT algorithm. What happens first?
The signal gets divided into smaller parts, right?
Correct! We take even and odd indexed samples. Can someone explain why this is helpful?
It helps simplify the calculations by reducing the size of the problem!
Exactly! After dividing, we recursively compute the DFT of these smaller parts before combining them. Remember: DSOβDivide, Solve, and Organize!
Cooley-Tukey Radix-2 FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
One of the most common implementations of the FFT is the Cooley-Tukey Radix-2 algorithm. What makes it special?
I think it works best when N is a power of two?
That's right! Thus, it efficiently works with larger datasets by ensuring good performance at these sizes. Does anyone have a mnemonic to remember this?
How about 'Powerful Pairs for Processing?'
Great mnemonic! It reminds us that using powers of two leads to powerful computational efficiencies!
Importance of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, letβs talk about why FFT matters. Can anyone share an application of FFT?
I think it's used in audio signal processing!
Exactly! FFT is vital in real-time applications. It also plays a big role in image processing and communication signals. How about we summarize today with 'Analyze Signals Like a Pro!'?
Thatβs a great way to remember why FFT is essential!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains the Fast Fourier Transform (FFT) algorithm, highlighting its divide-and-conquer approach to computing the Discrete Fourier Transform (DFT) more efficiently. By recursively breaking down the DFT computation, the FFT significantly reduces the number of operations required, allowing for practical analysis of large datasets.
Detailed
Understanding How FFT Works
The Fast Fourier Transform (FFT) serves as an efficient algorithm for computing the Discrete Fourier Transform (DFT), which is essential in signal processing. Without the FFT, directly calculating the DFT would involve a computational cost of O(NΒ²), making it impractical for larger datasets. The FFT reduces this complexity to O(N log N).
Key Features of the FFT Algorithm
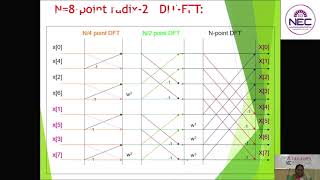
The FFT algorithm is fundamentally based on a divide-and-conquer method. It breaks down the DFT computation into smaller, manageable DFTs, leveraging specific symmetries in the DFT formula. One widespread implementation of this algorithm is the Cooley-Tukey Radix-2 FFT, which is particularly useful when the sample size, N, is a power of two.
Steps of the FFT Algorithm
- Divide the Signal: The first step involves separating the signal into two smaller segments based on the even and odd indexed samples.
- Recursive Computation: The DFT of each smaller segment is computed recursively.
- Combine Results: Finally, the results of the smaller DFTs are combined to form the complete DFT.
By recursively breaking down the computations, the FFT efficiently handles frequency analyses of larger datasets, making it an invaluable tool in real-time signal processing applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The FFT algorithm is based on the divide-and-conquer approach. It recursively divides the DFT computation into smaller DFTs, exploiting symmetries in the DFT formula. The most common implementation of the FFT is the Cooley-Tukey Radix-2 FFT algorithm, which works efficiently when the number of samples N is a power of 2.
Detailed Explanation
The Fast Fourier Transform (FFT) is a method that speeds up the calculation of the Discrete Fourier Transform (DFT). Its foundation lies in the divide-and-conquer strategy, which means it breaks down a complex problem into simpler parts. Specifically, the FFT algorithm takes a signal and divides it into smaller pieces that can be managed more easily. This division continues until the simplest possible computations of DFT are reached. The Cooley-Tukey Radix-2 FFT is the most commonly used method because it works best when the number of data points, N, is a power of two, such as 2, 4, 8, 16, etc. This structure helps streamline the calculations through symmetry.
Examples & Analogies
Imagine you are trying to cut a pizza into equal slices for a party. If you have a standard round pizza, you could cut it into 8 equal slices if you have 8 guests. Now, to serve the pizza quickly, instead of cutting directly, you decide to cut the pizza in half first, making two large halves, and then cut each half into 4 slices. This method of dividing the task of slicing the pizza into smaller, manageable steps is similar to how FFT divides the DFT calculation.
Key Steps of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The key steps of the FFT algorithm are:
1. Divide the signal into two smaller signals (even and odd indexed samples).
2. Recursively compute the DFT of each smaller signal.
3. Combine the results to form the full DFT.
Detailed Explanation
The FFT process involves three main steps. First, the algorithm takes a signal and splits it into two smaller sequences: one containing samples at even indices and another containing samples at odd indices. This division helps in simplifying the complexity of the original DFT computation. Next, the FFT algorithm computes the DFT of these smaller signals. Since these smaller DFTs are easier to calculate, the algorithm uses the same divide-and-conquer strategy recursively until even the smaller signals reach a manageable size. Finally, the results of these smaller DFT computations are combined. This combination reconstructs the full DFT more efficiently than if it were computed directly from the original signal.
Examples & Analogies
Think of this process like a group project in school. Suppose your teacher asks your class to write a report. Instead of everyone working on different sections and facing confusion, the teacher splits the class into small groups. Each group focuses on a specific part of the report. Once each group has completed its section, they come back together to combine their parts into one cohesive report. In the same way, FFT breaks the signal into manageable parts to solve the problem more efficiently.
Efficiency of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By recursively breaking down the DFT into smaller DFTs, the FFT achieves a computational complexity of O(N log N), making it suitable for large datasets.
Detailed Explanation
The efficiency of the FFT is primarily due to its nature of breaking the problem down recursively. In mathematical terms, using the FFT allows us to compute the DFT in O(N log N) operations, which is significantly faster than the traditional approach that takes O(N^2) operations. This reduced computational complexity is crucial, especially when dealing with large datasets, such as in audio analysis or image processing, where time and resources are often limited. Thus, the FFT makes it practical to perform real-time signal processing.
Examples & Analogies
Consider a library filled with thousands of books. If someone were to organize the books one by one by comparing their titles, it would take a long time. However, if the librarian were to divide the books into smaller sections based on categoriesβlike fiction, non-fiction, and referenceβthey could organize each section individually and then combine the collections. This way, organizing the books becomes much faster, just as the FFT makes it faster to compute frequency data from large signals.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
FFT Algorithm: An efficient method for computing the DFT by recursive division.
-
Divide-and-Conquer Strategy: A methodology that simplifies complex problems by breaking them down into smaller parts.
-
Power of Two: The FFT performs optimally when the dataset size is a power of two.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The FFT makes it possible to analyze a signal of size N=1024 with a complexity of O(1024 log 1024) instead of O(1024Β²).
-
In practical applications, FFT enables real-time audio processing, allowing for tools like equalizers or sound analyzers.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When signals split into even and odd, FFT makes math less hard!
π Fascinating Stories
-
Once in Signal Land, FFT, the magic algorithm, used its powers of divide and conquer to quickly analyze audio data, making the noisy world clearer.
π§ Other Memory Gems
-
DSO - Divide, Solve, Organize, steps in FFT to remember how to compute DFT efficiently.
π― Super Acronyms
FFT - Fast Frequency Transformation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fast Fourier Transform (FFT)
Definition:
An algorithm to compute the Discrete Fourier Transform efficiently using a divide-and-conquer approach.
-
Term: Discrete Fourier Transform (DFT)
Definition:
A mathematical transformation that converts a discrete signal to its frequency components.
-
Term: CooleyTukey Algorithm
Definition:
A common implementation of the FFT that works best when the number of samples is a power of two.
-
Term: Divide and Conquer
Definition:
A problem-solving strategy that breaks a problem down into smaller, more manageable problems.