Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Convolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will discuss convolution, a fundamental operation in signal processing. Can anyone tell me what they think convolution means?
I think itβs about combining two signals somehow.
Exactly! More formally, convolution combines two signals in such a way that we can analyze their combined effect. Itβs a mathematical operation that helps us in many applications. Let's break it down further. When we convolve two signals in the time domain, what do you think happens in the Z-domain?
Isn't it multiplication?
Correct! The Z-Transform of the convolution of two signals is the product of their Z-Transforms. This is a crucial concept for analyzing systems. Remember: Convolution in time domain = multiplication in Z-domain! To help remember that, we can use the acronym **C-M** - Convolution-Multiplication.
Mathematical Definition of Convolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs look at the mathematical definition. For two discrete-time signals x[n] and h[n], convolution is defined as $$ (x * h)[n] = \sum_{k=-\infty}^\infty x[k] \cdot h[n-k] $$ . Can anyone explain what this equation means?
You're summing up the product of one signal shifted by n and the other signal.
Exactly, Student_3! This summation effectively blends two signals together, where each value of n represents a unique point in time. By shifting h[n] and multiplying by x[k], we incorporate the impact of h[n] on each sample of x[n].
So, if we know h[n] (the impulse response), we can derive the output signal?
Precisely! Thatβs the power of convolution in linear systems. Just remember, for simplification, we can always use that the Z-Transform turns convolution into multiplication.
Applications of Convolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, letβs discuss some applications. How do you think convolution is used in digital signal processing?
In filtering signals?
Exactly right! We often use convolution to design filters. The filter's impulse response h[n] is convolved with the input signal x[n] to get the output. What else do you think?
Image processing might use this too, right?
Absolutely! Convolution plays a significant role in applications like blurring and edge detection in images as well. Itβs the foundation for many signal processing tasks. Who can summarize what we learned about convolution today?
Convolution is combining two signals and it relates to multiplication in the Z-domain, and itβs used for filtering and image processing!
Excellent summary! Remember these applications as they will come up often in digital signal processing.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the importance of convolution in understanding the relationship between two discrete-time signals and their Z-Transforms. It highlights that the convolution of two signals results in the multiplication of their corresponding Z-Transforms, an essential concept for analyzing linear systems' outputs.
Detailed
Convolution
In the context of the Z-Transform, convolution is a fundamental operation that correlates two discrete-time signals, allowing for the analysis of their combined effects in a system. Specifically, if we have two signals denoted by x[n] and h[n] with corresponding Z-Transforms X(z) and H(z), the convolution operation in the time domain is expressed mathematically as:
$$(x * h)[n] = \sum_{k=-\infty}^\infty x[k] \, h[n - k]$$
The Z-Transform of the convolution of these two signals is defined by the property:
$$Z\{(x * h)[n]\} = X(z) \cdot H(z)$$
This property is crucial because it simplifies the analysis of linear systems. When the input x[n] and the system's impulse response h[n] are known, we can easily determine the output of the system by simply performing multiplication in the Z-domain. This relationship is crucial for designing digital filters and understanding how systems react to various inputs.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Convolution in Z-Domain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Convolution in the time domain corresponds to multiplication in the Z-domain. If x[n] and h[n] are two discrete-time signals with Z-Transforms X(z) and H(z), respectively, the Z-Transform of their convolution is:
\[(x * h)[n] \xrightarrow{Z} X(z) \cdot H(z)\]
Detailed Explanation
Convolution is a mathematical operation that combines two signals to produce a third. The key point here is that if you take the convolution of two discrete-time signals (like sequences of numbers), the result can be represented in the Z-domain simply by multiplying their individual Z-Transforms. For example, if you have a signal representing a series of data points (x[n]) and another representing the system's response (h[n]), when you convolve them, their combined effect in the Z-domain is just the multiplication of their Z-Transforms (X(z) and H(z)). This property simplifies the analysis of linear systems tremendously.
Examples & Analogies
Think of a restaurant where the x[n] signal represents the orders received throughout the day, and the h[n] signal represents the time it takes to prepare each order. The overall output of meals served during different times of the day can be seen as the convolution of these two signals. In the Z-domain, analyzing this output becomes straightforward because you simply multiply the 'prep time transform' (H(z)) with the 'order pattern transform' (X(z)) to predict how many meals are served over time.
Importance of Convolution Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This property is crucial for analyzing the output of a linear system when the input and impulse response are known.
Detailed Explanation
Understanding the convolution property is vital for system analysis because it allows engineers to determine how different inputs affect the output of a system. In other words, if you know how a system reacts to a certain input (its impulse response), and you have a specific input signal, you can compute the output signal directly using convolution. This is especially useful in engineering and signal processing because it enables quick calculations and predictions without needing to simulate the entire system.
Examples & Analogies
Imagine you're designing a water sprinkler system (the linear system). The impulse response is how the sprinkler distributes water when it is turned on for a short burst. If you know the pattern of the rainfall or water demand (the input), you can convolve that with how your sprinkler works to predict the total water coverage in your garden. This way, you can strategize your watering needs based on expected input patterns.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Convolution: Mathematical operation combining two signals.
-
Z-Transform: Transforms discrete-time signals into the frequency domain.
-
Linear Systems: Systems that can be analyzed using superposition and convolution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
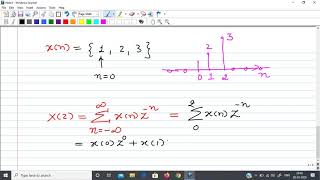
If x[n] = [1, 2, 3] and h[n] = [1, 1], then (x * h)[n] = [1, 3, 5, 3].
-
In image processing, convolution with a filter can enhance edges or blur images.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
For signals that blend, Count all the ways, Convolution's the friend, In time it stays.
π Fascinating Stories
-
Imagine mixing two paint colors. Each stroke combines to create a new hue, just like how convolution mixes signals to generate the output of a system.
π§ Other Memory Gems
-
The mnemonic FAME can help: Find the overlap, Add products, Multiply in Z-domain, Enumerate as a signal.
π― Super Acronyms
The acronym **C*M** stands for Convolution-Multiplication, a quick reminder of the relationship.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Convolution
Definition:
A mathematical operation that combines two discrete-time signals to produce a third signal, representing the amount of overlap of one signal as it shifts over another.
-
Term: ZTransform
Definition:
A mathematical transformation that converts a discrete-time signal into a complex frequency domain to facilitate the analysis of linear systems.