Time and Frequency Domains: Z-Transform
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Z-Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss the Z-Transform, a core concept in discrete-time signal processing. Can anyone tell me what a transform generally does?

It changes a signal from one form to another, like the Fourier Transform changes time signals into frequency signals.

Exactly! The Z-Transform extends that idea to discrete signals, allowing us to analyze both time and frequency characteristics effectively. Can anyone think of why analyzing these characteristics is important?

It helps us understand the behavior of systems based on their stability.

Right! Analyzing stability is crucial, especially for systems that might have complex dynamics.
Mathematical Formulation of the Z-Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into the mathematical definition of the Z-Transform. It’s given by the equation X(z) = ∑(n=-∞ to ∞) x[n] z^{-n}. Who can break this down for us?

The equation says that we sum the products of the discrete signal x[n] with z raised to the power of negative n over all n.

Exactly! And what is the significance of z being a complex variable?

It allows us to analyze the frequency response of the signal at different magnitudes and phases.

Well done! This complexity helps in detailed analysis tailored to system behavior.
Region of Convergence (ROC)
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the Region of Convergence, or ROC. Why do you think the ROC is crucial in using the Z-Transform?

It defines limits where the transformation converges, helping us decide how we can use it for different signals.

Correct! For example, a causal signal has its ROC as a circle in the complex plane centered at the origin. What does that imply in terms of system stability?

If the ROC includes the unit circle, the system is stable!

Exactly! Understanding ROC leads us to crucial insights into the behavior of systems.
Properties of the Z-Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s go over the properties of the Z-Transform. Can anyone name one?

Linearity, meaning the Z-transform of a sum of signals is the sum of their individual transforms.

Very good! Now, can anyone provide another property and its utility?

Time Shifting! It helps analyze delayed signals by shifting the Z-Transform by k samples.

Exactly! These properties enable the analysis of complex systems more simply. Let’s remember them with the acronym LIST—Linearity, Initial/Final Value Theorems, Scaling, and Time Shifting!
Inverse Z-Transform and Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s talk about how we can go back from Z-domain to time domain. What's a common method for the Inverse Z-Transform?

Partial Fraction Expansion is one.

Exactly! This method helps simplify the Z-Transform for easier conversion back to the original signal. Now, can anyone think of applications for the Z-Transform?

Digital filter design and stability analysis in control systems!

Perfect! It plays a critical role in signal processing applications like speech and image analysis as well.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces the Z-Transform, highlighting its definition, properties, and applications in analyzing discrete-time systems. It discusses concepts like the Region of Convergence (ROC) and provides insights into stability analysis, allowing for an effective understanding of system dynamics through the Z-Transform.
Detailed
Detailed Summary of Z-Transform
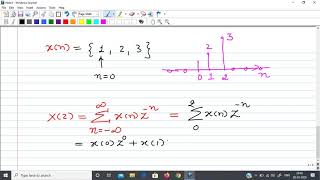
The Z-Transform is essential for converting discrete-time signals into the complex frequency domain, allowing engineers to analyze system behavior effectively. It is mathematically defined as :
X(z) = ∑(n=-∞ to ∞) x[n] z^{-n}.
Where:
- x[n] is the discrete-time signal and X(z) is its Z-Transform. The variable z is complex and represented as z = re^{jω}. The concept's significance extends to the
Region of Convergence (ROC), which informs about signal stability and causality. The Z-Transform possesses critical properties, including linearity, time-shifting, scaling, convolution, and the initial and final value theorems, which aid in discrete signal analysis and system design. Stability in systems is evaluated using the ROC: a system is stable if its ROC includes the unit circle. The Inverse Z-Transform methods are also highlighted, returning the signal from the Z-domain back to the time domain, while applications in control systems and signal processing are discussed.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Z-Transform
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform is a fundamental concept in discrete-time signal processing that generalizes the Fourier Transform to handle discrete signals more effectively, especially for stability analysis and system design. The Z-Transform provides a powerful tool for analyzing the time and frequency-domain characteristics of discrete-time signals and systems, particularly for systems that may not be periodic or that involve complex dynamics.
Detailed Explanation
The Z-Transform is essential in digital signal processing, allowing us to manage discrete signals like digital audio or video more efficiently. It extends the idea of the Fourier Transform, which deals mainly with continuous signals, to discrete signals—those samples taken at specific intervals. This is important for engineering and computer science when working with systems that have irregular behaviors or need to be analyzed in terms of how they respond over time and in various frequency ranges.
Examples & Analogies
Think of the Z-Transform like a camera that captures snapshots of a moving scene (the discrete signals). Each photo represents a moment in time, and the Z-Transform helps us analyze how the entire scene changes—similar to how you might study a movie by looking at each frame individually.
Mathematical Definition of the Z-Transform
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform is the discrete-time counterpart of the Laplace Transform, providing a way to represent discrete signals in the complex frequency domain. It is defined as:
X(z) = ∑n=−∞∞x[n]z−n
Where:
● x[n] is the discrete-time signal.
● X(z) is the Z-Transform of the signal.
● z is a complex variable: z = re^{jω}, where r is the magnitude and ω is the phase angle.
Detailed Explanation
The Z-Transform mathematically represents a sequence of discrete values (like audio samples) in terms of a complex variable z, defined in terms of its magnitude (r) and phase (ω). The formula given allows us to generate a function X(z) that contains all the information about the original signal x[n]. This transformation is crucial because it allows engineers to analyze and manipulate signals within the frequency domain, making it easier to design filters or systems that react predictably.
Examples & Analogies
Imagine you’re trying to analyze a song's various notes played over time. The Z-Transform is like a music sheet where each note (sample) is replaced with musical symbols (the complex function X(z)). This notation allows for easier manipulation, just like musicians can easily adjust the tempo or key of a song using a well-written score.
Region of Convergence (ROC)
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Region of Convergence (ROC) is a crucial concept when working with the Z-Transform. It specifies the values of z for which the Z-Transform converges. The ROC depends on the nature of the signal x[n] and provides insight into the stability and causality of the system.
Key Concepts:
● For Right-Sided Signals: If the signal x[n] is causal (i.e., defined for n ≥ 0), the ROC is typically a circle in the complex plane centered at the origin, with a radius determined by the growth rate of x[n].
● For Left-Sided Signals: If x[n] is anti-causal (i.e., defined for n ≤ 0), the ROC extends from the origin outward, again determined by the decay rate of x[n].
● For Two-Sided Signals: If x[n] is defined for all n, the ROC typically lies between two concentric circles in the complex plane.
The ROC is important for determining the stability and behavior of the system:
● If the ROC includes the unit circle (|z| = 1), the system is stable.
● If the ROC does not include the unit circle, the system is unstable.
Detailed Explanation
The Region of Convergence helps us understand which inputs will lead to a well-defined output when applying the Z-Transform to signal x[n]. The characteristics of the signal determine whether the Z-Transform converges properly. This is essential because it affects how we interpret the stability of the system: a system is stable if the ROC includes the unit circle, meaning that the system behaves predictably over time without producing divergent outputs for a bounded input.
Examples & Analogies
Consider a water fountain. The Region of Convergence is like the area around the fountain where the water sprays consistently and predictably (the stable ROC). If you stand too far away, the water won't reach you (in the unstable region), or if you come too close to the appliance (like a clogged drain), it could cause chaos instead of the serene display you expect (system instability).
Properties of the Z-Transform
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform has several useful properties that make it a powerful tool for analyzing discrete-time signals and systems.
4.4.1 Linearity
The Z-Transform is linear, meaning that if x1[n] and x2[n] are signals with Z-Transforms X1(z) and X2(z), respectively, then:
a x1[n] + b x2[n] → Z a X1(z) + b X2(z)
Where a and b are constants.
4.4.2 Time Shifting
If x[n] has the Z-Transform X(z), then shifting the signal by k samples (i.e., x[n−k]) results in:
x[n−k] → Z z−k X(z)
This property is useful for analyzing systems with delayed responses.
4.4.3 Scaling in the Z-Domain
If x[n] has the Z-Transform X(z), then scaling the signal by a constant a^n (i.e., a^n x[n]) results in:
a^n x[n] → Z X(a z)
This property is particularly helpful when analyzing exponential signals and their impact on the system.
4.4.4 Convolution
Convolution in the time domain corresponds to multiplication in the Z-domain. If x[n] and h[n] are two discrete-time signals with Z-Transforms X(z) and H(z), respectively, the Z-Transform of their convolution is:
(x∗h)[n] → Z X(z) ⋅ H(z)
This property is crucial for analyzing the output of a linear system when the input and impulse response are known.
4.4.5 Initial and Final Value Theorems
The Z-Transform has the following important theorems:
● Initial Value Theorem:
lim n→0 x[n] = lim z→∞ X(z)
● Final Value Theorem:
lim n→∞ x[n] = lim z→1 (z−1) X(z)
These theorems provide a way to find the initial and final values of a discrete-time signal directly from its Z-Transform, without needing to compute the inverse Z-Transform.
Detailed Explanation
The Z-Transform's properties serve as essential tools for making analyses easier. The linearity property allows us to combine signals, while time-shifting and scaling make it straightforward to address signals altered in time or spaced out in magnitude. Convolution being represented as multiplication simplifies complex analyses involving inputs and outputs of discrete systems. The initial and final value theorems help to determine the starting and ending states of signals directly from their Z-Transform, greatly simplifying calculations.
Examples & Analogies
Think about baking a cake. The linearity property is like mixing flour and sugar; you can combine them in various measures without losing their basic qualities. Time-shifting is akin to deciding to bake it for a little longer or taking it out earlier. Scaling is like adjusting the ingredients to make a bigger or smaller cake. Convolution is like combining different layers of flavors, while the initial and final value theorems allow you to predict how the cake will taste when it just comes out of the oven and after it has cooled.
Z-Transform and Stability
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Stability is a critical property of discrete-time systems, and the Z-Transform provides an effective means of analyzing system stability. A system is considered stable if its impulse response h[n] is absolutely summable, meaning that the region of convergence (ROC) for its Z-Transform includes the unit circle (i.e., |z| = 1).
● Causal System Stability: For a causal system, stability is guaranteed if the ROC of the system's Z-Transform includes the unit circle.
● Anti-Causal System Stability: For an anti-causal system, stability requires that the ROC extend from the origin outward and include |z| = 1.
● Two-Sided System Stability: For a two-sided system, the ROC must contain the unit circle for the system to be stable.
A system with a pole inside the unit circle is stable, while a system with a pole outside the unit circle is unstable.
Detailed Explanation
Stability in discrete-time systems is paramount. The characteristic that determines stability is if the impulse response, which describes how a system reacts to external inputs, is absolutely summable. When the ROC includes the unit circle, it's an indicator of predictable system behavior. Stability criteria differ based on system types (causal, anti-causal, or two-sided), emphasizing the importance of the ROC in delivering effective system analysis.
Examples & Analogies
Consider a seesaw—if the weight is balanced correctly (impulse response is summable), it won’t tip over. If too much weight is on one side (ROC not including the unit circle), it’ll flip uncontrollably, leading to instability. Just like the seesaw in different positions represents causal and anti-causal systems, the overall balance reflects the importance of stability in physical structures.
Inverse Z-Transform
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Inverse Z-Transform is used to convert a signal from the Z-domain back to the time domain. Several methods can be used to compute the inverse Z-Transform:
1. Partial Fraction Expansion: This is one of the most commonly used methods, where the Z-Transform is decomposed into simpler fractions, each of which has an easily identifiable inverse.
2. Contour Integration: A more advanced method involving complex integration around a contour in the Z-plane, used for finding the inverse of more complex Z-Transforms.
3. Power Series Expansion: For simple rational functions, a power series expansion can be used to obtain the inverse Z-Transform.
The inverse Z-Transform helps in determining the time-domain response of a system given its Z-domain representation.
Detailed Explanation
The Inverse Z-Transform is essential for translating the results back into a practical time-domain signal. Different methods can be utilized depending on the complexity of the Z-Transform being dealt with. Partial fraction expansion simplifies the problem; contour integration allows for handling complex scenarios, and power series expansion simplifies certain cases—the choice of method often depends on the specific context or signal characteristics.
Examples & Analogies
Think about solving a puzzle. The Z-Transform provides the final picture (the Z-domain), and the inverse Z-Transform is how you piece together the puzzle back into a coherent image (the time-domain signal). Just as different strategies can help piece together puzzles—breaking them down into smaller sections, using the edge pieces first, or looking at patterns—different methods of inverse Z-Transform cater to varying levels of complexity.
Applications of the Z-Transform
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Discrete-Time System Analysis:
- The Z-Transform is widely used to analyze and design digital filters, where it helps in understanding the system's behavior and stability.
- Control Systems:
- In control theory, the Z-Transform is used to analyze discrete-time systems, design controllers, and study system stability.
- Signal Processing:
- The Z-Transform is crucial for processing discrete-time signals in applications like speech processing, image processing, and communication systems.
- Stability and Pole-Zero Analysis:
- The Z-Transform provides a framework for analyzing the poles and zeros of a system, which determine its stability and frequency response.
Detailed Explanation
The Z-Transform plays a significant role across various domains. In discrete-time system analysis, it simplifies filter design, ensuring that systems behave as expected. Control systems rely on it to achieve desired responses and maintain stability. In the realm of signal processing (particularly in digital forms of communication), it's essential for effective handling of sounds, images, and transmissions. Finally, understanding the poles and zeros aids engineers in characterizing system behavior and designing for optimal performance.
Examples & Analogies
Imagine a conductor leading an orchestra. The Z-Transform helps the conductor ensure all instruments play in harmony (digital filters), directs musicians to adjust their timing and pitch (control systems), and balances sounds in concerts (signal processing). The poles and zeros are like the musicians understanding their roles, helping the entire orchestra create beautiful music together by defining their dynamics.
Key Concepts
-
Z-Transform: A mathematical tool for transforming discrete-time signals to the complex frequency domain.
-
Region of Convergence: The area in the Z-plane where the Z-Transform converges, crucial for stability analysis.
-
Causal vs. Anti-Causal Signals: Differently defined signals impacting the nature of ROC.
-
Stability: Dependence on whether the ROC includes the unit circle or not.
Examples & Applications
Example of a causal signal is the unit step function, which starts from zero and moves forward in time.
In a digital filter design, understanding the poles and zeros mapped via the Z-Transform allows for better system stability.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Z's are the keys in the signal domain, helping analyze without any pain.
Stories
Imagine a time traveler (the Z-Transform) who helps discrete signals find their place in the frequency domain, ensuring stability.
Memory Tools
Remember LIST for Z-properties: Linearity, Initial/Final Value, Scaling, Time Shift.
Acronyms
ROC - Regional Occurrence of Convergence.
Flash Cards
Glossary
- ZTransform
A mathematical transform relating a discrete-time signal to its representation in the complex frequency domain.
- Region of Convergence (ROC)
The range of values of z for which the Z-Transform converges.
- Causal Signal
A signal where the values are defined for n ≥ 0.
- AntiCausal Signal
A signal that is defined for n ≤ 0.
- Stable System
A system whose impulse response is absolutely summable.
- Inverse ZTransform
A process to convert a signal from the Z-domain back to the time domain.
Reference links
Supplementary resources to enhance your learning experience.
