Linearity
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Linearity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss the linearity property of the Z-Transform. This property states that the Z-Transform of a sum of signals is equal to the sum of their individual Z-Transforms.

Can you give us an example of this property?

Certainly! If you have two signals, \(x_1[n]\) and \(x_2[n]\), with their respective Z-Transforms of \(X_1(z)\) and \(X_2(z)\), then for any constants \(a\) and \(b\), we can say that: \(a \cdot x_1[n] + b \cdot x_2[n] \xrightarrow{Z} a \cdot X_1(z) + b \cdot X_2(z)\). Does that clarify things?

Yes, but why is this property important?

Great question! It simplifies the analysis of signals in systems, allowing us to break down complex systems into simpler parts we can easily manage.
Applications of Linearity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's now explore the applications of linearity in real-world systems. For instance, when designing filters, we can easily superimpose the effects of multiple signals.

Can you explain how that works in practice?

Certainly! If you know the response of each individual signal, the response of their linear combination can be calculated without needing to analyze the total input signal all at once. That's the power of linearity!

Are there any exceptions to this property?

In the context of the Z-Transform, linearity holds true for linear time-invariant systems, but not for nonlinear systems. That's an important distinction to keep in mind.
Understanding Constants in Linearity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about the constants \(a\) and \(b\) in the linearity property. What do they represent?

Are they just any numbers, or do they have specific meanings?

They can be any real numbers and represent weights for signals. They allow the signal contributions to be adjusted before applying the Z-Transform. For example, if one signal is more significant, you might increase its corresponding constant.

What if one of the constants is zero?

Good observation! If either constant is zero, that signal effectively doesn’t contribute to the sum during the transformation.
Recap and Reinforcement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s summarize what we've learned. The linearity property allows for simplification of signal processing because we can apply the Z-Transform to each component individually and reassemble them later.

So, basically, we can analyze systems much easier if they are linear?

Exactly! Linear systems can often be analyzed using simpler techniques than nonlinear ones, which require much more complex treatment.

What’s the takeaway for using this property?

Always look for opportunities to break down complex signals into simpler, linear combinations! It makes analysis and system design much more efficient.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Linearity is a fundamental property of the Z-Transform, which implies that for any discrete signals, their Z-Transforms can be combined using constants. Understanding this property is essential for analyzing complex systems efficiently.
Detailed
Linearity in Z-Transform
The linearity property of the Z-Transform is crucial for simplifying the analysis of discrete-time signals and systems. Specifically, if we have two discrete signals, \(x_1[n]\) and \(x_2[n]\), with Z-Transforms \(X_1(z)\) and \(X_2(z)\) respectively, then the Z-Transform of a linear combination of these signals is given by:
\[ a \cdot x_1[n] + b \cdot x_2[n] \xrightarrow{Z} a \cdot X_1(z) + b \cdot X_2(z) \]
Where \(a\) and \(b\) are constants. This theorem establishes that the Z-Transform behaves predictively with respect to linear combinations of signals, making it a powerful tool for signal processing and system analysis. The property allows for easier manipulations in both theoretical analysis and practical applications, particularly when dealing with systems where multiple signals may be present.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Linearity in Z-Transform
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform is linear, meaning that if x1[n] and x2[n] are signals with Z-Transforms X1(z) and X2(z), respectively, then:
ax1[n]+bx2[n]→ZaX1(z)+bX2(z)
a x_1[n] + b x_2[n]
ightarrow Z o a X_1(z) + b X_2(z)
Where a and b are constants.
Detailed Explanation
Linearity in the context of the Z-Transform means that the transformation of a linear combination of signals is equivalent to the linear combination of their individual transformations. Specifically, if you have two discrete signals x1[n] and x2[n] with their respective Z-Transforms X1(z) and X2(z), applying a linear combination of these signals—like multiplying x1[n] by a constant 'a' and x2[n] by another constant 'b'—and then taking the Z-Transform results in the same expression as taking the Z-Transforms separately and combining them. This property is crucial for simplifying calculations and understanding how systems respond to combined inputs.
Examples & Analogies
Consider the concept of adding ingredients to a recipe. Suppose you have a recipe that calls for two ingredients: flour and sugar. If you want to make the recipe sweeter, you can add 'a' cups of flour and 'b' cups of sugar to a bowl. When you combine them, the outcome (the batter) is proportional to the amount of each ingredient you added. Similarly, in signal processing, combining two signals in a linear manner results in an output that is also a linear combination of the individual signal outputs, making it easier to analyze complex systems.
Key Concepts
-
Linearity: The concept that allows signals to be superimposed and analyzed individually.
-
Z-Transform: A transformation involving complex variables to analyze discrete-time signals.
Examples & Applications
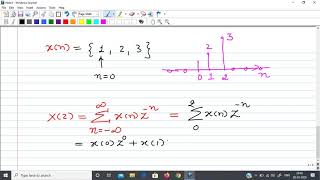
If \(x_1[n] = \{1, 2, 3\}\) has a Z-Transform \(X_1(z)\) and \(x_2[n] = \{4, 5, 6\}\) has \(X_2(z)\), then for constants \(a=2\) and \(b=3\), the Z-Transform of \(2x_1[n] + 3x_2[n]\) can be computed as \(2X_1(z) + 3X_2(z)\).
In a digital filter design, we can apply the linearity property to understand how different frequency responses combine without needing to analyze the overall response directly.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
If two signals you combine, their Z's will align!
Stories
Imagine two friends bringing distinct ingredients to a party. When they each contribute their flavors, the combined taste becomes irresistible, just as two signals create a unique output when transformed together.
Memory Tools
Remember 'Z for a Sum' to recall that additions in the Z-domain can be handled like sums in regular algebra.
Acronyms
L.S.A. = Linearity Simplifies Analysis. Keep this in mind when dealing with complex signals.
Flash Cards
Glossary
- ZTransform
A mathematical transformation that converts discrete-time signals into a complex frequency domain representation.
- Linearity
A property that states the output of a linear system is a linear combination of its inputs.
- Discretetime signal
A signal that is defined only at discrete points in time, generally represented as x[n].
Reference links
Supplementary resources to enhance your learning experience.
