Introduction
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Basics of Z-Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will explore the Z-Transform, which is critical in analyzing discrete-time signals. It's essential for stability analysis and system design.

Why do we need the Z-Transform instead of just using the Fourier Transform?

Great question! The Z-Transform is more effective for discrete signals, especially when those signals may have complex dynamics or aren't periodic. It helps us analyze the behavior of systems in both time and frequency domains.

Can you explain what you mean by complex dynamics?

Sure! Complex dynamics refer to systems that exhibit behaviors like stability, instability, or varying response based on different inputs. The Z-Transform allows us to capture these variations efficiently.

So, is the Z-Transform similar to something like the Laplace Transform?

Absolutely! The Z-Transform is the discrete-time equivalent of the Laplace Transform and is essential in system analysis.

What are some examples of systems where we use the Z-Transform?

Examples include digital filters, control systems, and any situation where we need to analyze discrete-time signals.

In summary, the Z-Transform provides powerful tools for analyzing signals that can't be captured well with traditional methods. We will delve deeper into its properties in our next sessions.
The Importance of Stability in Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Stability is crucial in system design. Let's discuss how the Z-Transform assists in determining the stability of a discrete-time system.

How does the Z-Transform help us understand stability?

The Z-Transform allows us to see where the Z-transform converges. If the area where it converges includes the unit circle, the system is stable. If not, it’s unstable.

What happens if a system is unstable?

An unstable system may lead to unpredictable output and could fail in real-world applications. That's why assessing stability using the Z-Transform is essential.

Can you give an example of stability affecting a system?

Certainly! In digital control systems, instability can result in oscillations, making it challenging to control temperature in heating systems.

So stability is not just a theoretical concept?

Exactly! It has practical implications. Understanding stability helps us design more effective systems. Let’s summarize: the Z-Transform aids in assessing system stability and ensuring reliable performance.
Applications of Z-Transform in Signal Processing
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's look at some practical applications of the Z-Transform. It is prevalent in digital signal processing.

What kind of applications are we talking about?

The Z-Transform is used in analyzing and designing digital filters, which are essential for audio and video processing.

Can it be used in communication systems too?

Absolutely! It’s crucial in optimizing signal transmission and minimizing errors during data transfer.

What about control systems? Are they also reliant on the Z-Transform?

Yes! The Z-Transform helps design controllers that can handle discrete-time signals effectively in automation processes.

So, it's clear the Z-Transform plays a vital role in many signal processing applications.

Exactly! Understanding its applications helps us see its relevance in real-world systems. To summarize: the Z-Transform is applicable in digital filters, control systems, and communication, making it essential for signal processing.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces the Z-Transform, emphasizing its role in discrete-time signal processing. It extends the Fourier Transform for analyzing non-periodic signals and is essential for understanding system stability and behavior.
Detailed
Detailed Summary
The Z-Transform is a crucial tool in the field of discrete-time signal processing that enhances the analysis of discrete signals, particularly in terms of system stability and design. Unlike the Fourier Transform, which is primarily suited for continuous and periodic signals, the Z-Transform generalizes these concepts to handle discrete signals that exhibit complex dynamics and behaviors. In this section, the foundation of the Z-Transform is laid, highlighting its importance in analyzing discrete-time systems and outlining its unique properties. As we explore further in this chapter, the Z-Transform will facilitate detailed examination of systems, emphasizing stability and dynamic behavior in both time and frequency domains.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
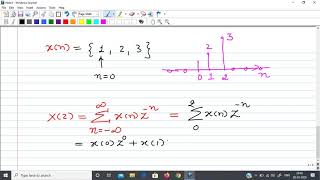
What is Z-Transform?
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform is a fundamental concept in discrete-time signal processing that generalizes the Fourier Transform to handle discrete signals more effectively, especially for stability analysis and system design.
Detailed Explanation
The Z-Transform is a mathematical tool used in signal processing that allows us to analyze discrete-time signals. Unlike the Fourier Transform, which is suitable for continuous signals, the Z-Transform extends this concept to discrete sequences, making it particularly useful for determining the stability of systems and for designing systems that handle discrete data effectively.
Examples & Analogies
Think of the Z-Transform like a magnifying glass for signal analysis. Just as a magnifying glass helps you see fine details in a picture that are otherwise hard to notice, the Z-Transform enables engineers to analyze the properties of signals that may exhibit complex behaviors, which are critical in fields like telecommunications and audio processing.
Purpose of the Z-Transform
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Z-Transform provides a powerful tool for analyzing the time and frequency-domain characteristics of discrete-time signals and systems, particularly for systems that may not be periodic or that involve complex dynamics.
Detailed Explanation
The main purpose of the Z-Transform is to help engineers and scientists understand how signals behave over time and how they can be transformed into the frequency domain. This is especially important for systems that do not repeat in a regular fashion (non-periodic) or that have intricate behaviors that traditional analysis methods might not handle well. By applying the Z-Transform, one can gain insights into both the immediate (time-domain) and broader (frequency-domain) behaviors of these systems.
Examples & Analogies
Imagine you're trying to analyze music. The time-domain view shows you how sound changes in intensity over time (the waveform), while the frequency-domain view shows you which notes (frequencies) are present in the music. The Z-Transform helps you switch between these views efficiently, just like a musical score allows musicians to see the structure of the piece while rehearsing its rhythm.
Chapter Overview
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In this chapter, we will introduce the Z-Transform, its properties, and its relationship with the time and frequency domains. We will also explore how the Z-Transform is used to analyze discrete-time systems, especially in the context of stability and system behavior.
Detailed Explanation
This section outlines what the chapter will cover regarding the Z-Transform. It indicates that students will learn not only about the Z-Transform itself but also its key properties and how it relates to the two domains of time and frequency. Additionally, we will discuss how the Z-Transform plays a crucial role in analyzing systems that operate on discrete signals, particularly focusing on their stability and overall behavior.
Examples & Analogies
Consider a roadmap for a journey. This overview serves as the roadmap for our exploration of the Z-Transform in this chapter. Just as the roadmap outlines the main stops and the routes we'll take, this section gives a clear structure of the topics we’ll cover: starting from understanding the Z-Transform itself, moving on to its features, and finally applying it to real systems.
Key Concepts
-
Z-Transform: A tool for analyzing discrete-time signals in system design and stability.
-
Stability: A crucial aspect ensuring systems produce predictable responses.
-
Causality: Systems with outputs dependent only on current and past inputs.
Examples & Applications
In digital audio processing, the Z-Transform is utilized to create filters that enhance sound quality.
In automatic control systems, the Z-Transform helps predict how the system will respond to various inputs over time.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Z-Transform's the way to go, for signals that don’t flow.
Stories
Imagine a clever engineer who uses the Z-Transform for various systems, exploring how they behave in time and stability, like a detective solving a mystery.
Memory Tools
Remember Z as 'Zooming in on signals' and Transform as 'Changing from time to frequency'.
Acronyms
Z in Z-Transform stands for 'Zone' of analysis in the discrete 'Transform' of signals.
Flash Cards
Glossary
- ZTransform
A mathematical transform that converts discrete-time signals into the complex frequency domain for analysis.
- DiscreteTime Signal
A signal defined at discrete times, often represented in sequences.
- Stability
The property of a system to produce bounded outputs for bounded inputs over time.
- Complex Domain
A mathematical space where signals are represented in terms of complex numbers.
- Causality
A property of a system where the output depends only on present and past inputs, not future ones.
Reference links
Supplementary resources to enhance your learning experience.
