Damped vs Undamped Free Vibration (Introduction to Damping)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damping
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the concept of damping in vibrational systems. Can anyone tell me what an undamped system is?

Isn't it a system where the oscillations go on forever with the same amplitude?

Exactly! In undamped systems, oscillations continue indefinitely. Now, how do real structures compare?

They would have some kind of energy loss, right?

Correct! Real structures experience energy dissipation due to internal friction, air resistance, and more. This is a crucial reason why we need to understand damping.

Can you explain what changes in the equation with damping included?

Of course! The new equation includes a damping coefficient, which alters how the system behaves. This leads us to explore essential damping characteristics next.
Damping Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's look at the modified equation of motion for a damped system: $mx¨(t) + cx˙(t) + kx(t) = 0$. What do the variables represent?

Does ‘m’ represent mass, ‘k’ represents stiffness, and ‘c’ represents the damping coefficient?

Precisely! And what do you think happens when we introduce the damping coefficient?

It changes the system's response based on how damped or undamped it is?

Right again! The behavior is then described by the damping ratio: $ζ = \frac{c}{2√{km}}$. This ratio is crucial for understanding whether a system is critically damped, underdamped, or overdamped.

So, the damping ratio helps determine how the oscillations behave?

Exactly! The damping ratio plays a key role in applications like earthquake-resistant design.
Practical Implications of Damping
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s connect the dots: how does understanding damping affect real-world structures, specifically during seismic events?

It helps engineers create structures that can handle vibrations better, right?

Absolutely! By using this knowledge, engineers can design buildings that avoid resonance with earthquake frequencies.

And they use tools to measure damping, like the logarithmic decrement, correct?

Yes, exactly! This practical measure helps them understand how fast oscillations decay in real structures. It's all about ensuring safety!

I see, so damping is not just theory; it has real implications in engineering.

Well put! Damping directly impacts how we ensure the safety and integrity of structures in seismic zones.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section outlines the differences between damped and undamped free vibrations. It emphasizes the importance of understanding damping for real-world applications, particularly in structural dynamics. The introduction of the damping coefficient leads to modifications in the differential equation, ultimately affecting system behavior through the damping ratio.
Detailed
Damped vs Undamped Free Vibration (Introduction to Damping)
This section serves as a pivotal transition from the examination of undamped free vibration systems to a more complex, realistic understanding that incorporates damping. In undamped systems, oscillations continue indefinitely with a consistent amplitude; however, real structures inevitably experience energy dissipation due to various factors, including internal material friction, air resistance, and slippage at connections.
Key Modifications in the Equation of Motion:
When dampers are introduced, the original equation of motion for an undamped Single Degree of Freedom (SDOF) system:
$$mx¨(t) + kx(t) = 0$$
is modified to include a damping term, yielding:
$$mx¨(t) + cx˙(t) + kx(t) = 0$$
Here, c represents the damping coefficient. The behavior of such a system becomes dependent on the damping ratio, defined as:
$$ζ = \frac{c}{2\sqrt{km}}$$
This change lays the foundational understanding necessary to tackle critical, underdamped, and overdamped systems, especially in the context of designing earthquake-resistant structures.
Consequently, this section highlights the significant impact damping has on system behavior and sets the groundwork for future chapters that will delve deeper into vibration analysis.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Damping in Vibrations
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Although this chapter primarily focuses on undamped systems, a brief understanding of damping is essential for transitioning to real-world systems.
Detailed Explanation
This section starts by acknowledging that most of the chapter has been about undamped systems, which theoretically oscillate forever at a constant amplitude. Damping is introduced as a necessary concept for understanding how actual structures behave because all real systems experience some form of energy loss. Without accounting for damping, our analysis would not accurately reflect what happens in the real world during vibrations.
Examples & Analogies
Imagine a swing that keeps moving back and forth without ever slowing down — that's like an undamped system. Now, think of a swing at a park that gradually comes to a stop after being pushed. The slowing down represents the effects of damping, caused by air resistance and friction.
Energy Dissipation in Real Structures
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Real structures exhibit energy dissipation due to internal material friction, air resistance, and connection slippage.
Detailed Explanation
In this chunk, we learn that real-world structures do not just vibrate endlessly. They lose energy over time due to various factors. Internal friction occurs within materials when they are deformed. This friction converts kinetic energy into heat, causing the oscillations to decay. Air resistance similarly works against the motion, and slippage at connections can also absorb energy. Therefore, understanding these dissipation mechanisms is crucial for engineers who design structures that will experience vibrations.
Examples & Analogies
Think of a car driving on a bumpy road. As the tires hit bumps, energy is absorbed by the suspension system, and you feel the car slow down. This energy absorption is similar to what happens in structures during vibrations, where the energy gets dissipated instead of allowing continued oscillation.
Modification of the Equation of Motion
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Introduction of damping modifies the differential equation: mx¨(t)+cx˙(t)+kx(t)=0 where c = damping coefficient.
Detailed Explanation
The mathematical representation of motion changes when damping is included. The equation now incorporates a term (cx˙(t)) that represents the damping force. 'c' is the damping coefficient, which quantifies how much resistance the system faces when it vibrates. By including this term, engineers can more accurately model the behavior of real systems and predict how they will respond to dynamic forces.
Examples & Analogies
Consider a car's brakes. When you apply them, they exert a force that slows down the car. This braking force can be thought of as analogous to the damping force in the vibration equation — both act against motion to reduce speed and eventually bring it to rest.
Damping Ratio and Its Importance
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
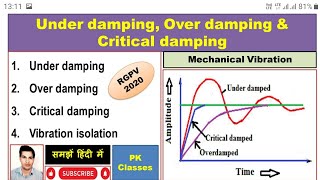
The behavior of the system then depends on the damping ratio: ζ = c / (2√km).
Detailed Explanation
The damping ratio (ζ) provides insight into how a system behaves under vibration. It is calculated based on the damping coefficient (c), mass (m), and stiffness (k) of the system. The value of ζ can classify systems as underdamped, critically damped, or overdamped, which affects how quickly they return to equilibrium after being disturbed. Understanding this ratio helps engineers design structures that can withstand forces, such as those from earthquakes, without experiencing damaging vibrations.
Examples & Analogies
Imagine a swinging pendulum. If it just stops (overdamped), continues to swing for a long time (underdamped), or comes to rest exactly at the equilibrium point without overshooting (critically damped), each scenario presents a different damping ratio. Knowing which type of damping applies helps engineers design more effective structures.
Key Concepts
-
Damping: The energy dissipation in vibrational systems.
-
Damping Coefficient (c): A term in the equation that quantifies damping.
-
Damping Ratio (ζ): A dimensionless measure of damping effect.
-
Damped vs Undamped: The distinction between real-life energy losses and ideal systems.
Examples & Applications
A bridge experiencing wind-induced vibrations will have damping effects due to friction and material properties.
A guitar string produces damped vibrations, leading to a gradual decrease in sound amplitude over time.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Damping is the stage where energy doth fade, in real-world motion, it helps keep us safe.
Stories
Imagine a dancer on stage, swirling in vivid spins. As they dance longer, their momentum fades; this represents how damping reduces motion in vibrational systems over time.
Memory Tools
Remember 'Dampened Down' for the effects damping has on system behavior.
Acronyms
DAMP - Damping Affects Motion Parameters, a quick reminder of how damping influences a system.
Flash Cards
Glossary
- Damping
The process through which energy is dissipated in a vibrating system, resulting in a decrease in amplitude over time.
- Damping Coefficient (c)
A parameter that quantifies the amount of damping in a system, influencing its response to vibrations.
- Damping Ratio (ζ)
A dimensionless measure that describes the degree of damping in a system relative to critical damping.
- Undamped System
A vibrational system that oscillates indefinitely without any decrease in amplitude.
Reference links
Supplementary resources to enhance your learning experience.
