Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Natural Frequency
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we’re going to talk about natural frequency in a Single Degree of Freedom system. Can anyone tell me what they think natural frequency is?
Is it the speed at which the system vibrates?
Exactly! The natural frequency, denoted by ωₙ, tells us how fast the system oscillates when it’s disturbed. It’s calculated by the formula ωₙ = √(k/m). Does anyone remember what k and m represent?
k is the stiffness of the spring and m is the mass!
Correct! So, we see that increasing the stiffness will increase the natural frequency. Here's a simple mnemonic: 'Stiffer springs sing faster' to help remember that stiffer springs lead to higher frequencies. Any questions about that?
How does changing mass affect the natural frequency?
Good question! Increasing mass actually decreases the natural frequency. So if we think of our earlier mnemonic, we could say 'More mass sings slower.' Let's review: What does ωₙ depend on?
It depends on both mass and stiffness!
Well done! That's key to understanding free vibrations in structures.
Defining Time Period
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s discuss the time period. Who can tell me what the time period signifies in an oscillating system?
Is it the time for one complete cycle of oscillation?
Exactly! The time period (T) is expressed with the formula T = 2π√(m/k). So, who can link the time period with natural frequency for us?
If the time period increases, then the natural frequency decreases, right?
Spot on! They are inversely related. Let's remember: 'As time stretches, frequency forgets'. Was that clear to everyone?
Yes, that helps a lot! Can we see how this looks in an equation?
Sure! Given T and ωₙ, T can also be written as T = 2π/ωₙ. So the relationship is clear. Let's summarize: What affects the time period, and how does it link to natural frequency?
It’s influenced by mass and stiffness, and they’re inversely related through the formulas!
Great job, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Natural frequency and time period are critical parameters of SDOF systems that determine how quickly a system oscillates when undergoing free vibration. These parameters depend on the mass and stiffness of the system, where natural frequency is calculated as sqrt(k/m) and the time period as 2π√(m/k).
Detailed
Natural Frequency and Time Period
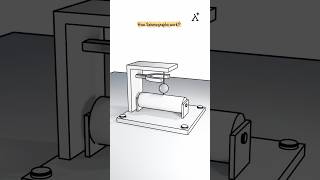
In the study of vibrations, particularly in mechanical systems like the Single Degree of Freedom (SDOF) system, two important intrinsic properties emerge: Natural Frequency (ₙ) and Time Period (T).
Natural Frequency (ₙ)
The natural frequency indicates how rapidly a system oscillates, expressed in radians per second:
oωₙ = √(k/m)
Where:
- k is the stiffness of the spring,
- m is the mass of the system.
Time Period (T)
The time period signifies the time taken for one complete cycle of oscillation:
oT = 2π√(m/k)
Both the natural frequency and time period are crucial for understanding the dynamic behavior of structures subjected to vibrations, especially in seismic activities, as they dictate the oscillation characteristics of the system under free vibration.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Natural Frequency (ωₙ)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Natural Frequency (ωₙ):
ωₙ = √(k/m) (in radians/sec)
Detailed Explanation
Natural frequency, denoted as ωₙ, is a crucial parameter that indicates how fast a system oscillates when it vibrates freely. It depends on two factors: the stiffness of the spring (k) and the mass of the system (m). The formula ωₙ = √(k/m) tells us that if the stiffness increases, the natural frequency increases, making the system oscillate faster. Conversely, if the mass increases while stiffness remains constant, the natural frequency decreases, causing slower oscillations.
Examples & Analogies
Think of a swing in a playground. If you push the swing harder (increasing stiffness), it goes back and forth faster (higher natural frequency). But if you put a heavy child on the swing (increasing mass), it swings more slowly (lower natural frequency). Thus, the relationship between mass, stiffness, and natural frequency can be easily observed in such everyday scenarios.
Time Period (T)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Time Period (T):
T = 2π√(m/k) (in seconds)
Detailed Explanation
The time period, represented by T, is the time taken for one complete cycle of oscillation. The formula T = 2π√(m/k) connects the time period with mass and stiffness. A larger mass or a smaller stiffness results in a longer time period, meaning it takes more time to complete one oscillation. Conversely, a smaller mass or a stiffer spring will reduce the time period, allowing the system to complete its oscillations more quickly.
Examples & Analogies
Imagine a pendulum clock. If we add weight to the pendulum (increase mass), it swings more slowly, resulting in a longer tick-tock sound (longer time period). If we make the pendulum shorter (increase stiffness), it swings back and forth quicker, leading to a shorter tick-tock sound (shorter time period). This analogy helps relate the concepts of time period to tangible experiences in daily life.
Intrinsic Properties of the System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The natural frequency and time period are intrinsic properties of the system and determine how fast or slow the system oscillates under free vibration.
Detailed Explanation
Natural frequency and time period are fundamental characteristics of any oscillating system. These properties remain constant for a given mass and stiffness, meaning they reflect how the system will behave without external forces applied. This knowledge is essential for predicting how structures will respond to dynamic loads, such as during an earthquake or other vibrations.
Examples & Analogies
Consider a guitar string. The tension (stiffness) and mass of the string determine the pitch of the note it produces (natural frequency). When you pluck the string, it vibrates at a frequency that corresponds to its intrinsic properties. Understanding these properties helps guitar makers design strings that produce specific tones, much like engineers design structures to withstand dynamic forces based on their natural frequencies.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Natural Frequency: The oscillation speed of an SDOF system determined by its mass and stiffness.
-
Time Period: The time taken for one complete cycle of oscillation in an SDOF system.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a spring with stiffness k = 400 N/m and mass m = 4 kg is considered, the natural frequency is calculated as ωₙ = √(400/4) = 10 rad/s, resulting in a time period T = 2π√(4/400) = 0.628 s.
-
For a system with a soft spring (k = 100 N/m) and a heavy mass (m = 10 kg), ωₙ would be lower, showing a longer time period for oscillation than in a stiffer, lighter system.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Spring won’t sing fast, when mass holds it back, light springs go like a flash!
📖 Fascinating Stories
-
Imagine a heavy chef trying to flip a pancake - with more mass, it takes longer to spin, just like our time period in a heavier system.
🧠 Other Memory Gems
-
Remember: 'Less Mass, More Time; Stiff Springs, Fast Vibes!'
🎯 Super Acronyms
N.F. for Natural Frequency, where 'N' keeps it natural and 'F' drives the force!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Natural Frequency (ωₙ)
Definition:
The rate at which a system oscillates in the absence of external forces, calculated as ωₙ = √(k/m).
-
Term: Time Period (T)
Definition:
The duration of one complete cycle of oscillation, given by the formula T = 2π√(m/k).
-
Term: Mass (m)
Definition:
The quantity of matter in a body, which influences the natural frequency in vibration systems.
-
Term: Stiffness (k)
Definition:
A measure of a spring's resistance to deformation, affecting the natural frequency of oscillation.