Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the equation of motion for a Single Degree of Freedom system. Can anyone remind me what this equation looks like?
Is it mx¨(t) + kx(t) = 0?
Exactly! Now, when we divide through by the mass m, what do we get?
We get x¨(t) + ω²x(t) = 0, where ω is the natural circular frequency!
Great! That's the foundation. This equation tells us about free vibrations without any damping or external forces.
So, how do we find solutions to this equation?
Good question! The general solution involves trigonometric functions. Let's explore that.
General Solution Overview
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The general solution can be expressed as x(t) = A cos(ω_n t) + B sin(ω_n t). Why do you think we use both sine and cosine?
Because they represent different aspects of oscillation?
Yes, they give us complete information about the motion!
Exactly! A and B are constants determined by initial conditions. If we know the initial displacement and velocity, we can find A and B.
Can you give an example of how these constants are determined?
Certainly! If the initial displacement x(0) = x₀ and initial velocity x˙(0) = v₀, we can use those to find A and B.
Harmonic Form
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Besides the general solution, we can also represent it in a harmonic form: x(t) = X cos(ω_n t + ϕ). What does this form reveal?
It shows the amplitude and phase, which can be really useful!
Absolutely! So the amplitude X relates to the maximum displacement while the phase angle ϕ indicates the timing of the oscillation.
How do we connect this back to A and B?
Great connection! We can find X and ϕ using relationships like X = √(A² + B²). Remember these relationships; they are super handy.
Summary and Application
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To summarize, we examined the general solution of the equation of motion for undamped SDOF systems. Why is this important in real-world applications?
It helps us predict how buildings react to forces like earthquakes!
And understanding the initial conditions is crucial in designing structures!
Exactly, excellent points! Mastering these concepts provides a foundational understanding vital for further studies in structural dynamics and earthquake engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
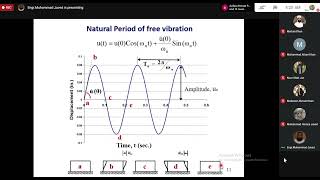
In this section, we examine the general solution to the equation of motion for an undamped SDOF system, detailing how the solution incorporates initial conditions through constants A and B, leading to two equivalent forms: trigonometric and harmonic. The relationship to amplitude and phase angles is also introduced.
Detailed
Solution to the Equation of Motion
In this section, we focus on the mathematical solution to the equation of motion for an undamped Single Degree of Freedom (SDOF) system undergoing free vibrations. This system’s motion can be described using a second-order linear differential equation.
General Solution
The general solution to the equation of motion is expressed as:
$$x(t) = A ext{cos}(\omega_n t) + B ext{sin}(\omega_n t)$$
Where:
- x(t) represents the displacement of the system as a function of time.
- A and B are constants that depend on the initial conditions of the system.
- \omega_n is the natural circular frequency defined as \omega_n = \sqrt{\frac{k}{m}}, where k is the spring constant and m is the mass.
Alternative Harmonic Form
Alternatively, the solution can also be represented in harmonic form as:
$$x(t) = X\text{cos} (\omega_n t + \varphi)$$
Where:
- X is the amplitude of vibration, which provides an intuitive understanding of the range of motion.
- \varphi is the phase angle, representing the initial conditions.
The parameters A and B can be related to initial displacement and velocity as:
$$X = \sqrt{A^2 + B^2}, \; \tan(\varphi) = \frac{B}{A}$$
This structure of the solution highlights how the system responds when set into motion, laying the groundwork for further analysis in vibrations and seismic design.
Youtube Videos
![Numerical from past question on basic structural dynamics||Earthquake Engineering|| [Lec-2]](https://img.youtube.com/vi/36ApBVBLxhA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Solution Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution to the second-order differential equation is of the form:
x(t)=Acos(ωₙ t)+Bsin(ωₙ t)
Detailed Explanation
The equation presented is a general solution to the equation of motion for an undamped Single Degree of Freedom (SDOF) system. Here, x(t) represents the displacement at any time t, A and B are constants that will affect the shape of the motion, and ωₙ is the natural frequency of the system. Essentially, the displacement can be described using a combination of cosine and sine functions, which means that the motion will be periodic or oscillatory.
Examples & Analogies
Think of a child on a swing. When the swing is set into motion, it moves back and forth in a periodic way. The height of the swing at any given moment can be represented by a cosine or sine function, where the maximum height corresponds to A (the amplitude) and the movement back and forth can be represented by these trigonometric functions.
Constants Determined by Initial Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
- A and B are constants determined by initial conditions (initial displacement x₀ and initial velocity ẋ₀).
Detailed Explanation
The constants A and B in the solution are not arbitrary; they are determined by the initial conditions of the system. For example, if we know how far the system is displaced from its equilibrium position (initial displacement, x₀) and how fast it was moving at that moment (initial velocity, ẋ₀), we can calculate the specific values for A and B. This personalizes the equation to reflect the actual conditions of the system at t=0.
Examples & Analogies
Imagine stretching a rubber band and then letting it go. The initial stretch (displacement) and how fast you let it go (velocity) determine how the rubber band will move afterward. In the same way, the values of A and B define the specific motion of the system based on its start.
Harmonic Form of the Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Alternatively, using the harmonic form:
x(t)=Xcos(ωₙ t+ϕ)
Detailed Explanation
Another way to express the displacement is in the harmonic form, where X is the amplitude of vibration, and ϕ is the phase angle. The phase angle is crucial because it indicates the position of the wave relative to time, showing how the wave starts at an offset rather than just beginning at zero displacement. This form emphasizes the oscillatory nature of the motion, encompassing both amplitude and phase shifts.
Examples & Analogies
Consider a wave traveling through the ocean. The height of the wave is like the amplitude X, and the phase angle ϕ determines where the wave starts when we begin to observe it. This is akin to tuning into a specific point in the wave's cycle rather than starting when it is at rest.
Relating Constants to Initial Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These parameters can be related back to the initial conditions using:
B
X=√A² +B²,
tan(ϕ)=
A
Detailed Explanation
The relationships presented here allow us to connect the constants A and B with the initial conditions of the system. Specifically, we can find the amplitude X as a function of A and B, showing that the total energy of oscillation is related to the quadratic sum of A and B. Furthermore, the tangent of the phase angle (ϕ) is expressed through the ratio of these constants, providing a mathematical means to derive critical parameters of the system's motion from its initial state.
Examples & Analogies
Picture a triangle: if you know two sides, you can find the hypotenuse. Similarly, knowing the coefficients A and B helps you find the amplitude and phase, shaping your understanding of the system's behavior starting from its initial conditions. This is like knowing a car’s speed and direction to figure out where it will be later.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Equation of Motion: Governs the dynamic response of an SDOF system.
-
Natural Frequency: Denoted by ω_n, defines the system's vibrational frequency.
-
General Solution: The expression x(t) = A cos(ω_n t) + B sin(ω_n t) represents the system's motion.
-
Initial Conditions: Initial displacement x₀ and initial velocity v₀ are necessary for determining constants A and B.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If an SDOF system is released from an initial displacement of 0.1m and has a velocity of 0m/s, the constants A and B can be determined based on this setup.
-
In engineering, knowing the amplitude and phase angle helps in designing structures to dampen vibrations effectively.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In SDOF systems where the spring is tight, / Natural frequency rules the oscillation's flight.
📖 Fascinating Stories
-
Imagine a child on a swing, drawing back and forth. The constants A and B dictate how far and how fast they swing, just like our system's motion is determined by initial conditions.
🧠 Other Memory Gems
-
For Free Vibrations, remember ‘A’ is for Amplitude while ‘B’ is for Beginning motion.
🎯 Super Acronyms
ACCORD
- Amplitude
- Constants
- Oscillation
- Relationships
- Determine the motion!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Equation of Motion
Definition:
A mathematical relationship that describes the motion of an object based on forces acting upon it.
-
Term: Single Degree of Freedom (SDOF)
Definition:
A system that can move oscillating in only one direction or mode.
-
Term: Natural Frequency (ω_n)
Definition:
The frequency at which a system naturally vibrates when not subjected to external forces.
-
Term: Amplitude (X)
Definition:
The maximum displacement from the equilibrium position in an oscillating system.
-
Term: Phase Angle (ϕ)
Definition:
A measure of the timing of the oscillation relative to the starting point.
-
Term: Initial Conditions
Definition:
The values of displacement and velocity at time t=0, used to determine constants in the motion equation.