Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Free Vibration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into free vibration in a Single Degree of Freedom system. Can anyone tell me what free vibration means?
Isn't it when something vibrates on its own after being disturbed?
Exactly! It's the natural oscillation of a system without external forces acting on it. Remember, 'free' means no outside influences, just the mechanical properties at work.
So, what's a good example of that?
Think of a swing at a park; if you push it and let go, it swings back and forth naturally. Great job! Now, moving on to what defines an SDOF system...
Characteristics of SDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
An SDOF system is typically represented by a mass and a spring. Why do you think this model is used?
Because it simplifies the analysis?
Exactly! This simplicity allows us to understand complex behaviors by breaking them down. In our model, there's only one mass, one direction of motion, and we neglect damping at this stage.
What's damping again?
Great question! Damping refers to energy loss in systems due to factors like friction. We’ll explore that later.
Free Vibration: Equations and Solutions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The equation of motion for an undamped SDOF system is mx¨(t) + kx(t) = 0. Who can explain what each variable represents?
m is mass, and k is stiffness, right?
Correct! And what follows from this equation?
The solution involves cos and sin functions.
Exactly! We use x(t) = Acos(ωₙt) + Bsin(ωₙt) to describe motion, with A and B as constants influenced by initial conditions. Remember, this shows how systems oscillate.
Understanding Natural Frequency
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s talk about natural frequency ωₙ. Can anyone tell me how it's calculated?
It's the square root of stiffness over mass?
That's right! And what does this natural frequency indicate about the system?
How fast it will oscillate?
Precisely! So a stiffer system vibrates faster, while a heavier system vibrates slower.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section examines the dynamics of free vibration in SDOF systems, discussing definitions, equations of motion, and the importance of parameters like natural frequency and time period. It emphasizes the significance in structural dynamics and earthquake engineering.
Detailed
Detailed Summary
Free Vibration Introduction
The free vibration of a Single Degree of Freedom (SDOF) system is an essential topic in structural dynamics. This section highlights that free vibration occurs when a mechanical system vibrates naturally without external forces after an initial disturbance.
Definition and Idealization of SDOF
An SDOF system can be defined as a system characterized by a mass that moves in only one direction, connected to a spring with a defined stiffness. In undamped systems, the motion is governed purely by the mass-spring dynamic, represented simply by displacement over time.
Equation of Motion and Solution
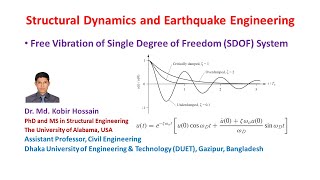
The general equation of motion for an undamped SDOF system is given by mx¨(t) + kx(t) = 0, indicating the relationship between mass (m), spring stiffness (k), and displacement (x). The resulting solution illustrates periodic motion described by cosine and sine functions, with amplitude and phase determined by initial conditions.
Natural Frequency and Time Period
The section defines the natural frequency (ωₙ, derived from the square root of the stiffness divided by the mass) and the time period (T), which are fundamental characteristics of any vibratory system.
Energy and Motion Representation
Total mechanical energy in free vibration remains constant, with oscillations transitioning between kinetic and potential forms. Graphical representations of the system's motion reinforce the concept of continuous energy exchange in an ideal undamped scenario.
Practical Implications
This foundational understanding lays the groundwork for further topics like resonance, damping characteristics, and their implications for real-world structural engineering applications, especially in earthquake zones.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Free Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The study of vibrations is a foundational concept in structural dynamics and earthquake engineering. A structure, when subjected to dynamic forces such as those generated by earthquakes, responds with motion that can be understood and predicted through vibration theory. One of the most basic and important systems in vibration analysis is the Single Degree of Freedom (SDOF) system. The understanding of free vibration of an SDOF system, in the absence of any external forces and damping, lays the groundwork for more complex dynamic analysis and is essential in seismic design and assessment of structures.
Detailed Explanation
In engineering, particularly in understanding structures during earthquakes, vibrations play a crucial role. When buildings or structures experience forces from earthquakes, they move in specific ways, and we can predict these movements using vibration theory. The Single Degree of Freedom (SDOF) system is one of the simplest forms of these vibrations and serves as a fundamental building block for analyzing more complicated systems. Understanding how an SDOF system vibrates without any outside influences gives engineers the essential knowledge they need for designing buildings that are safe during seismic events.
Examples & Analogies
Think of a swing at a playground. When you push it (the initial disturbance) and let go, it swings back and forth due to gravity and its own momentum. The swing's motion is a simple version of how structures might vibrate when subjected to forces like earthquakes.
Definition of Free Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Free vibration refers to the motion of a mechanical system when it is allowed to vibrate naturally without the influence of external forces after an initial disturbance. For a SDOF system, this typically involves a mass-spring system set into motion and allowed to oscillate freely.
Detailed Explanation
Free vibration occurs when a system, once disturbed, moves on its own without any external forces acting on it. A classic example of this is a mass attached to a spring. When you pull the mass down and let go, it will move up and down in a predictable manner due to the spring's characteristics. This is important in engineering as it helps predict the behavior of structures under natural conditions following disturbances like earthquakes.
Examples & Analogies
Imagine a car on a smooth road that suddenly hits a bump (the initial disturbance). After the bump, the car will bounce on its suspension system without any additional pushes from the driver; this bounce is akin to free vibration.
Idealization of SDOF System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A single degree of freedom system is characterized by:
- One mass (m) which can move in only one direction.
- One spring with stiffness (k).
- No damping or external forcing (for the undamped case).
- A displacement function x(t) which fully describes the motion.
This system is often represented by a mass attached to a spring that can move vertically or horizontally, depending on the setup.
Detailed Explanation
An SDOF system simplifies the analysis of vibrational motion. It consists of just one mass that can only move in one direction (either vertically or horizontally) and is connected to a spring that returns it to its equilibrium position. In theories of vibration, considering this simplified model allows engineers to focus on fundamental behaviors without complicating factors like damping or multiple dimensions. The equation of motion for such a system describes how the mass will change its position over time based on forces exerted by the spring.
Examples & Analogies
Think of a single pendulum – like a swing – that can move back and forth. This pendulum represents an SDOF system where the swing is the mass, and the chains are the spring keeping the swing in motion, moving in just one direction: back and forth.
Equation of Motion for Free Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The general equation of motion for an undamped SDOF system undergoing free vibration is:
mx¨(t)+kx(t)=0
Where:
- m = mass of the system
- k = stiffness of the spring
- x(t) = displacement as a function of time
- x¨(t) = acceleration (second derivative of displacement)
Dividing the equation by m, we get:
x¨(t)+ω2x(t)=0
Where ω = √(k/m) is the natural circular frequency of the system.
Detailed Explanation
The equation of motion describes how the mass in an SDOF system behaves over time when it vibrates freely. The left side represents the forces acting on the mass due to its acceleration and the spring, while the right side equals zero, indicating no external forces are involved. By dividing this equation by the mass (m), you arrive at a form that relates the mass, spring stiffness, and acceleration to a characteristic frequency of the system, which is essential for understanding vibration behavior.
Examples & Analogies
Imagine a rubber band: when you pull it and then let it go, it snaps back. The rubber band (spring) tries to pull the mass (your hand) back to its original position, and this behavior can be described mathematically using the equation of motion.
Solution to the Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution to the second-order differential equation is of the form:
x(t) = Acos(ωₙ t) + Bsin(ωₙ t)
Where:
- A and B are constants determined by initial conditions (initial displacement x₀ and initial velocity ẋ₀).
Alternatively, using the harmonic form:
x(t) = Xcos(ωₙ t + ϕ)
Where:
- X = amplitude of vibration
- ϕ = phase angle
These parameters can be related back to the initial conditions using:
B/X = √(A² + B²), tan(ϕ) = A/B.
Detailed Explanation
When solving the equation of motion, we find a general solution that describes the displacement of the mass over time. The solution is sinusoidal, meaning it uses sine and cosine functions, which occur frequently in nature, particularly for oscillations. The constants A and B depend on the starting conditions of the system, such as how far the mass was displaced originally and its speed. This mathematical representation helps predict the specific motion of the mass at any time t.
Examples & Analogies
Think of water waves at the beach: they rise and fall rhythmically. The mathematical functions (sine and cosine) describe the height of the water over time, similar to how the displacement of the mass in the SDOF system changes over time.
Natural Frequency and Time Period
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Natural Frequency (ωₙ):
ωₙ = √(k/m) (in radians/sec)
Time Period (T):
T = 2π√(m/k) (in seconds)
The natural frequency and time period are intrinsic properties of the system and determine how fast or slow the system oscillates under free vibration.
Detailed Explanation
Natural frequency is a vital concept in vibration analysis; it signifies how many oscillations per second a system can execute without external forces. The time period is the duration of one complete oscillation cycle. Both of these properties are deeply influenced by the mass of the system and the spring's stiffness. Realizing these relationships allows engineers to design structures that do not easily resonate with external forces, such as earthquakes.
Examples & Analogies
If you think of a swing again, the natural frequency would tell you how many times the swing completes a full forward and backward swing in a given timeframe. If the chains are shorter (stiffer), it will swing faster than if they are longer (more flexible).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Free Vibration: Oscillation without external forces post-disturbance.
-
SDOF System: A mechanical model with one mass and spring, in one-dimensional motion.
-
Natural Frequency: Oscillation rate derived from mass and stiffness characteristics.
-
Equation of Motion: Governs the dynamics of vibrating systems, focusing on displacement and its derivatives.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A pendulum swinging after being pushed.
-
A mass on a spring oscillating when released from an initial position.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the mass jumps and starts to sway, the spring pulls back, it saves the day!
📖 Fascinating Stories
-
Imagine a toy on a spring. If you pull it back and let it go, it dances back and forth without a care – that’s free vibration in action.
🧠 Other Memory Gems
-
Remember 'FAST' - Free vibration means Always Simple Task (SDOF system).
🎯 Super Acronyms
SDOF
- Single Direction
- One Frequency.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Free Vibration
Definition:
The motion of a mechanical system when it vibrates naturally without the influence of external forces.
-
Term: Single Degree of Freedom (SDOF) System
Definition:
A simplified mechanical model with one mass that can oscillate in one direction, governed by a spring's stiffness.
-
Term: Natural Frequency (ωₙ)
Definition:
The rate at which a system oscillates in free vibration, determined by its mass and stiffness.
-
Term: Equation of Motion
Definition:
A mathematical representation of the dynamics of a vibrating system, often expressed as mx¨(t) + kx(t) = 0.
-
Term: Damping
Definition:
The process through which energy is dissipated in a vibrating system, affecting its amplitude over time.