Logarithmic Decrement (δ)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Logarithmic Decrement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will discuss logarithmic decrement, a measure for assessing the damping in vibrating systems. Can anyone tell me what damping means in this context?

Does it refer to how quickly a system loses energy?

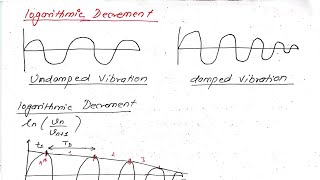
Exactly! Damping indicates how the amplitude of oscillation changes over time as energy is dissipated. The logarithmic decrement helps us quantify this change. The formula is δ = (1/n) * ln(x(t)/x(t+nT)).

What do the variables in that formula represent?

Good question! In the formula, n is the number of cycles of oscillation, and T is the time period. x(t) and x(t+nT) are the amplitudes measured at two different times.
Application of Logarithmic Decrement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Logarithmic decrement is particularly useful in experimental modal analysis. Does anyone know what that is?

Isn't it a method of testing how structures respond to vibrations?

That's correct! In testing, engineers disturb a structure and then measure its response, which helps in finding damping ratios. By using logarithmic decrement, we can estimate how quickly oscillations decay, which is critical for ensuring the stability of structures.

So, it helps prevent issues like resonance?

Exactly! Understanding damping helps us design structures that can withstand dynamic loads, like earthquakes.
Calculating Logarithmic Decrement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's do a quick calculation to reinforce our understanding. Suppose we have a mass-spring system and find that after 3 cycles, the amplitude has changed from 4 units to 2 units. How would we calculate the logarithmic decrement?

Using the formula, n would be 3, and the amplitudes would be 4 and 2, right?

Correct! Do you remember what T is here?

Well, T doesn't actually factor directly into the decay comparison since it's the same for both measurements, so it cancels out in the formula.

Well done! Now, what is the calculation?

So, δ = (1/3) * ln(4/2) = (1/3) * ln(2).

Great job! This approach helps hone our understanding of how damping behaves as we test different systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces logarithmic decrement as a key metric in assessing damping in systems undergoing oscillations. It explains how to calculate it by comparing amplitudes from different cycles and highlights its application in experimental modal analysis.
Detailed
Logarithmic Decrement (δ)
Logarithmic decrement is a vital concept for measuring damping in mechanical systems, particularly in the context of vibrations. It quantifies how the amplitude of oscillation decreases over time as the system dissipates energy. The formula used to calculate logarithmic decrement is:
\[ δ = \frac{1}{n} \ln\left( \frac{x(t)}{x(t+nT)} \right) \]
where:
- n = number of cycles between measurements,
- T = time period of oscillation,
- x(t) and x(t+nT) are the amplitudes at initial time and after n cycles, respectively.
This measurement is crucial in experimental modal analysis, where engineers aim to determine the damping characteristics of structures and materials. Understanding the logarithmic decrement aids in predicting the system's response under dynamic load conditions and assists in designing structures with appropriate damping properties.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Logarithmic Decrement
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Logarithmic decrement is used to measure damping in systems by evaluating the rate at which amplitude decays:
\[ \delta = \ln \left( \frac{x(t)}{x(t+nT)} \right] \]
Where:
- n = number of cycles
- T = time period
- x(t), x(t+nT) = amplitudes at different times
Detailed Explanation
Logarithmic decrement (δ) quantifies how quickly the amplitude of vibration in a system diminishes over time. It is expressed mathematically as the natural logarithm of the ratio of the amplitudes of a wave at two different points in time, separated by 'n' cycles of oscillation. This is important because it allows engineers and scientists to evaluate the damping characteristics of vibrating systems—how quickly they lose energy and stabilize after disturbance.
Examples & Analogies
Imagine swinging on a swing set. When you first push the swing, it goes high with a large amplitude (the height of the swing). As time passes, each time it swings back and forth, it gets lower until it stops. The logarithmic decrement measures how quickly the swing's height (amplitude) decreases with each swing.
Parameters in the Logarithmic Decrement Formula
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Where:
- n = number of cycles
- T = time period
- x(t), x(t+nT) = amplitudes at different times
Detailed Explanation
The formula involves key parameters. 'n' refers to how many complete cycles of vibration have occurred, which affects how far apart the two amplitude measurements are in time. 'T' is the time it takes for one complete cycle of oscillation. The amplitudes 'x(t)' and 'x(t+nT)' represent the height or distance from the rest position of the vibrating system at the two measured points. Understanding these parameters is crucial for accurately calculating damping.
Examples & Analogies
Think of a basketball player shooting hoops. Each time they take a shot (one cycle), they see how far the ball goes. If the ball goes significantly lower with each successive shot, the player can gauge how their shooting might be improving or degrading over time. Similarly, the Logarithmic Decrement helps analyze how a system's amplitude decreases with each 'shot' or cycle.
Applications of Logarithmic Decrement
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
It is useful in experimental modal analysis for damping estimation of real structures.
Detailed Explanation
Logarithmic decrement has crucial applications, especially in experimental modal analysis, which is a method used to determine the dynamic properties of structures. By measuring the decay of vibrations, engineers can estimate how effectively a structure will dampen vibrations—critical for assessing its safety and performance during dynamic events like earthquakes.
Examples & Analogies
Consider a dentist using a slow drill for precision work. This drill’s operation is smooth and controlled, allowing for fine-tuning. Similarly, engineers use Logarithmic Decrement to fine-tune structures to ensure they can withstand vibrations without failing—a careful balance between stability and safety.
Key Concepts
-
Logarithmic Decrement: A measure of how amplitude decreases over cycles, crucial for understanding damping.
-
Damping: The reduction of amplitude in oscillation due to energy loss.
-
Modal Analysis: A method to assess a structure’s vibrational characteristics.
Examples & Applications
If a bridge's vibration amplitude decreases from 20 mm to 10 mm over three cycles, the logarithmic decrement gives engineers insight into how quickly the bridge dissipates vibrational energy and aids in preventing potential resonance issues.
In an experimental setup, measuring the decay of a pendulum's swing over multiple swings can yield its damping characteristics through logarithmic decrement calculations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Log decrement's rate will show,
Stories
Imagine a swing that slows as you push it. Each swing loses energy until it stops, just like an amplitude that diminishes, helping illustrate how logarithmic decrement measures this loss in a vibrating system.
Memory Tools
D for Damping, L for Logarithmic, D for Decrement - 'D-L-D' to remember when measuring energy loss.
Acronyms
Remember 'LAD' for Logarithmic Amplitude Decay! Logarithmic for the formula, Amplitude for what we're measuring, and Decay for its diminishing character.
Flash Cards
Glossary
- Damping
The process by which oscillations decay over time due to energy loss.
- Logarithmic Decrement (δ)
A measure of amplitude decay in an oscillating system, calculated using the logarithmic ratio of two amplitudes over a number of cycles.
- Amplitude
The maximum extent of a vibration or oscillation, measured from the position of equilibrium.
- Modal Analysis
A technique used to determine the dynamic response of structures subjected to vibrational forces.
Reference links
Supplementary resources to enhance your learning experience.
