Base Excitation and Response
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Base Excitation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to talk about base excitation and response. Can anyone tell me what they think base excitation might refer to?

Is it when the ground shakes and affects how buildings move?

Exactly! Base excitation occurs when the ground movement, such as during an earthquake, impacts the structure. The ability of structures to withstand these forces is crucial in engineering.

How do engineers figure out how much a building will move?

Great question! Engineers use mathematical models, and we will explore the equations that describe this in detail.
Mathematical Model of Base Excitation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The equation for a structure experiencing base excitation is: mx¨(t) + cx˙(t) + kx(t) = -my¨(t). Can anyone tell me what each symbol means?

m is mass, c is damping, and k is stiffness, right?

Exactly! And y¨(t) is the ground acceleration. This equation helps us understand how the structure responds relative to ground motion.

What happens when the structure is moving with the ground?

Good observation! That’s where we define the relative motion—let's note that down for our understanding.
Relative Displacement and Response Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When analyzing base excitation, we look at relative displacement, which we define as x_r = x - y. This means we're focusing on how much the structure moves relative to the ground. Can anyone think why this might be important?

Because we need to know how much the building shifts compared to the ground to ensure it doesn’t fall over?

Exactly! Analyzing shifts is crucial for safety. The response can be expressed as x_r(t) = X sin(ωt - ϕ), where X is the amplitude and ϕ is the phase angle.

How does knowing the amplitude help us?

Knowing the amplitude allows us to predict the structural response and make informed decisions in the design process. It aids in ensuring structures can withstand dynamic loads.
Significance of Base Excitation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In summary, understanding base excitation is vital for designing earthquake-resistant structures. Why do you think this is critical?

Because a lot of buildings can be damaged or even collapse during earthquakes.

Exactly! By analyzing how structures respond to base motion, we can develop safer designs and mitigate risks associated with earthquakes.

So our equations essentially help save lives?

Yes, they play a critical role. Let's make sure to remember how to analyze and design our structures based on these principles!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Base excitation refers to the response of structures subjected to forces caused by ground movement, such as during earthquakes. This section describes the mathematical framework for modeling this interaction, focusing on the equation of motion, relative displacement, and dynamic responses of structures under such conditions.
Detailed
Base Excitation and Response
In the context of earthquake engineering, structures often experience what is termed as base excitation, where ground acceleration (such as from an earthquake) affects the motion of structures directly. The governing equation for a structure with base excitation can be expressed as:
$$ mx¨(t) + cx˙(t) + kx(t) = -my¨(t) $$
Here, y¨(t) represents the ground acceleration. By assuming a sinusoidal form for ground motion, e.g., \( y(t) = Y \sin(\omega t) \), we can analyze the response of the structure. The relative displacement is defined as: \( x_r = x - y \), and leads to the solution for the relative displacement of the structure being:
$$ x_r(t) = X \sin(\omega t - ϕ) $$
This section highlights how the responses of structures can amplify when subjected to base excitation and outlines the significance of this analysis for engineering resilient structures to earthquakes.
Youtube Videos


![[BCT2025 Webinar] Long Period Ground Motion in Earthquake – its Impacts, Measures and Effects 1](https://img.youtube.com/vi/0lGZlFHEbS4/mqdefault.jpg)

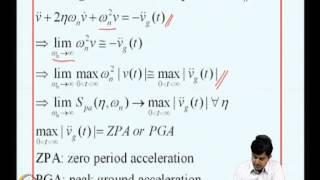





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Base Excitation Model
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In earthquake engineering, structures often experience base excitation, modeled as:
mx¨(t)+cx˙(t)+kx(t)=−my¨(t)
Where y¨(t) is ground acceleration (e.g., due to an earthquake). If y(t)=Y sin(ωt), the analysis follows similarly using relative motion formulation.
Detailed Explanation
The equation demonstrates how a structure responds when its base moves, particularly during an earthquake. Here, 'm' is the mass of the structure, 'c' is the damping coefficient, and 'k' is the stiffness. The term 'y¨(t)' represents the ground acceleration, which is a key factor during seismic events. If the ground is shaking in a sinusoidal manner, we can express the ground displacement as 'y(t)=Y sin(ωt)'. In this scenario, we analyze how the structure behaves relative to the moving ground.
Examples & Analogies
Imagine a tree swaying in the wind. If the ground shakes (like a strong gust), the tree's base moves while the branches sway less directly with the wind. Similarly, in buildings, the base movement during an earthquake means the structure needs to respond appropriately to avoid damage, just like how the tree's structural integrity depends on its response to winds.
Relative Displacement
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The solution is:
x (t)=X sin(ωt−ϕ)
r r
Where
x r=x−y
is the relative displacement between mass and base.
Detailed Explanation
This solution illustrates how the actual displacement 'x(t)' of the structure can be understood in relation to the ground motion. The formula shows that the total response 'x(t)' is a function of both the driving force and the relative motion of the structure against the moving base. Here, 'X' is the amplitude of the response, and 'ϕ' is the phase angle indicating how much the structural response lags behind the ground movement. The calculation of 'x r=x−y' lets us find the displacement of the structure relative to the base.
Examples & Analogies
Think of two people dancing at a party, one on a moving platform (the base) and the other standing still on the ground. The dancer on the platform experiences their movement (the base motion) and must adjust their dance steps accordingly. The relative position between the two dancers shows how much the dancer on the platform has to move to stay in sync, similar to how buildings need to adjust their positions during ground motion.
Key Concepts
-
Base Excitation: The movement imposed on a structure by ground motion.
-
Relative Displacement: The difference in position between the structure and the ground.
-
Ground Acceleration: The acceleration experienced by the ground during seismic activity.
-
Phase Angle: Represents lag or lead between the input force and the resulting motion.
-
Amplitude: The extent of motion or vibration experienced by the structure.
Examples & Applications
In an earthquake, buildings sway due to ground motion, which is modeled as base excitation.
A bridge designed with base isolation will allow its foundation to move independently from ground motion.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the ground shakes and quakes, structures sway; base excitation is what we say.
Stories
Imagine a tall building during an earthquake. As the ground shakes, the building sways in response, but it’s not just moving by itself — it’s influenced by how much the ground itself moves. This is the essence of base excitation.
Memory Tools
Remember the acronym A-B-G-P (Amplitude, Base Excitation, Ground acceleration, Phase angle) when studying these concepts!
Acronyms
Use the acronym BERG
Base Excitation
Relative Displacement
Ground Acceleration to recall key terms.
Flash Cards
Glossary
- Base Excitation
The motion experienced by structures due to ground movement, particularly in seismic events.
- Relative Displacement
The difference between the displacement of a structure and the displacement of the ground.
- Ground Acceleration
The rate of change of velocity of ground movement, typically measured during seismic events.
- Phase Angle
The angle that represents the phase difference between the structure's response and the applied ground motion.
- Amplitude
The maximum extent of a vibration or oscillation, measured from the position of equilibrium.
Reference links
Supplementary resources to enhance your learning experience.
