Use of Damping in Controlling Harmonic Response
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damping Types
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing how different types of damping affect the response of structures. Can anyone tell me what viscous damping is?

Isn't viscous damping when the damping force is proportional to how fast something is moving?

Exactly! Viscous damping is proportional to the velocity. Can someone explain what Coulomb damping represents?

Coulomb damping is related to friction between surfaces, right? It doesn’t depend on velocity?

Correct! Coulomb damping is nonlinear and varies with the direction of motion. And what about hysteretic damping?

That type loses energy depending on the material properties during each cycle of loading.

Precisely! Remember that understanding these types helps engineers design better structures.

In summary, viscous damping is linear, Coulomb is nonlinear due to friction, and hysteretic damping depends on the material.
Importance of Damping in Structures
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, let's delve into why damping is essential in structural engineering. Why do you think we need to reduce peak amplitudes?

To prevent structural failure during events like earthquakes or high vibrations?

Great point! Reducing peak amplitudes helps avoid excessive vibrations. How does damping aid in energy dissipation?

Damping helps convert kinetic energy into heat, allowing the structure to manage energy better.

Correct! This energy dissipation contributes significantly to maintaining the stability of the structure. Can anyone summarize the role of the damping ratio?

The damping ratio indicates how quickly a system returns to rest and helps shape the response near resonance.

Exactly! To summarize, damping reduces peak response, dissipates energy, and stabilizes structural response.
Analyzing Harmonic Response with Damping
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's explore how different damping ratios affect the system response. Why do you think a high damping ratio is beneficial?

Because it could lead to lower peak responses during resonance.

That's right! Higher damping ratios help in stabilizing the system. Can anyone provide an example of a real-world application of damping?

Like tuned mass dampers in high-rise buildings to reduce sway during wind loads?

Exactly! These dampers work to minimize vibrations and improve comfort and safety. What’s the key takeaway about damping?

Damping is crucial for controlling structural response under dynamic loads!

Well said! To conclude, damping mechanisms are vital for enhancing the resilience of structures.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Understanding damping is crucial for structural engineers as it affects how structures respond to harmonic excitations. This section covers various damping types, including viscous, Coulomb, and hysteretic damping, and explains their significance in reducing peak amplitudes, increasing energy dissipation, and stabilizing the response of structures under dynamic loading.
Detailed
Use of Damping in Controlling Harmonic Response
Damping is a fundamental concept in structural dynamics that plays a critical role in controlling the response of structures subjected to harmonic excitations. There are several types of damping mechanisms, each with distinct characteristics:
1. Types of Damping in Structures
- Viscous Damping: This type is proportional to the velocity of the system and is commonly used in theoretical models.
- Coulomb Damping: Caused by friction, this damping is nonlinear and varies with the direction of motion.
- Hysteretic Damping: This type is material-dependent, involving energy loss during each cycle of loading.
2. Role of Damping
Damping plays several vital roles in the response of structures:
- Reduces Peak Amplitude: Damping helps control and lower the peak response near resonance frequencies, which is crucial for preventing excessive vibrations that can lead to structural failure.
- Increases Energy Dissipation: It enhances the ability of the structure to dissipate energy, thus reducing the risk of damage under dynamic loading conditions.
- Stabilizes the Response: A well-damped structure exhibits more stable behavior under dynamic loads, leading to a more predictable and safe response during earthquakes or machinery vibrations.
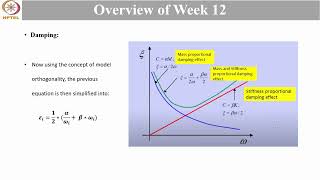
The damping ratio (ξ) is central to understanding these concepts, as it influences how quickly the transient effects of harmonic excitation decay and shapes the system's response near resonance.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Types of Damping in Structures
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Viscous Damping: Proportional to velocity, common in theoretical analysis.
• Coulomb Damping: Due to friction, nonlinear.
• Hysteretic Damping: Material-dependent, energy lost during each cycle.
Detailed Explanation
Damping can be categorized into three main types:
1. Viscous Damping: This type occurs when the resistance to motion is proportional to the velocity. Imagine pushing a car; the faster you push, the harder it is to push. This form is common in theoretical models as it simplifies calculations while still representing real-world behaviors.
- Coulomb Damping: This occurs due to friction between surfaces. When two objects slide against each other, friction resists their movement in a nonlinear manner. It’s like trying to slide a heavy box across rough carpet; at first, it may not move, but once it does, it suddenly slides more easily, illustrating a nonlinear characteristic.
- Hysteretic Damping: This is material-dependent and relates to how a material behaves under cyclic loading. During this process, some energy is lost in each cycle due to internal friction. Think of a spring: when you stretch and release it, it doesn’t return fully to its original position because some energy is 'lost' as heat.
Examples & Analogies
Consider dampers in a car. When you hit a bump (like a sudden force), the springs and absorbers (dampers) work together to absorb that shock. Viscous damping in the fluid-filled shocks helps control the bounce by applying resistance proportional to how fast the car moves (velocity). Coulomb damping is akin to how the tires grip the road, potentially causing a nonlinear response when you start or stop suddenly.
Role of Damping
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Reduces peak amplitude near resonance.
• Increases energy dissipation.
• Helps stabilize the response under dynamic loading.
Damping ratio ξ plays a central role in governing how quickly the system’s transient effects decay and how sharply the system responds near resonance.
Detailed Explanation
Damping is crucial for managing structural responses to dynamic loads. Here’s how:
1. Reduces Peak Amplitude: When a structure is excited by a periodic force (like wind or an earthquake), damping helps lower the highest levels of movement ('peak amplitude') that can occur, particularly near resonance.
- Increases Energy Dissipation: Damping allows the system to convert kinetic energy into heat, which means less energy remains within the structure to cause further movement or vibrations. In short, it helps 'use up' vibrational energy effectively.
- Stabilizes Response: A good damping system means that when a sudden force occurs, the structure doesn’t react erratically but instead recovers smoothly. This stabilization is vital for safety and integrity during dynamic loads, like those from an earthquake.
The damping ratio (ξ) is a key factor influencing how quickly a system returns to steady state after being disturbed. A higher damping ratio means that transient effects diminish quickly, leading to a more stable and responsive structure.
Examples & Analogies
Think of damping like a seatbelt in a car. In the event of a sudden stop (like hitting the brakes hard), the seatbelt slows you down safely, reducing the impact (the peak amplitude of your forward motion) and helping you stay in your seat. Similarly, damping in structures helps 'slow down' vibrations to prevent potential damage, just like a seatbelt protects passengers.
Key Concepts
-
Damping Types: Various damping mechanisms, including viscous, Coulomb, and hysteretic, impact structural response differently.
-
Role of Damping: Damping reduces peak amplitudes, dissipates energy, and stabilizes the structural response under dynamic loads.
-
Damping Ratio (ξ): A key parameter that determines the decay rate of transient effects and influences system behavior near resonance.
Examples & Applications
Damped oscillators in buildings equipped with tuned mass dampers to minimize vibrations from wind.
High-rise structures that utilize viscous dampers to control sway during seismic events.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When damping is high, vibrations die, keeping structures safe as time goes by.
Stories
Imagine a pendulum swinging freely, and as soon as you apply a dampening force, you see it calm down and stabilize, avoiding potential overturning, just like in buildings.
Memory Tools
Remember 'VCH' for damping types: Viscous, Coulomb, Hysteretic.
Acronyms
DAMP stands for Damping's Amplitude Management Principle.
Flash Cards
Glossary
- Viscous Damping
A type of damping where the damping force is proportional to the velocity of the moving object.
- Coulomb Damping
Damping that arises due to friction, which is nonlinear and depends on the direction of motion.
- Hysteretic Damping
Damping dependent on material behavior, causing energy loss during each loading cycle.
- Damping Ratio (ξ)
A dimensionless measure that describes how oscillations in a system decay after a disturbance.
Reference links
Supplementary resources to enhance your learning experience.
