Harmonic Excitation in Multi-Degree-of-Freedom (MDOF) Systems
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Governing Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're focusing on the governing equations for MDOF systems. The equation includes mass, damping, and stiffness matrices. Can anyone tell me why we would need these matrices?

Because they summarize the physical properties of the system!

Exactly! The matrices allow us to account for each degree of freedom in our analysis. Now, what does the general form of the harmonic excitation equation look like?

It's like \([M]{X¨} + [C]{X˙} + [K]{X} = {F} sin(ωt)\)!

Fantastic! Remember, each term contributes to how the system responds dynamically. Let's dive deeper into how these matrices affect our analysis.
Modal Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To simplify our MDOF systems, we use modal analysis. Can anyone share what this process involves?

It decouples the system into modes that act like SDOF systems!

Exactly right! This decoupling process makes it easier to analyze each mode's behavior. How does modal superposition come into play here?

It combines different modes to get the total response of the system.

Well said! Modal superposition is crucial for understanding how complex systems respond during seismic events. Let's summarize: we decompose the system, analyze the individual modes, and then combine them for the total picture.
Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss practical applications of our theoretical insights. Why is harmonic excitation analysis important in engineering, particularly in seismic design?

It helps in designing structures to withstand earthquakes by predicting how they will behave under dynamic loads!

Right again! Engineers utilize these analyses to ensure structures can dissipate energy and remain safe during events like earthquakes. Can anyone think of a specific design approach that benefits from these analyses?

One example could be tuning mass dampers to reduce vibrations!

Spot on! Such designs directly link our principles to real-world applications in structural integrity and safety.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The discussion on harmonic excitation in MDOF systems highlights the governing equations that account for multiple degrees of freedom, the process of modal analysis that simplifies the complexity, and importance in real-world applications such as seismic design.
Detailed
Harmonic Excitation in Multi-Degree-of-Freedom (MDOF) Systems
In structures with multiple degrees of freedom, harmonic excitation can significantly affect the dynamic response. The governing equations describe the motion of such systems, represented as:
$$
[M]{X¨} + [C]{X˙} + [K]{X} = {F} sin(ωt)
$$
Where \([M]\), \([C]\), and \([K]\) are the mass, damping, and stiffness matrices respectively, ensuring that the equations encapsulate the behavior of MDOF systems under harmonic loads.
Modal Analysis
To analyze the complex system dynamics effectively, modal analysis is utilized. This involves decoupling the system into modal coordinates where each mode behaves similarly to a single-degree-of-freedom (SDOF) system. The method of modal superposition constructs the total response by combining these individual modes, making modal analysis crucial for seismic design and response spectrum analysis, illustrating the correlation between theory and practical applications in structural dynamics.
Youtube Videos








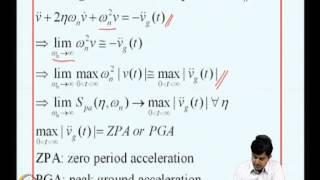

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Governing Equations for MDOF Systems
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When dealing with real structures, multiple degrees of freedom must be considered.
The governing equation for a multi-degree-of-freedom (MDOF) system subjected to harmonic excitation is:
[M]{X¨ }+[C]{X˙ }+[K]{X}={F }sin(ωt)
Detailed Explanation
In this chunk, we're discussing how multi-degree-of-freedom (MDOF) systems are modeled. The equation represents how the system's mass, damping, and stiffness interact under harmonic loads. Here,
- [M] is the mass matrix, which accounts for the mass distribution across the system,
- [C] is the damping matrix, which represents energy dissipation through material properties or connections,
- [K] is the stiffness matrix, which captures how much the system resists deformation,
- {X} is a vector of displacements, indicating how far each degree of freedom moves,
- {F} represents the applied harmonic force, and ω is the frequency of the excitation.
This means that when the system experiences a sinusoidal force, its multiple points of movement (degrees of freedom) need to be evaluated collectively as opposed to individually.
Examples & Analogies
Imagine a symphony orchestra, where each musician represents a degree of freedom in the system. Just like each musician needs to play together in harmony to create a beautiful piece of music, each degree of freedom in the MDOF system needs to work together to respond accurately to harmonic excitation. If one musician plays out of sync, the whole performance can be disrupted, similar to how improper responses in an MDOF structure can lead to structural failure.
Modal Analysis in MDOF Systems
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In MDOF systems, modal analysis involves decoupling the system using modal coordinates. Each mode behaves like an SDOF system, and modal superposition is used to construct total response. This approach is crucial in seismic design and response spectrum analysis.
Detailed Explanation
Here we introduce modal analysis, which breaks down the complex behavior of an MDOF system into simpler parts. The idea is to find the 'modes' of vibration, which are the specific patterns in which the system can naturally oscillate. By transforming the system into modal coordinates:
- We treat each mode as if it were its own simpler system (like single-degree-of-freedom systems), making calculations easier.
- The overall response of the structure is then constructed by adding together responses from each mode (modal superposition). This technique is especially important in designing buildings to withstand earthquakes, as it allows engineers to predict how buildings will behave under seismic forces by analyzing these fundamental modes of vibration.
Examples & Analogies
Think of modal analysis like breaking a complex recipe into simpler steps. If you have a complicated dish that requires many ingredients and techniques, it can be daunting. But if you focus on preparing each component (mode) of the dish separately and then combine them at the end, the cooking process becomes manageable and efficient. Similarly, in structural engineering, analyzing each mode helps ensure the overall structure can withstand any external forces it faces.
Key Concepts
-
Mass, Damping, and Stiffness Matrices: Fundamental components of MDOF systems which together dictate the response to dynamic loading.
-
Modal Analysis: A method essential for breaking down complex systems into simpler, manageable parts for analysis.
-
Modal Superposition: The process of combining individual modal responses to produce the overall system response.
-
Harmonic Excitation: A type of periodic force critical in evaluating the dynamic response of structures.
Examples & Applications
When designing a skyscraper in an earthquake-prone area, engineers must analyze the harmonic responses of the building's various modes using MDOF principles.
In assessing the seismic integrity of a bridge, modal analysis is used to measure and modify its response under harmonic loading conditions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To build a strong structure, check each mode, in every quake's load, the right response is showed.
Stories
Imagine an engineer standing atop a bridge, who listens to the whispers of each design. By tuning into the natural frequencies, he ensures that each harmonic load elegantly dances without stress.
Memory Tools
M-C-S for MDOF: Mass, Damping, Stiffness - key players in the dynamic show.
Acronyms
M.A.R.E.
Modal Analysis Reduces Errors in harmonic excitation response.
Flash Cards
Glossary
- MultiDegreeofFreedom (MDOF) Systems
Systems characterized by multiple independent movements or degrees of freedom, often requiring complex analysis to determine dynamic response.
- Governing Equations
Mathematical equations that describe the motion of dynamic systems under various forces.
- Modal Analysis
A technique used to analyze the natural frequencies and mode shapes of a system, allowing for simplified modeling of complex systems.
- Modal Superposition
A method where the total response of a system is expressed as the sum of its individual modal responses.
Reference links
Supplementary resources to enhance your learning experience.
