Limitations of Linear Harmonic Analysis
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Assumption of System Linearity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing the significant limitations of linear harmonic analysis. The first major limitation is the assumption of system linearity. Can anyone tell me why this might be critical in real-world scenarios?

Because structures can behave differently when loads get too high, right?

Exactly! At large amplitudes or during strong earthquakes, materials may yield and behave nonlinearly. This can lead to catastrophic failure if we assume the structure behaves linearly. Remember the acronym 'BIG'—B for Behavior changes, I for Increased loads, and G for Gradual yield.

Can we design structures to avoid reaching that point?

Absolutely, it's crucial to consider these design parameters in order to enhance safety.

What tools do engineers use in those scenarios?

Excellent question! Engineers often rely on more sophisticated methods such as nonlinear analysis methods.

To summarize: linearity assumes predictable behavior, but once we exceed limits, the real behavior can change drastically.
Material Nonlinearity and Joint Behavior
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In our next session, let's delve into material nonlinearity and joint behavior. How can these factors influence structural dynamics?

Maybe cracks or slippage can make things worse?

Right. Cracking under tension or joint slippage leads to uneven forces distributing within the system, which our linear models may not account for adequately.

So, does that mean we can't just use linear harmonic analysis in every situation?

Correct! We need to analyze these materials under realistic conditions and consider nonlinear models for more accurate representations.

Could software help simulate these scenarios?

Yes, simulation software can model these complex behaviors more accurately. Always remember, analyzing the limits of materials is as critical as the design itself.

To summarize, as materials and joints behave nonlinearly, relying solely on linear analyses could lead to unsafe designs.
Soil-Structure Interaction
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s discuss soil-structure interaction. How does this fit into our limitations of linear harmonic analysis?

Soil foundational behavior affects how structures respond during earthquakes, right?

Exactly, soil stability and movement can introduce additional degrees of freedom which our standard models may not account for. This interaction can drastically modify a structure’s response.

So does that mean engineers need to factor in soil analysis too?

Yes! Engineers need to consider soil characteristics in dynamic assessments, often conducting separate analyses to assess these interactions.

So, we can’t rely just on linear models if the soil changes the picture.

Spot on! In conclusion, the soil and structure work together, and we must analyze both to capture accurate responses.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the limitations of linear harmonic analysis, highlighting its assumptions of system linearity, the impact of material properties, and the complications introduced by soil-structure interactions. It emphasizes the need for more advanced methods in practical seismic design.
Detailed
Limitations of Linear Harmonic Analysis
Linear harmonic analysis is a cornerstone in understanding structural dynamics under harmonic excitation, yet it possesses significant limitations. This section outlines three primary constraints of this analytical method:
- Assumption of System Linearity: Linear harmonic analysis operates under the assumption that the system behavior remains linear even at large amplitudes and during strong earthquakes. However, real-world structures may exhibit nonlinear behavior due to material yielding and geometric changes when subjected to substantial forces.
- Material Nonlinearity and Joints: The characteristics of construction materials, such as cracking and joint slippage, can significantly alter the dynamics of a structure. Those changes impact the structural responses, which linear models may fail to capture accurately.
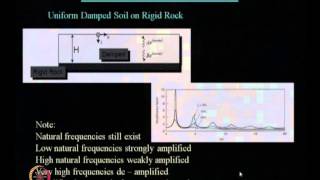
- Soil-Structure Interaction: The interaction between soil and structures introduces additional complexities and degrees of freedom that typical linear harmonic analyses do not account for sufficiently. This can lead to inaccuracies in predicting how structures behave under seismic loading, necessitating the incorporation of more advanced analytical techniques in practical engineering applications.
In conclusion, while linear harmonic analysis provides a foundational understanding, real-world applications often require additional methods such as time history analysis, nonlinear pushover analysis, and probabilistic seismic hazard analysis (PSHA) to achieve accurate predictions of structural responses.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Assumption of System Linearity
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
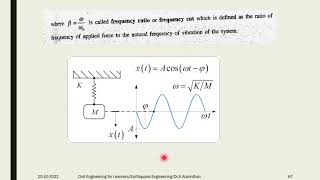
- Assumes system linearity, which may not hold at large amplitudes or during strong earthquakes.
Detailed Explanation
Linear harmonic analysis is based on the assumption that the response of a system to external forces is directly proportional to the applied forces. This works well for small forces and displacements where materials behave predictably. However, at large amplitudes (big forces or movements), materials can behave nonlinearly, meaning their response is not directly proportional to the input, which can lead to inaccurate predictions about how structures will behave during severe events like strong earthquakes.
Examples & Analogies
Think of a rubber band. When you stretch it gently, it stretches proportionally to the force you apply—this is linear behavior. But if you stretch it too far, it might snap or lose its ability to return to its original shape—this is a nonlinear behavior. Similarly, buildings can behave like the rubber band when exposed to extreme forces.
Influence of Material Nonlinearity and Joints
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Material nonlinearity, joint slippage, and cracking may alter system dynamics.
Detailed Explanation
In real-world structures, materials can have different mechanical properties that change under stress. For instance, concrete can crack under pressure, and metal joints can slip or loosen. These behaviors alter how the entire structure responds to forces. Linear harmonic analysis does not account for these complexities, which means predictions might be overly simplified or incorrect, especially in extreme conditions.
Examples & Analogies
Imagine a flexing metal ruler. If it bends too much, you will notice it starts to change shape permanently, similar to how cracked concrete behaves. When analyzing structures using linear assumptions, we might ignore that some parts of the structure won't perform as expected under high stress.
Soil-Structure Interaction
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Soil-structure interaction often introduces additional degrees of freedom and nonlinearity.
Detailed Explanation
When a building is constructed on soil, the interaction between the soil and the structure can significantly affect how the building behaves under dynamic loads like earthquakes. The soil itself can shift, settle, or change its properties with stress, introducing more complexity into the system. This relationship isn't adequately captured by simple linear models, which might miss crucial impacts of soil movement on the stability and safety of structures.
Examples & Analogies
Think of a tall tree in your backyard. If there’s a strong wind, the tree may sway, and if the ground is loose or muddy from rain, it could lean or even fall. Similarly, buildings on unstable soil might suffer more extensive damage during an earthquake than what linear analysis predicts.
Combining Analyses for Better Predictions
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- In real-world seismic design, harmonic response is often used in combination with:
- Time history analysis
- Nonlinear pushover analysis
- Probabilistic seismic hazard analysis (PSHA)
Detailed Explanation
To improve predictions and ensure safety during seismic events, engineers often combine linear harmonic analysis with other methods, such as time history analysis, which looks at how structures respond over time to specific seismic events. Nonlinear pushover analysis evaluates how structures will perform when pushed beyond their elastic limits. Probabilistic seismic hazard analysis considers the likelihood of different earthquake scenarios occurring. Together, these methods provide a more comprehensive understanding of structural behavior under dynamic loads.
Examples & Analogies
It's like preparing for a storm. Instead of just checking one weather forecast (linear analysis), you look at multiple forecasts, history of storms in your area, and real-time data from satellites (time history, nonlinear, and probabilistic analyses) to prepare your home better for whatever weather might come your way.
Key Concepts
-
System Linearity: Assumes proportional response but can fail at large amplitudes.
-
Material Nonlinearity: Real materials may not display linear characteristics during significant loading.
-
Joint Behavior: Changes in joints lead to nonlinear response under extreme forces.
-
Soil Interaction: External forces can alter the response due to interaction with foundational soil mechanics.
Examples & Applications
The Tacoma Narrows Bridge collapse exemplifies how linear assumptions can fail under dynamic loading.
A structure designed with linear analysis may experience excess deformation during ground motion due to soil instability.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In solid ground structures abide, but if soil moves, they may slide.
Stories
Once in a stable town, they built a bridge strong and wide. But when the earthquakes rolled, the soil shifted, and the bridge tried to hide.
Memory Tools
Remember 'SEAM' for limitations: Soil, Elasticity, Amplitude, Material.
Acronyms
Use 'LENS' to recall key limitations
Linearity
Elasticity
Nonlinearity
Soil interaction.
Flash Cards
Glossary
- Linearity
The assumption that a system's response is directly proportional to the applied load.
- Material Nonlinearity
Behavior of materials where their stiffness varies with the amount of load applied.
- Joint Slippage
Loss of stiffness at structural connections leading due to excessive forces.
- SoilStructure Interaction
The influence of soil properties and behavior on the structural response during dynamic loading.
Reference links
Supplementary resources to enhance your learning experience.
