Equation of Motion for Harmonic Excitation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Equation of Motion for SDOF Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re discussing the equation of motion for single-degree-of-freedom systems subjected to harmonic excitation. The equation is expressed as mx¨(t) + cx˙(t) + kx(t) = F₀ sin(ωt). Can anyone help me identify what each term in this equation represents?

I think *m* is mass, right? What about the others?

Correct! *m* is the mass of the system. *c* is the damping coefficient, which represents how much energy is dissipated in the system, and *k* is the stiffness, which describes how the system resists deformation. *x(t)* is the displacement. Can you remember what *F₀* and *ω* are?

Are they the amplitude and frequency of the harmonic force?

Exactly! *F₀* is the amplitude of the harmonic force and *ω* is the forcing frequency. This equation forms the basis for understanding how structures behave under dynamic loads.
Understanding the Solutions of the Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

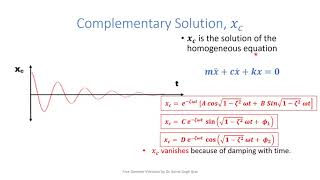
Now that we know the equation, let’s discuss its solutions. This second-order differential equation has two parts: the homogeneous solution and the particular solution. Who can tell me what these solutions represent?

Is the homogeneous solution the transient response?

Yes, exactly! The homogeneous solution handles how the system responds initially before settling down. Can someone tell me what the particular solution represents?

I think it’s the steady-state response of the system?

Spot on! The particular solution describes the long-term behavior of the system after all transients have died out. As we move on, this distinction will help us analyze various dynamic problems.
Significance of Harmonic Excitation in Structural Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can anyone explain why understanding harmonic excitation is so critical in the field of structural dynamics?

I guess it's because structures often face periodic forces like vibrations from machines or earthquakes?

Absolutely! Harmonic excitation gives us a baseline understanding of how structures react to periodic loads, which is essential for designing buildings and bridges. And remember, our understanding will aid in evaluating the safety and stability of structures.

So, it’s really important to prevent resonance, right?

That's correct! Avoiding resonance and knowing how to manage dynamic loads keeps structures safe and functional. Great job connecting the concepts!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Key concepts in this section include the general form of the equation of motion for harmonic excitation in single-degree-of-freedom systems, distinguishing between homogeneous and particular solutions while laying a foundation for understanding dynamic responses in structural engineering.
Detailed
In this section, we delve into the equation of motion for single-degree-of-freedom (SDOF) systems under harmonic excitation, which serves as a cornerstone for analyzing dynamic structural response. The equation is expressed as:
$$mx¨(t)+cx˙(t)+kx(t)=F_{0} sin(ωt)$$
where m represents mass, c is the damping coefficient, k is stiffness, and x(t) denotes the displacement over time. The parameters F₀ and ω are notable as the amplitude and frequency of the harmonic force, respectively.
An important aspect of the solution to this second-order differential equation divides it into two components: the homogeneous solution (which describes the transient response) and the particular solution (which captures the steady-state response). This framework is crucial for understanding the behavior of structures under dynamic loads like seismic activity or machinery vibrations.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Equation of Motion
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The general form of the equation of motion for a single-degree-of-freedom (SDOF) system subjected to a harmonic force is:
mx¨(t)+cx˙(t)+kx(t)=F sin(ωt)
Where:
- m = mass
- c = damping coefficient
- k = stiffness
- x(t) = displacement as a function of time
- F = amplitude of harmonic force
- ω = forcing frequency
- ωₙ = natural frequency of the system.
Detailed Explanation
In this equation, we have three main components which contribute to how a system will respond to external vibrations:
1. Mass (m): This is the resistance of the system to acceleration. A larger mass means the system will be less responsive to the external force.
2. Damping Coefficient (c): Damping is what dissipates energy, reducing oscillations over time. Higher damping means the vibrations will die out faster.
3. Stiffness (k): This is how rigid the system is. A stiffer system will resist deformation more strongly.
The equation shows how these three factors combine with the applied force (F) to determine the motion (x(t)) of the system over time (t).
Examples & Analogies
Think of this equation like a playground swing. The mass of the swing is the seat (the mass), the ability of the swing to stop swinging represents damping (when you push it lightly and it slows down), and how far the swing can move up from its resting position relates to stiffness (the direction of where you push the swing). Each part influences how the swing behaves after being pushed.
Solutions to the Differential Equation
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The solution of this second-order differential equation consists of two parts:
1. Homogeneous solution (transient response)
2. Particular solution (steady-state response)
Detailed Explanation
When we solve the differential equation of motion, we divide the solution into two components:
1. Homogeneous Solution: This part represents the system's response after an initial disturbance, such as a push. It describes how the system oscillates due to its own characteristics without ongoing external forces.
2. Particular Solution: This portion addresses how the system behaves under the continuous influence of an external force, which, in this case, is harmonic or sinusoidal.
Together, these solutions give a complete picture of how the structure will behave over time.
Examples & Analogies
Imagine you're on a swing again. When someone gives you a big push (the external force), your swing moves in a certain way (the particular solution). After that push is gone, your swing will continue to move back and forth on its own because of momentum (the homogeneous solution). Together, they describe the entire experience of swinging.
Key Concepts
-
Equation of motion for SDOF systems: It encompasses mass, damping, and stiffness components.
-
Homogeneous solution: Represents transient response of the system.
-
Particular solution: Represents steady-state response of the system under harmonic forces.
Examples & Applications
An example of a SDOF system could be a mass-spring-damper setup, where the mass oscillates under the influence of a sinusoidal force.
In engineering applications, harmonic excitations can occur in buildings due to vibrations from HVAC systems or machinery.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Mass, damping, stiffness, make them right, in motion they dance, day or night.
Stories
Imagine a swing at the playground, with kids playing – it goes left, right, but comes back to rest after the push, representing harmonic motion.
Memory Tools
M-C-S-F (Mass-Damping-Stiffness-Force) - Remember the key parameters of our equation!
Acronyms
SDOF - Single-Degree-of-Freedom system is key in our discussions.
Flash Cards
Glossary
- SingleDegreeofFreedom (SDOF) System
A dynamic system that can be described using a single coordinate to define its motion.
- Harmonic Excitation
A periodic force that varies sinusoidally with time, often represented by F₀ sin(ωt).
- Damping Coefficient (c)
A parameter that quantifies the damping effect in the system, influencing its energy dissipation.
- Stiffness (k)
A measure of the resistance offered by the system against deformation.
- Natural Frequency (ω_n)
The frequency at which a system tends to oscillate when not subjected to external forces.
- Mass (m)
The quantity of matter in a body, influencing its dynamic response.
- Displacement (x(t))
The change in position of a point on a structure with respect to time.
Reference links
Supplementary resources to enhance your learning experience.
