Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The equations of motion for MDOF systems describe how the system responds dynamically to external forces. The standard form is [M]{u¨(t)} + [C]{u˙(t)} + [K]{u(t)} = {F(t)}, where [M] is the mass matrix. Can anyone tell me what the mass matrix represents?
It represents the distribution of mass within the system, which affects how the system moves.
Exactly! And can anyone explain the roles of the damping and stiffness matrices?
The damping matrix [C] affects how energy is dissipated, while the stiffness matrix [K] relates to how the system resists deformation.
That's correct! So the total equation effectively captures the dynamic behavior of the structure due to forces—like those from an earthquake.
The Need for Decoupling
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, why do we need to decouple these equations? Why can't we just solve them directly?
It seems like solving a complex system with many equations would be really hard and time-consuming!
Exactly! By decoupling the equations, we simplify them. Each equation can then be solved individually. This is especially useful in the context of seismic analysis. Can anyone recall what modal analysis involves?
It’s about transforming the equations using eigenvectors to get independent equations.
Yes, and that leads us into understanding the properties of orthogonality and the role of modal matrices!
The Concept of Modal Transformation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s dive into modal transformation. We replace our displacement vector {u(t)} with modal coordinates {q(t)} using a modal matrix [Φ]. Can anyone tell me what this matrix includes?
It contains the eigenvectors, which represent the mode shapes of the system!
Correct! By applying this transformation, we can derive the decoupled equations. What happens to the mass and stiffness matrices after transformation?
They become diagonalized matrices. This makes solving them much easier.
Yes! You all are getting it! The diagonalization simplifies our calculations significantly!
Orthogonality Conditions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Orthogonality is a fundamental property that greatly assists in our analysis. Can anyone describe the mass and stiffness orthogonality properties?
For mass orthogonality, the integral of the product of different modes with the mass matrix equals zero, right?
Exactly! This means the modes do not interfere with each other during vibration. And what about stiffness orthogonality?
Similar idea! It states modes are orthogonal with respect to the stiffness matrix.
Correct! Understanding these conditions is crucial for decoupling and valid modal analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the mathematical representation of the equations of motion for linear elastic multi-degree-of-freedom systems, highlighting the role of mass, damping, and stiffness matrices in understanding dynamic response under excitation. The transformation of coupled equations into independent equations via modal analysis is critical for efficient earthquake engineering.
Detailed
In multi-degree-of-freedom (MDOF) systems, the equations of motion are expressed as a set of coupled second-order differential equations, presented in matrix form as [M]{u¨(t)} + [C]{u˙(t)} + [K]{u(t)} = {F(t)}, where [M], [C], and [K] represent the mass, damping, and stiffness matrices, respectively. Here, {u(t)} denotes the displacement vector and {F(t)} represents external forces acting on the system. Due to the complexity associated with solving these coupled equations directly, the process of decoupling becomes essential. The use of modal analysis facilitates transformation to independent scalar equations that correspond to different modes of vibration, enabling simplified calculations in dynamic analyses, particularly concerning seismic events. Understanding these equations is foundational for effective seismic analysis and design of structures subjected to dynamic loading.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Form of Equations of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
[M]{u¨(t)}+[C]{u˙(t)}+[K]{u(t)}={F(t)}
Detailed Explanation
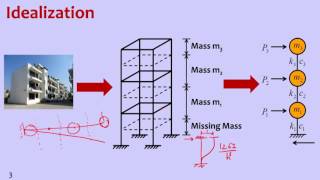
The equation presented is the general form of the equations of motion for a linear elastic multi-degree-of-freedom (MDOF) system. Here, \[ [M] \] represents the mass matrix, \[ [C] \] is the damping matrix, \[ [K] \] is the stiffness matrix, \{u(t)\} is the displacement vector describing the positions of the system's components, and \{F(t)\} is the force vector, which represents any external forces acting on the system, such as those from seismic activity. This equation is a matrix equation that encompasses 'n' degrees of freedom and is actually a system of 'n' second-order coupled differential equations.
Examples & Analogies
Imagine a group of friends trying to coordinate their movements while playing a game. Each friend (representing a degree of freedom) has to adjust their position based on the decisions of the group (external forces). The equations represent how the whole group moves together, adjusting for their individual weights (mass), how they dampen each other's movements (damping), and the overall structure of the game (stiffness).
Components of the Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
• [M] is the mass matrix
• [C] is the damping matrix
• [K] is the stiffness matrix
• {u(t)} is the displacement vector
• {F(t)} is the force vector (including earthquake forces)
Detailed Explanation
This section provides clarity about each component in the equations of motion. The mass matrix \[ [M] \] quantifies the inertia of the system, indicating how the mass is distributed across various components. The damping matrix \[ [C] \] reflects how energy is dissipated, impacting how vibrations decrease over time. The stiffness matrix \[ [K] \] represents the rigidity of the system, indicating how much resistance is offered against deformation when external forces are applied. The displacement vector \{u(t)\} represents how much each part of the system moves from its original position over time, while the force vector \{F(t)\} accounts for the external influences, such as forces from ground motion during an earthquake.
Examples & Analogies
Think of a trampoline. The mass matrix is like the weight of the people jumping on it; the more weight, the more it sinks. The damping matrix is like the air resistance; it slows you down while bouncing. The stiffness matrix is about how tightly the trampoline is stretched. The displacement vector shows how much the trampoline surface drops when weight is applied, and the force vector includes all the jumping (external forces acting on it).
Nature of the Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a system of n second-order coupled differential equations.
Detailed Explanation
The equations formed are second-order because they involve the second derivative of displacement, which relates to acceleration in dynamics. Being coupled means that the equations are interdependent; the motion of one component affects the motion of another. This coupling makes it more complex to analyze the system's behavior, as these equations need to be solved together rather than independently.
Examples & Analogies
Consider a dance group where each dancer's movement is dependent on the others; if one dancer slows down or changes direction, it affects the entire formation. Similarly, in our equations, each degree of freedom (like each dancer) influences the others, making it necessary to analyze how all pieces work together rather than just looking at them one at a time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
[M]: The mass matrix is fundamental in determining inertial effects.
-
[C]: The damping matrix is crucial for understanding energy dissipation.
-
[K]: The stiffness matrix describes the resistance to deformation.
-
Decoupling: A process that simplifies the equations of motion for easier analysis.
-
Modal Analysis: A technique to transform the equations using modal coordinates and eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A building with 3 floors can be modeled as a MDOF system with specific mass distribution where the mass matrix [M], stiffness matrix [K], and damping matrix [C] are defined based on structural properties.
-
An analysis of a bridge under earthquake loading using the equations of motion helps engineers predict the necessary structural reinforcements.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass matrices hold the weight, Damping’s loss can’t wait, Stiffness keeps the structure straight, In motion's dance, they all relate!
📖 Fascinating Stories
-
Imagine a building as a dancer in a dynamic ballet, where the mass matrix keeps her grounded, the damping matrix softens her landings, and the stiffness matrix helps her maintain control in her performance.
🧠 Other Memory Gems
-
Remember the acronym MDS: M for Mass, D for Damping, S for Stiffness — these matrices are the backbone of analyzing motion!
🎯 Super Acronyms
Use the acronym FMD for the equations
- F: represents external forces
- M: for the mass matrix
- and D for the damping matrix.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: [M]
Definition:
Mass matrix representing the mass distribution of a system.
-
Term: [C]
Definition:
Damping matrix that characterizes how energy is dissipated in a system.
-
Term: [K]
Definition:
Stiffness matrix that quantifies a system's resistance to deformation.
-
Term: {u(t)}
Definition:
Displacement vector representing the positions of the system's nodes at any time.
-
Term: {F(t)}
Definition:
External force vector acting on the system, typically including earthquake forces.
-
Term: [Φ]
Definition:
Modal matrix containing eigenvectors that are used for transformation to modal coordinates.
-
Term: Modal Analysis
Definition:
A technique used to transform coupled equations of motion into decoupled equations using mode shapes.
-
Term: Orthogonality
Definition:
A property indicating that different mode shapes do not interact or influence each other's dynamics.