Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Modal Equations for Undamped Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss modal equations specifically for undamped systems. Can anyone remind me what a modal equation looks like?
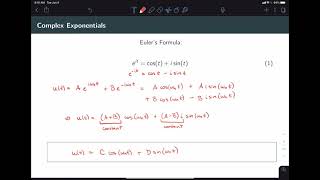
Isn't it something like q¨(t) + ω²qᵢ(t) = F∗(t) for each mode?
Exactly! This equation represents the motion of our system when it is not subject to damping. Now, why do you think these systems behave in such a harmonic way?
Because with no damping, the oscillations continue indefinitely, like a pendulum without friction!
That's a great analogy, Student_2! Remember, this simplicity can make the mathematics easier for us—like following the 'Harmonic Rule' for undamped systems.
Methods to Solve the Modal Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've established what the modal equations are, let's focus on how we can solve them. What methods do you think we could use?
I remember something about Duhamel’s Integral? Is that one?
Yes, that's correct, Student_3! Duhamel’s Integral helps find the response for arbitrary loading conditions. Have any of you heard about the Convolution Integral?
It's like figuring out how a system responds over time based on its past inputs!
Right again! This shows us the relationship between input and output in a linear time-invariant system. Finally, we have the Laplace Transform, which converts our ODEs into simpler algebraic forms to solve them.
So, we can use various tools to handle different situations and types of loads?
Precisely! Different methods allow us to adapt to different scenarios in dynamics.
Importance of Solving Undamped Modal Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's discuss why solving these equations is crucial, especially in structural and earthquake engineering. How do these solutions aid engineers?
They help in predicting how structures will respond during seismic activities, right?
Exactly, Student_2! By understanding these dynamics, we ensure buildings can withstand earthquakes. What would happen if we ignored these equations?
Buildings might collapse, or we could over-engineer them unnecessarily!
Spot on! It’s about finding that balance between safety and material efficiency. Thus, mastering these techniques is vital for engineers.
Applications in Real-World Scenarios
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's consider real-world applications of solving undamped modal equations. Can anyone think of a specific scenario where this knowledge is invaluable?
In designing buildings in earthquake-prone areas, we need to predict how they will behave under seismic forces.
Absolutely! And when we apply the solutions, we ensure safety and longevity of structures. This leads us to understand the concept of modal superposition we’ll tackle later!
So applying these equations correctly can literally save lives during earthquakes?
Yes! This is why engineers must focus on accurate analyses, and using modal methods allows for that precision.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In the context of undamped systems, this section highlights that the modal equations become purely harmonic and can be solved using techniques such as Duhamel’s integral, convolution integral, and Laplace transform. Understanding these methods is vital for analyzing seismic responses effectively.
Detailed
Special Case: Undamped Systems
In systems without damping, the modal equations derived from the dynamics of multi-degree-of-freedom (MDOF) systems take on a purely harmonic nature, represented as:
q¨(t) + ω²qᵢ(t) = F∗(t)
for each mode i.
These second-order ordinary differential equations (ODEs) can be solved using several mathematical techniques:
1. Duhamel’s Integral: This integral is useful for obtaining the system response due to arbitrary loading conditions over time.
2. Convolution Integral: This method allows for the computation of the output of a linear time-invariant (LTI) system based on its input and its impulse response.
3. Laplace Transform: The Laplace transform is a powerful tool for solving ODEs, particularly when dealing with arbitrary loadings, as it transforms differential equations into algebraic equations.
Understanding these solution methods is crucial for engineers and analysts working in fields such as earthquake engineering, where simplified models of undamped structural systems are frequently used.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Undamped Modal Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For undamped systems, the modal equations are purely harmonic:
q¨(t)+ω2q_i(t)=F∗(t)
Detailed Explanation
In this chunk, we are introduced to the nature of the equations that govern undamped systems. An undamped system implies that there are no energy losses in the form of heat or friction. The equations presented are second-order ordinary differential equations (ODEs), indicating that the system's behavior can be described purely in terms of harmonic motion. Here, q¨(t) represents the acceleration of the modal coordinate at time t, while ω² is the square of the natural frequency of the system, and F∗(t) denotes the external force acting on the system in its modal form.
Examples & Analogies
Think of a perfectly frictionless swing. When you push it, it swings back and forth forever without slowing down. This absence of damping is similar to our undamped systems—energy does not dissipate, allowing the swing (or the system's response) to oscillate indefinitely.
Methods for Solving Undamped Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These are second-order ODEs that can be solved using:
- Duhamel’s Integral
- Convolution Integral
- Laplace Transform (for arbitrary loading)
Detailed Explanation
This chunk outlines various mathematical methods for solving the second-order ordinary differential equations associated with undamped systems.
- Duhamel's Integral allows for the solution of non-homogeneous problems by relating them to a homogeneous problem.
- Convolution Integral is used to evaluate the system response caused by an arbitrary input over time, effectively blending the effects of past inputs.
- Laplace Transform is a technique that translates differential equations into algebraic equations, making it easier to solve for complex loading scenarios.
Examples & Analogies
Imagine organizing a concert. Each method is like a different way to get the sound from the stage to the audience. Duhamel’s Integral is like a live feed, capturing changes in real-time. The Convolution Integral is like playing back recordings of past songs layered together, creating a new experience. The Laplace Transform is akin to translating live music into sheet music, making it much simpler to understand and rearrange for different instruments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Undamped Systems: Systems that continue oscillating indefinitely without loss of energy.
-
Modal Equation: A representation of the motion of a system's mode under harmonic conditions.
-
Duhamel’s Integral: A solution method for dynamic response under arbitrary loading.
-
Convolution Integral: A technique for understanding system output in response to an input signal.
-
Laplace Transform: A mathematical approach for simplifying differential equations into algebraic forms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Duhamel’s Integral to find the response of an undamped system to a sudden load applied at time t=0.
-
Applying Laplace Transform to solve a second-order ODE that represents the motion of a spring-mounted mass without damping.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the realm of undamped sway, the motions never fade away.
📖 Fascinating Stories
-
Imagine a playground swing that goes on forever; just like that swing, undamped systems continue to oscillate without slowing down, demonstrating infinite motion until acted upon.
🧠 Other Memory Gems
-
To remember the methods: 'DCL' — Duhamel, Convolution, Laplace - all help solve undamped dynamics!
🎯 Super Acronyms
The acronym 'HARD' can remind you of 'Harmonic undamped Response Dynamics.'
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Undamped Systems
Definition:
Systems that do not exhibit damping, leading to perpetual oscillations.
-
Term: Modal Equation
Definition:
An equation that describes the behavior of a specific mode in a dynamic system.
-
Term: Duhamel’s Integral
Definition:
A method for solving non-homogeneous linear differential equations.
-
Term: Convolution Integral
Definition:
An operation that expresses the output of a system as a function of its input and impulse response.
-
Term: Laplace Transform
Definition:
A technique used to transform ordinary differential equations into algebraic equations.