Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
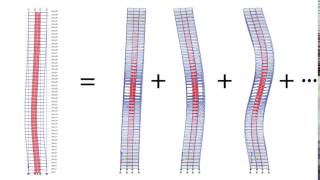
Today, we are going to discuss mode shapes. Can anyone tell me what a mode shape is?
Is it the shape that a structure takes when it vibrates?
Exactly! Mode shapes represent the various ways a structure can vibrate. They are crucial for understanding dynamic behavior under loads like earthquakes. Now, why do you think we might want to normalize these mode shapes?
Maybe to simplify calculations when analyzing their effects?
That's correct! Normalization helps ensure that each mode shape individually interacts properly with the mass matrix in calculations.
The Normalization Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's look at the equation representing normalization: \( \phi_i^T [M] \phi_i = 1 \). Can anyone explain what this means?
It means that when we multiply the mode shape by the mass matrix and then by the same mode shape again, we get 1.
Precisely! This condition ensures that each mode shape maintains a standardized weight relative to the system's mass, allowing for better accuracy in dynamic analysis.
Application of Normalization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
By normalizing mode shapes, we transition from more complex equations to simpler forms like \( \ddot{q}_i(t) + \omega_i^2 q_i(t) = F^*(t) \). Why do you think this simplification is valuable?
It helps in quickly solving the dynamic equations without getting bogged down in complicated calculations!
Absolutely! This simplification allows engineers to compute and predict structural behavior more efficiently under different scenarios, including seismic responses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The normalization of mode shapes allows for simplifying modal equations related to dynamic systems. By ensuring each mode shape relates to the mass matrix in a defined manner, we can further streamline the analysis and ensure the proper computation of dynamic behaviors in multi-degree-of-freedom systems.
Detailed
Normalization of Mode Shapes
In structural dynamics, particularly when analyzing multi-degree-of-freedom (MDOF) systems under dynamic loads like seismic activities, it becomes essential to normalize mode shapes. The normalization of mode shapes refers to setting the condition that the inner product of a mode shape vector with respect to the mass matrix equals one:
\[ \phi_i^T [M] \phi_i = 1 \]
This ensures that each mode shape contributes appropriately to the modal analysis, yielding a simplified form of the modal equations:
\[ \ddot{q}_i(t) + \omega_i^2 q_i(t) = F^*(t) \]
where \( \omega_i \) signifies the natural frequency of the i-th mode. The significance of this process lies in facilitating computational efficiency and clarity within dynamic analyses, leading ultimately to better informed engineering decisions regarding structural stability under seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Normalization with Respect to Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mode shapes can be normalized with respect to mass:
ϕT[M]ϕ = 1
i i
Detailed Explanation
Normalization of mode shapes means adjusting them so that their contribution to the overall mass is standardized. In this case, the equation ϕT[M]ϕ = 1 indicates that when you multiply the transposed mode shape vector ϕ with the mass matrix [M] and then with ϕ again, the result should equal 1. This is vital because it sets a reference for comparing different mode shapes consistently. By ensuring that each mode shape has this property, it helps in simplifying the calculations that come later in the modal analysis.
Examples & Analogies
Think of normalizing mode shapes like adjusting the weight of ingredients in a recipe so that they're all in a consistent format. If you're baking and you want to ensure that the cake's layers all bake evenly, you'd measure out each ingredient to scale properly. Just as the normalized weights ensure a consistent and tasty cake, normalized mode shapes guarantee that the analysis of dynamic responses is consistent and accurate.
Simplification of Modal Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This simplifies the modal equations further:
q¨(t) + ω²q (t) = F∗(t)
i i i i
Where ω is the natural frequency of the ith mode.
Detailed Explanation
After normalizing the mode shapes, the modal equations take on a simpler form. The equation q¨(t) + ω²q (t) = F∗(t) describes the behavior of each mode of vibration as a simple harmonic oscillator. In this equation, q¨(t) is the acceleration of the mode, ω is its natural frequency, and F∗(t) is the modal force acting on that mode. This format is easier to solve compared to the coupled equations from before because each mode can be analyzed independently of the others.
Examples & Analogies
Imagine riding a swing. Each swing has a natural frequency at which it swings back and forth most comfortably. If we treat each swing as a separate entity, we can predict how high it will go based on how hard you push it (the force applied). In the same way, once modes are normalized, we can predict the response of each 'swing' (or mode) in isolation, making complex dynamics much easier to evaluate.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Normalization of Mode Shapes: Setting the inner product of mass matrix and mode shape to 1 facilitates simplified calculations.
-
Mass Matrix: A critical component in the equations of motion representing mass distribution.
-
Natural Frequency: Associated with each mode, impacts the dynamic response of the structure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The normalization of mode shapes can be applied in a 3-story building model to derive its dynamic characteristics.
-
An example can be seen in seismic analysis where normalizing helps in calculating the reaction of buildings during earthquakes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When mode shapes we set just right, mass equals one, now let’s take flight.
📖 Fascinating Stories
-
Imagine a musician tuning a guitar. Each string's frequency must be precise, similar to correctly normalizing mode shapes, where each mode resonates perfectly with its mass.
🧠 Other Memory Gems
-
NORM for Normalizing Mode Shapes: N = Necessary, O = Optimal energy, R = Resulting checks, M = Making contributions clear.
🎯 Super Acronyms
M for Mass, N for Normalization, and S for Shapes. MNShapes keep our dynamics in place.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Shape
Definition:
The shape that a structure takes at specific frequencies during vibration modes.
-
Term: Normalization
Definition:
The process of adjusting mode shapes so that they fulfill a specific condition for accurate analysis.
-
Term: Mass Matrix
Definition:
A matrix representing the mass distribution of a system, used in dynamic analysis.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.