Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Modal Truncation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss modal truncation. Can anyone explain what it might mean?
Isn't it about reducing the number of modes we use in analysis?
Correct! Modal truncation involves retaining only the significant modes during analysis. Why do you think we do this?
To simplify the calculations, I assume?
Exactly! It's crucial in seismic analysis where we might deal with many degrees of freedom.
Criteria for Modal Truncation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about how we determine which modes to retain. Can anyone share any criteria?
Modal mass participation factor is one, right?
Exactly, great point! The modal mass participation factor helps identify the contribution of each mode to the total response. What else?
The cumulative effective mass ratio?
Spot on! These ratios help ensure we capture the most impactful modes.
Practical Implications of Modal Truncation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's consider real-world applications. How does modal truncation help engineers in practice?
It speeds up the analysis process, right? We can run simulations faster?
Precisely! By focusing on just the key modes, engineers save time and resources. Anyone else want to elaborate on this?
And it helps to simplify the modeling process, so we can better understand the structure's behavior!
Exactly! Simplified models are easier to work with and can still provide valuable insights.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
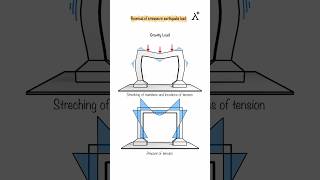
Modal truncation focuses on the selection of a limited number of significant vibrational modes (typically the first three to six) that contribute most to the response of the system during seismic analysis. This method is essential to efficiently analyze multi-degree-of-freedom systems while ensuring that key dynamic characteristics are captured.
Detailed
Modal Truncation
In structural dynamics, particularly in the context of earthquake engineering, not all modes contribute equally to a building's response to seismic forces. Modal truncation is a technique aimed at simplifying the analysis by retaining only the first few dominant modes, which are identified based on their modal mass participation factors and cumulative effective mass ratios. Typically, retaining three to six modes is sufficient to achieve a good approximation of the actual behavior of the structure during seismic events.
The selection of these modes is guided by their participation in the overall system response, ensuring that the analysis remains computationally efficient while still capturing the essential dynamics of the structure. This approach significantly reduces complexity in modeling and computations, allowing engineers to focus on critical factors influencing the structural performance during earthquakes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Modal Truncation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In practice, not all modes contribute significantly to the response, especially in seismic analysis. Modal truncation involves retaining only the first few (usually 3–6) dominant modes, depending on their participation in the total response.
Detailed Explanation
Modal truncation is a technique used in dynamic analysis of structures to simplify the calculation process. In many cases, not all vibrational modes—a natural frequency and the corresponding shape of deformation—affect the overall response of a structure significantly. Researchers found that only the initial few modes (typically 3 to 6) are responsible for the majority of the dynamic response during an earthquake or other loadings. Thus, by truncating or ignoring higher modes, we reduce computational effort while maintaining a good approximation of the system's behavior under dynamic loads.
Examples & Analogies
Think of a musical instrument, like a guitar. The fundamental frequency (the first mode) is the loudest note you hear when the guitar is strummed. Although there are higher overtones (higher modes), they don't contribute as much to the overall sound. Just as a guitarist can focus on the fundamental note for simplicity, engineers can focus on the primary modes of vibration to effectively analyze a structure's response.
Criteria for Modal Truncation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Criteria include:
• Modal Mass Participation Factor
• Cumulative Effective Mass Ratio
Detailed Explanation
When applying modal truncation, engineers use specific criteria to determine which modes to keep. The Modal Mass Participation Factor tells us how much each mode contributes to the overall mass of the structure's dynamic response. Only modes that significantly affect the total response are retained. Additionally, the Cumulative Effective Mass Ratio helps to understand if a sufficient portion (like 90% or 95%) of the mass is represented by the selected modes. If the retained modes account for a large part of the system response, we are justified in ignoring the rest for analysis.
Examples & Analogies
Imagine packing for a trip. You can only take a limited amount of luggage, so you pick the essential items that will give you the most benefit. By evaluating what is the most useful—including clothes based on weather and activities—you maintain functionality while keeping your luggage manageable. Similarly, engineers select only the most significant modes to keep the analysis efficient and focused on the most impactful aspects of a structure's behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modal Truncation: A method to simplify dynamic response analysis by retaining only important vibrational modes.
-
Modal Mass Participation Factor: Indicates the contribution of each mode to the total dynamic behavior.
-
Cumulative Effective Mass Ratio: Helps determine the number of modes needed to capture significant response.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In seismic analysis, focusing on the first three modes often captures 90% of the structural response, allowing for efficient computations.
-
Using modal truncation, an engineer can model a 20-storey building by analyzing only 5 significant modes rather than all 20.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To truncate, you don’t want to overstate, three to six modes will relate; it saves the time we can calculate!
📖 Fascinating Stories
-
Imagine a librarian overwhelmed by thousands of books. She decides to only keep the top-rated books that everyone loves, making her library much easier to manage while still offering great reads. This is like modal truncation — keeping only essential modes!
🧠 Other Memory Gems
-
For modal truncation, think 'MPC' - Modal Participation Criteria: Modal mass participation factor and cumulative effective mass ratio.
🎯 Super Acronyms
REC (Retain, Evaluate, Check) — Retain significant modes, Evaluate contributions (participation factor), Check cumulative impact.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Truncation
Definition:
A technique used to simplify dynamic analysis by retaining only the significant modes of a system.
-
Term: Modal Mass Participation Factor
Definition:
A measure of how much each mode contributes to the overall dynamic response of a system.
-
Term: Cumulative Effective Mass Ratio
Definition:
A ratio that indicates the summed contribution of selected modes to the total mass of the system.