Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Modal Participation Factors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will dive into the concept of modal participation factors. These factors let us know how much each mode contributes to the response of a system during seismic activity.
Why do we need to consider the contributions of different modes?
Great question! Each mode represents a unique way the structure can vibrate. Understanding their contributions helps engineers assess which modes are significant when designing for earthquakes.
How is the modal participation factor calculated?
It's calculated using the formula Γᵢ = (ϕᵢ^T[M]{r}) / (ϕᵢ^T[M]ϕᵢ). This allows us to compare the influence of each mode's shape with the overall mass.
Can you explain what {r} represents in the formula?
{r} is typically a vector of ones, representing uniform loading conditions, such as ground motion. This ensures that our analysis incorporates the effects of seismic excitation accurately.
In summary, understanding the modal participation factor gives us insights into the essential modes needed for precise seismic analysis.
Applications of Modal Participation Factors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s explore how modal participation factors are used in practice. Why do you think assessing modal contributions is crucial in structural design?
It sounds important when analyzing how structures would behave during an earthquake.
Exactly! Engineers use modal participation factors to identify which vibration modes should be included in dynamic analysis to capture the structure's response accurately.
What happens if we don't account for important modes?
Not accounting for significant modes can lead to unsafe designs or underestimating the potential dynamic responses of a structure under seismic loads. This could result in serious structural failures.
How many modes should we usually consider?
Typically, we aim to include enough modes to account for 90 to 95% of the total effective mass. This ensures reliability and safety in designs.
In conclusion, modal participation factors streamline our design process and enhance our understanding of seismic responses.
Effective Modal Mass and Its Importance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s connect the modal participation factor with effective modal mass today. Why do you think it's important to understand both?
I guess effective modal mass helps us quantify the contribution of each mode in a different way.
Absolutely! The effective modal mass is given by M_eff,i = Γᵢ^2 · ϕᵢ^T[M]ϕᵢ. It combines the participation factor with the mode shape to assess each mode's contribution.
How does this relate to the overall structural performance?
When evaluating the total response of a structure, assessing effective modal mass helps ensure that critical modes are included in the analysis.
So, this means that if some modes are not contributing significantly, we might not need to consider them to simplify our analysis?
Exactly! This is part of what we call modal truncation, where we focus on the dominant modes for efficient analysis.
In summary, effective modal mass provides a more comprehensive view of mode contributions, enhancing our analysis accuracy.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the modal participation factor, which helps evaluate the importance of each vibration mode in response to ground motion by comparing the contributions based on the mass matrix. It is key for determining effective modal mass and for successful modal analysis in earthquake engineering.
Detailed
Modal Participation Factors
The modal participation factor, denoted as Γᵢ, is a critical component in understanding the dynamic response of structural systems to seismic excitations. It is calculated using the expression:
\[ Γᵢ = \frac{ϕᵢ^T[M]{r}}{ϕᵢ^T[M]ϕᵢ} \]
Where:
- ϕᵢ: The i-th mode shape vector;
- [M]: The mass matrix;
- {r}: The influence vector also typically represented as a vector of ones, signifying uniform ground motion.
The significance of this factor lies in its ability to determine which modes significantly contribute to the overall dynamic behavior of the structure. A larger participation factor indicates that the given mode plays a greater role in the dynamic response under seismic loads.
Additionally, understanding this factor is essential for evaluating the effective modal mass (M_eff,i) for each mode, expressed as:
\[ M_{eff,i} = Γᵢ^2 · ϕᵢ^T[M]ϕᵢ \]
This helps in ensuring that enough modes have been included in the modal analysis to account for a sufficient percentage of the total mass—often 90% or 95%—thereby ensuring the reliability of the seismic design.
Youtube Videos
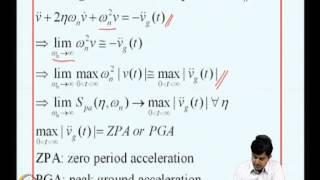
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Modal Participation Factor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The modal participation factor Γ quantifies how much each mode contributes to the response of the system due to ground motion. It is calculated as:
ϕT[M]{r}
Γ = i
ϕT[M]ϕ
i i
Detailed Explanation
The modal participation factor (Γ_i) measures the contribution of the i-th mode shape (ϕ_i) to the overall response of a structural system when affected by ground motion. This is significant in seismic analysis as it helps engineers determine which modes are essential for predicting how a structure reacts during an earthquake. The formula shows the ratio of two quantities: the numerator involves the interaction between the mode shape and the mass matrix multiplied by the influence vector, while the denominator normalizes this interaction with respect to the mass associated with that mode.
Examples & Analogies
Imagine a concert where different instruments represent different modes of vibration in a structure. Each instrument contributes to the overall sound, but not all equally. For instance, the drums might have a strong, pervasive influence that you can feel (high participation factor), while a violin might only be a subtle part of the orchestra (low participation factor). Understanding these contributions helps conductors (engineers) know which instruments (modes) are crucial for the music (structure) to resonate properly during a performance (earthquake).
Components of the Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
• ϕ : i-th mode shape vector
• [M]: Mass matrix
• {r}: Influence vector (usually a vector of ones for ground motion in one direction)
Detailed Explanation
In the equation for the modal participation factor, we have specific components that play crucial roles. The mode shape vector ϕ_i represents the shape or form of the i-th mode of vibration, capturing how the structure deforms during that mode. The mass matrix [M] contains information about the distribution of mass throughout the structure, affecting how forces act on it. Finally, the influence vector {r} usually consists of ones and indicates the direction of the ground motion's impact on the structure. This setup ensures that the modal analysis reflects how even just a unit ground motion will influence the system.
Examples & Analogies
Think of the components in this equation like the ingredients of a recipe to create a dish. The mode shape vector ϕ could be seen as the specific flavor profile you're creating (like herbs and spices), the mass matrix [M] is akin to the main ingredients (like chicken or tofu), and the influence vector {r} is your cooking method (baking or frying). Together, these components define what the final dish will taste like, just as they determine how the structure will respond to seismic forces.
Importance of Participation Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This factor helps determine which modes are important for a particular loading condition. Larger participation factors indicate higher contribution of the mode to the total dynamic response.
Detailed Explanation
Understanding the modal participation factors is crucial for ensuring that a structural analysis accurately reflects how the system behaves under seismic loading. If a mode has a high participation factor, it indicates that this mode will significantly influence how the structure will respond. Therefore, engineers can focus on these higher participation modes in their analysis, which makes the evaluation process more efficient and effective, optimizing design and safety measures.
Examples & Analogies
Consider a sports team where certain players have a more significant impact on the game's outcome than others. For instance, a star player (high participation factor) might consistently score goals, while a bench player (low participation factor) might only play during garbage time. Coaches (engineers) must recognize the star players and develop strategies around them, just as engineers should prioritize modes with higher participation factors to ensure structural integrity during seismic events.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modal Participation Factor: Represents the contribution of each mode during seismic loading.
-
Effective Modal Mass: Indicates the mass contributing to structural response from each mode.
-
Influence Vector: Used to assess loading conditions, typically consisting of ones.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a three-story building, if the first mode has a participation factor of 0.7 and the second mode has 0.3, the first mode contributes significantly more to the seismic response.
-
In a simple framework, the effective modal mass for the first mode might be calculated as 3 times greater than for the second, indicating its dominance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Factor, the modal participation leads to great anticipation; how each mode’s behavior is key to our foundation!
📖 Fascinating Stories
-
Imagine a tree swaying in the wind. Each branch shakes differently, much like modes during earthquakes. The most critical branches tell us how stable the tree is, aiding our design choices.
🧠 Other Memory Gems
-
Remember the acronym 'MICE' for Modal analysis: M - Modal Participation Factor, I - Influence Vector, C - Contribution of modes, E - Effective Modal Mass.
🎯 Super Acronyms
PEMDAS for the calculation of participation factor
- P: - Participation
- E: - Effective mass
- M: - Mode shape
- D: - Dynamics
- A: - Analysis
- S: - Seismic.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Participation Factor (Γᵢ)
Definition:
A measure quantifying the contribution of the i-th mode to the overall dynamic response of a structure subjected to seismic loading.
-
Term: Mode Shape (ϕᵢ)
Definition:
A vector that describes the deformation pattern of the structure at a specific frequency during vibration.
-
Term: Mass Matrix ([M])
Definition:
A matrix that represents the mass properties of the structure in its equations of motion.
-
Term: Influence Vector ({r})
Definition:
A vector typically consisting of ones that represents the distribution of forces acting on the system, especially during ground motion.
-
Term: Effective Modal Mass (M_eff,i)
Definition:
The mass associated with the i-th mode, indicating its contribution towards the total mass of the structure.