Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Overview of the Modal Superposition Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the Modal Superposition Method. Can anyone tell me what they think this method is used for?
Is it used to analyze how buildings respond during earthquakes?
Exactly! It primarily helps us simplify the analysis of dynamic systems, especially during seismic events. Why do we need to simplify these systems?
Because they can be really complicated and involve many interactions!
Right! The idea is to break down complex equations into simpler, independent equations for each mode of vibration. This way, we can analyze each mode separately.
So, if we can solve them separately, we can just add them up later?
Exactly! This brings up our modal superposition principle.
Can you explain that principle more?
Of course! It states that the total response of a system can be obtained by summing the individual modal responses. It's a core idea of modal analysis.
To remember this concept, think: 'Separate to Understand, Sum to Solve!'
In summary, the Modal Superposition Method helps us analyze complex dynamic responses by breaking them into simpler, manageable components.
Individual Modal Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s take a deeper look at how the individual modal equations are formed. What does the basic equation look like?
Is it similar to the general equation of motion we learned before?
Yes, it's quite similar! Each modal equation takes the form: $$ q¨(t) + 2ξ_i ω_i q˙(t) + ω^2_i q(t) = F^*(t) $$. What do each of these terms represent?
The \( ω_i \) is the natural frequency, and \( ξ_i \) is the damping ratio?
That's correct! The natural frequency indicates how quickly the system would oscillate, and the damping ratio tells us how much energy is lost over time. Any questions on how we apply these?
What about the \( F^*(t) \) term?
Great question! \( F^*(t) \) is the equivalent modal force acting on that mode. We solve for \( q(t) \) for each modal equation, and then we can combine them for the full response.
To help remember, think of \( q(t) \) as the 'quick answer' from each mode!
In summarizing, each modal equation describes how the system behaves under specific vibrations, factoring in natural frequency and damping.
Summing Modal Responses
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have individual modal equations, what do we do next?
We solve each modal equation and then add them together for the total response!
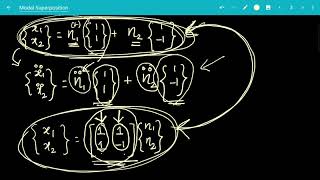
Exactly! We can express this as: $$ {u(t)} = Σ_{i=1}^n ϕ_i q_i(t) $$. Why is this summation necessary?
Because each mode contributes differently to the overall response, and we need them all!
Correct! Integrating all modes helps provide a complete picture of the structure's behavior during dynamic loading. Any confusion about combining these terms?
Do we always use all the modes in practice?
Great follow-up! While we analyze all modally relevant responses, often only a few dominant modes significantly influence the results; that’s where modal truncation comes into play.
To recap, after analyzing individual modal behaviors, we sum them to get the total response, reflecting all contributions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Modal Superposition Method involves decoupling dynamic systems into independent scalar equations, enabling the computation of individual modal responses. By summing these responses, the total response of multi-degree-of-freedom systems under dynamic loads, such as seismic forces, can be efficiently derived.
Detailed
Modal Superposition Method
The Modal Superposition Method is a powerful approach in structural dynamics for analyzing multi-degree-of-freedom (MDOF) systems under dynamic loads. This method becomes relevant after decoupling the modal equations of motion, which allows the total system analysis to be broken down into simpler, independent components.
- Individual Modal Equations: Each mode of vibration is treated as an independent scalar equation of the form:
$$ q¨(t) + 2ξ_i ω_i q˙(t) + ω^2_i q(t) = F^*(t) $$
Here, \( ξ_i \) represents the damping ratio and \( ω_i \) the natural frequency of the ith mode. The term \( F^*(t) \) denotes the modal force associated with each mode.
- Summing Modal Responses: Once each modal equation is solved, the total response of the system is reconstructed by summing up the contributions from all modes:
$$ {u(t)} = Σ_{i=1}^n ϕ_i q_i(t) $$
In this equation, \( {u(t)} \) represents the total displacement response vector, and \( ϕ_i \) are the modal shape vectors corresponding to each mode.
The Modal Superposition Method not only simplifies computations in structural dynamics but also makes it easier to conduct seismic analysis for complex structures, ensuring that significant dynamic behaviors are captured without excessive computational effort.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Scalar Modal Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once decoupled, each scalar modal equation can be solved individually:
q¨(t)+2ξωq˙(t)+ω²q(t)=F∗(t)
i i i i i i i
Where ξ is the damping ratio of the ith mode.
Detailed Explanation
This chunk discusses the individual modal equations that result from the decoupling process. In simple terms, once the complex system of equations is decoupled, we can treat each mode of vibration separately. Each scalar modal equation looks like a simplified form of a dynamic system, which includes terms for acceleration, velocity, and displacement. The damping ratio, indicated by ξ (xi), represents how oscillations in that mode either lose energy over time (damping) or continue too long (undamped). Understanding how to solve these equations gives insight into the behavior of each part of the structure during an event such as an earthquake.
Examples & Analogies
Imagine you are tuning a piano. Each string represents a different mode of vibration. When struck, each string vibrates individually while contributing to the overall sound. Similarly, in the modal superposition method, we analyze how each mode (string) responds separately to forces (strikes) before combining these responses to understand the whole piano's sound (the structure's behavior).
Total Response Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The total response of the system is then obtained by summing modal responses:
{u(t)}=Σϕ q(t)
i i
where n is the total number of modes considered in the superposition.
Detailed Explanation
After solving the individual modal equations, the next step is to determine the overall response of the structure. This is done through summation, where each mode's response, derived from the earlier equations, is added together. The result is {u(t)}, the total displacement vector of the structure due to all modes of vibration. The summation signifies that all modal contributions must be considered to fully understand how the entire structure reacts to seismic activity or any external forces.
Examples & Analogies
Think of constructing a team performance in a relay race. Each runner (modal response) contributes their time to the overall team score (total system response). When we add the times together, we can see how well the entire team performed based on each individual’s contribution. In structural dynamics, just like in the race, we need to consider every mode’s influence to get a complete picture of the system's behavior.
Modal Superposition Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is called the Modal Superposition Principle.
Detailed Explanation
The Modal Superposition Principle is the foundational concept behind how we analyze dynamic systems such as structures. It asserts that the overall behavior of the structure can be represented as a sum of its modes of vibration. Essentially, it's a formalization of the previous discussions, connecting the individual modal responses back to the overall structural response. This principle is key in understanding how complex systems can be simplified into manageable computations by focusing on individual modes.
Examples & Analogies
Imagine a large orchestra where each musician plays their part. If you want to understand how the orchestra sounds, you can either learn how each musician contributes or simply listen to the orchestra as a whole. In the case of structural analysis, the Modal Superposition Principle allows engineers to analyze each mode (musician) to understand and predict the overall response of the structure (orchestra).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modal Superposition Method: A technique to analyze dynamic systems by decoupling into simpler modal equations.
-
Independent Scalar Equations: Each modal equation can be treated separately to simplify complex dynamic analysis.
-
Total System Response: The individual modal responses can be combined to reconstruct the total dynamic response of the system.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing a multi-storey building during an earthquake, each mode of oscillation can be modeled individually to evaluate building responses.
-
In a vibrational analysis of a bridge, various modes are calculated independently before summing their contributions to determine the overall vibrational response.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the world of shifts and shakes, / Separate responses, a choice it makes. / Add them up, with careful looks, / Simple math, no need for books!
📖 Fascinating Stories
-
Imagine a conductor directing an orchestra. Each musician plays their own tune (each mode). After practicing separately, they combine to create a beautiful symphony (the total response). This mirrors the way modal responses come together for the final structural analysis.
🧠 Other Memory Gems
-
Remember 'SIMPLY': Separate, Independent, Modal, summation, for the total, Yield.
🎯 Super Acronyms
M.E.S.S. - Modal Equations Sum to Structure responses!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Superposition Method
Definition:
A technique in structural dynamics that allows the analysis of complex dynamic systems by simplifying the equations of motion into independent modal equations.
-
Term: Modal Equation
Definition:
An individual equation that describes the dynamics of a specific mode of vibration in a system.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate when disturbed from its equilibrium position.
-
Term: Damping Ratio
Definition:
A dimensionless measure describing how oscillations in a system decay after a disturbance.
-
Term: Modal Participation
Definition:
The effective contribution of each mode to the overall response of the system.
-
Term: Modal Truncation
Definition:
The practice of neglecting higher modes in dynamic analysis that have minimal contribution to the overall system response.