Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Design Horizontal Seismic Coefficient
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are discussing the Design Horizontal Seismic Coefficient, or Ah. Ah is essential for calculating how a structure should perform during an earthquake. Can anyone tell me why this is critical for engineers?
It's important because it helps us design buildings that can withstand earthquakes!
Exactly! Now, Ah is determined using a specific formula: Ah = (Z * I * S) / (R * g). What do you think these variables represent?
I think Z is the zone factor indicating seismic risk?
Correct! Each zone has a different Z value, ranging from 0.10 in low-risk areas to 0.36 in the most at-risk zones. Let's move on to the importance factor, I. Can anyone give me an example of its application?
I know that hospitals have a higher importance factor because they need to remain operational after an earthquake.
Great example! Hospitals do have an importance factor of 1.5 for that very reason. Let’s remember that higher usage or occupancy leads to a higher factor. To summarize, Ah helps us predict how our buildings can handle seismic forces, and understanding the components of this formula is crucial.
Components of the Seismic Coefficient
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand what Ah is, let’s dive deeper into its components. First, the Importance Factor I varies based on a structure's purpose. What importance factors do you recall for different structures?
Ordinary buildings have 1.0 for the importance factor while hospitals have 1.5.
Spot on! Now, let’s discuss the Response Reduction Factor, R. It defines how much a building's design is able to reduce the seismic forces through ductility. Can anyone tell me specific R values for common structural systems?
Ordinary moment-resisting frames have R values of 3, while special moment-resisting frames have R values of 5.
Exactly right! The higher the value, the more a frame can let the building absorb seismic forces without failing. Why do you think this is important?
It’s important because it helps protect lives and investments by preventing structural failure.
Well said! Summarizing the key components helps us understand how to design safe buildings in earthquake-prone regions.
Calculation and Application of the Seismic Coefficient
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's apply what we've learned by calculating Ah for a building in Zone IV. If we say the zone factor Z is 0.24, the importance factor I is 1.0, the response reduction factor R is 3, and the spectral acceleration coefficient S/g is 1.5. Who can show me how to plug these values into the formula?
So we would use the formula Ah = (Z * I * S) / (R * g) and substitute the values correctly.
Exactly! If g is approximately 9.81 m/s², what would Ah equal?
Plugging it into the formula, Ah = (0.24 * 1.0 * 1.5) / (3 * 9.81), which gives us an Ah value of approximately 0.0122.
Perfect! Understanding how to calculate Ah helps engineers design structures based on their seismic requirements. Always remember, practice will reinforce this understanding!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Design Horizontal Seismic Coefficient (Ah) is a fundamental parameter in earthquake-resistant design, calculated using the formula Ah = (Z * I * S) / (R * g). This section discusses its components including the zone and importance factors, response reduction factor, and the spectral acceleration coefficient, ensuring engineers can appropriately calculate seismic loads for structures in different seismic zones.
Detailed
Design Horizontal Seismic Coefficient (Ah)
The Design Horizontal Seismic Coefficient (Ah) is crucial for determining the seismic forces acting on a structure. The formula is given as:
$$ A_h = \frac{Z \cdot I \cdot S}{R \cdot g} $$
Key Components:
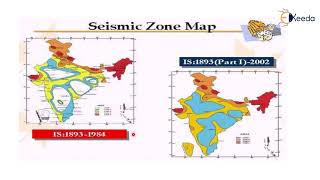
- Z (Zone Factor): This factor, varying from 0.10 to 0.36, indicates the level of seismic risk associated with different regions in India. Higher values represent higher seismic risk zones.
- I (Importance Factor): This factor is dependent on the usage and occupancy of the building. For example, ordinary buildings have an importance factor of 1.0, while hospitals and emergency buildings have a factor of 1.5, recognizing their critical need for stability during seismic events.
- R (Response Reduction Factor): R represents the effectiveness of the structural system in reducing seismic forces through ductility. Typical values are 3 for ordinary moment-resisting frames and 5 for special moment-resisting frames.
- S/g (Spectral Acceleration Coefficient): This coefficient reflects the anticipated acceleration experienced by a structure during seismic activity.
Understanding and accurately applying the design horizontal seismic coefficient is essential for ensuring the safety and resilience of structures in earthquake-prone areas.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Formula for Design Horizontal Seismic Coefficient (Ah)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Z I S
A = · · a
h 2 R g
Detailed Explanation
The formula for calculating the Design Horizontal Seismic Coefficient (Ah) involves several factors. Each component of the formula plays a crucial role:
- Z (Zone factor): This represents the seismic zone where the building is located, reflecting the expected ground shaking.
- I (Importance factor): This accounts for the significance of the building's use; for instance, hospitals have a higher importance factor due to their role in emergencies.
- S /g (Spectral acceleration coefficient): It indicates how the structure will respond to different frequencies of ground motion.
- R (Response reduction factor): This relates to the capacity of the building's design to withstand seismic forces without collapsing.
- g: This is the acceleration due to gravity.
Combining these elements allows engineers to determine how much horizontal force the structure must resist during an earthquake.
Examples & Analogies
Think of the formula like a recipe for a cake. Each ingredient (Z, I, S, R) must be measured correctly to create the perfect balance for stability. If you omit or miscalculate any ingredient, just like with baking, your final result will not hold up to the stress it’s meant to withstand.
Importance Factor (I)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Depends on the use and occupancy.
• E.g., 1.0 for ordinary buildings, 1.5 for hospitals, emergency buildings.
Detailed Explanation
The Importance Factor (I) varies based on how the building will be used. It’s a multiplier that adjusts the earthquake resistance needed for structures based on their role:
- Ordinary Buildings: For normal usage, such as residences or offices, the importance factor is set to 1.0, meaning standard design practices apply.
- Hospitals and Emergency Buildings: These structures are deemed critical during emergencies and thus have an increased importance factor of 1.5, indicating they need to be more robust to withstand earthquake forces without risking lives.
Examples & Analogies
Imagine a standard home as a basic shield against rain — it needs to withstand daily weather. However, a hospital is like a storm shelter; it must be reinforced to ensure safety, even in the most extreme conditions. Therefore, its design is more rigorous.
Response Reduction Factor (R)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Depends on the structural system and ductility.
• E.g., 3 for ordinary moment resisting frame (OMRF), 5 for special moment resisting frame (SMRF).
Detailed Explanation
The Response Reduction Factor (R) is another crucial aspect that indicates how much a structural system can reduce seismic forces due to its inherent flexibility and energy-dissipating capabilities. Different structures will have different response reduction factors depending on their design:
- Ordinary Moment Resisting Frame (OMRF): For structures that are not specifically designed to endure heavy seismic activity, the factor is 3, indicating limited ability to absorb shock.
- Special Moment Resisting Frame (SMRF): These buildings have enhanced design features that allow them to better absorb and dissipate seismic energy, hence a higher factor of 5 reflects a greater capacity to resist earthquakes.
Examples & Analogies
Consider two athletes: one can run 100 meters at a steady pace (OMRF) and the other can sprint with bursts of speed and take sharp turns (SMRF). The second athlete (SMRF) is better at maneuvering under pressure, akin to a building that can flexibly adapt to seismic forces.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Design Horizontal Seismic Coefficient (Ah): Essential for determining seismic loads based on several factors.
-
Zone Factor (Z): Indicates the seismic risk of a region, varying from low to high.
-
Importance Factor (I): Reflects how critical the building's use is regarding safety and functionality during seismic events.
-
Response Reduction Factor (R): Represents the structural system's ability to reduce ground motion effects through flexibility and ductility.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a hospital located in a Zone V area, the calculated Ah value would be higher due to its importance factor of 1.5, ensuring it can withstand greater seismic forces.
-
An ordinary residential building in Zone III, with a lower zone factor and importance factor, will have a significantly lower Ah value.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Ah for structures, we design, keep them safe when the earth does align.
🧠 Other Memory Gems
-
Remember 'ZIRS': Zone, Importance, Response, Spectral for Ah calculation simplicity.
📖 Fascinating Stories
-
Imagine a hospital standing tall in an earthquake, its design's faith resting on the Importance Factor, protecting lives with resilience.
🎯 Super Acronyms
Use 'ZIRS'—Zone, Importance, Response, and Spectral to recall the key factors for calculating Ah.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Design Horizontal Seismic Coefficient (Ah)
Definition:
A coefficient used to calculate the seismic loads on structures based on various factors including seismic zone and building importance.
-
Term: Zone Factor (Z)
Definition:
A numerical value representing the seismic risk level of a specific geographical area.
-
Term: Importance Factor (I)
Definition:
A multiplicative factor reflecting the significance of a building's usage in relation to its seismic performance.
-
Term: Response Reduction Factor (R)
Definition:
A factor that accounts for the reduction in seismic forces due to the ductility of the structural system.
-
Term: Spectral Acceleration Coefficient (S/g)
Definition:
A coefficient that relates to the expected ground shaking intensity at a site.