Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Base Shear
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to talk about base shear, which is the total lateral force acting at the base of a building during an earthquake. Why do you think it is important to calculate?
I think it helps us know how much force a building needs to withstand.
And maybe how to design the structure so it doesn't collapse?
Exactly! Base shear is crucial for ensuring that the design can sustain seismic loads. The distribution of this shear along the height of the building is particularly vital for managing forces.
How is that distribution calculated?
Great question! We use the formula involving the seismic weight and height of each level of the building. Let's dive into that!
Formula for Lateral Force
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The formula used for calculating the lateral force at level i is `Fᵢ = (Wᵢ · hᵢ² / Σ(W · h²)) · V`. Can anyone break down what each variable represents?
Fᵢ is the force at the i-th level, right?
Correct! And what about Wᵢ?
That would be the seismic weight at level i.
Exactly! And hᵢ is the height from the base to that level. Why do you think we square the height in the formula?
Maybe because the effects of force increase with height?
Yes! The forces become more significant as the height increases. Let's summarize this section.
Significance of Distribution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Why do you think understanding the distribution of base shear is important?
It helps us locate where to strengthen parts of the building.
Yes, different floors might need different supports!
Absolutely! In fact, buildings with more floors often experience different magnitudes of force at various heights due to this distribution. Being aware of this helps engineers develop appropriate structural solutions.
So, it’s not just about the bottom floor?
Exactly! All levels must work together to resist seismic forces. Let's quickly summarize what we've learned today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the formula used to determine the lateral force experienced at different floor levels during seismic events. The distribution of base shear is critical for understanding how a structure will react under seismic loads, ensuring effective design and safe construction.
Detailed
Distribution of Base Shear along Height
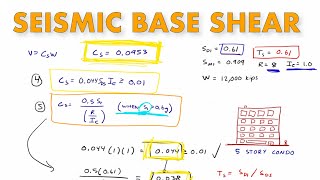
In earthquake engineering, the distribution of the base shear along the height of a building is essential for designing earthquake-resistant structures. The lateral force at any floor level (represented as Fᵢ) can be calculated using the formula:
Fᵢ = (Wᵢ · hᵢ² / Σ(W · h²)) · V
Where:
- Fᵢ: Lateral force at level i.
- Wᵢ: Seismic weight at level i.
- hᵢ: Height of level i from the base.
- V: Total base shear.
This formula essentially states that the lateral force acting on each floor is proportional to its seismic weight and the square of its height above the base, normalized by the total seismic weight times the height squared of all levels. This approach ensures that taller structures experience greater lateral forces at upper levels, which is crucial for maintaining stability and integrity during seismic events.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Lateral Force at Floor Level
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The lateral force at any floor level is given by:
\[ F_i = \frac{W_i \cdot h_i^2}{\sum W_j \cdot h_j^2} \cdot V \]
Where:
- F_i : Lateral force at level i
- W_i : Seismic weight at level i
- h_i : Height of level i from base
Detailed Explanation
This formula expresses how the lateral force (the force acting horizontally due to seismic activity) is distributed across different floors of a building. \(F_i\) represents the lateral force at a specific floor (level i). The seismic weight (\(W_i\)) of that floor and its height (\(h_i\)) from the base contribute to the calculation. The sum in the denominator accounts for all the floors below it, ensuring that the force distribution reflects the building's entire height and weight. The total base shear, \(V\), is applied to determine the forces acting on each individual floor based on these heights and weights.
Examples & Analogies
Imagine you're on a multi-story parking garage during a shake. The floors at the top might sway more than the ground floor. This is similar to how the forces distribute; lighter (or less stable) sections of a building might experience greater shaking, just like lighter cars at the top of a tall garage moving more than those on the ground.
Understanding Seismic Weight
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
- W_i : Seismic weight at level i
- h_i : Height of level i from base
- j : Index running over all floors in the building
Detailed Explanation
In the equation, \(W_i\) is the seismic weight specific to each floor, which includes the weight of structural elements and a portion of the live load (like furniture or occupants). The height, \(h_i\), measures how far that floor is from the base, which influences its contribution to the overall force experienced during an earthquake. Essentially, higher floors have a greater effect on the distribution of seismic force due to their height.
Examples & Analogies
Think of how a swing moves. The higher you pull the swing, the more it will sway. Similarly, in buildings, the height of the floor affects how much force it feels during an earthquake. The floors higher up experience more movement, just like a swing at its peak.
Sum of Weight Heights
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
- j : Index running over all floors in the building
Detailed Explanation
The sum in the denominator totals the seismic contributions of all the floors in the building. Each floor has a certain weight and height combination, and adding these together helps calibrate how strong the forces are at different levels. This ensures that the most accurate calculations for the lateral forces at each floor are derived, reflecting the overall structure's response during seismic activities.
Examples & Analogies
Imagine a packing scale, where each item (floor) has a different weight. When you put everything on, the scale shows the total weight. In our case, the 'scale' balances the effects of all the different floors to find out how forces change across the structure when an earthquake occurs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Base Shear: Total lateral force at the base due to seismic activity.
-
Lateral Force: The force distributed at each level based on seismic weight and height.
-
Seismic Weight: The total weight that contributes to the seismic forces acting on a building.
-
Height Dependency: Higher levels of a building experience more seismic forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider a multi-story building where the total weight at the top is much lighter than that at the bottom. In such cases, the upper floors will experience lateral forces proportional to their weight and height relative to the base.
-
Imagine a 10-story building where the first floor experiences a lateral force of 50 kN while the top floor might experience a force of 20 kN, due to varying weights and heights.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Base shear is what we must hear, at the base is where it sways, to keep our structures safe always.
📖 Fascinating Stories
-
Once, there was a tall tower that trembled during an earthquake. The heavier lower floors held the upper floors steady, ensuring the tower didn’t topple. This story reminds us of why weight distribution matters.
🧠 Other Memory Gems
-
W-H-F: Weight must factor in Height for effective Force distribution.
🎯 Super Acronyms
B-S-H
- Base Shear’s Height affects stability in seismic conditions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Base Shear (V)
Definition:
The total lateral force acting on a structure at its base during an earthquake.
-
Term: Lateral Force (Fᵢ)
Definition:
The force experienced at a specific level of the building due to seismic activity.
-
Term: Seismic Weight (Wᵢ)
Definition:
The effective weight for seismic design at each level of a building, based on dead and live loads.
-
Term: Height (hᵢ)
Definition:
The vertical distance of a specific floor level from the base of the structure.