Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equation
Unlock Audio Lesson
Today, we'll start learning about Bernoulli's Equation. Can anyone tell me what we generally understand by fluid flow and energy?
Fluid flow involves the movement of liquids or gases, and energy accounts for pressure and velocity, right?
Exactly! We can look at fluid motion through the concept of 'virtual fluid balls.' It helps us visualize the kinetic and potential energies in the flow. Stress the importance of visualizing flow through streamlines.
So these streamlines help us understand how pressure changes along a flow?
Yes! Remember, the pressure, velocity, and height together form the basis of Bernoulli's Equation. We represent this through our virtual fluid balls!
Are there any specific conditions we must meet to properly apply this equation?
Great question! We must ensure the flow is frictionless, incompressible, and steady. We’ll explore these assumptions and their implications.
So we can't use Bernoulli's Equation close to solid surfaces?
Correct! Close to solids, friction comes into play, which the equation doesn't account for. Always analyze the flow conditions before applying the equation.
To recap, Bernoulli's Equation connects pressure, kinetic energy, and potential energy in fluid flowing along streamlines. Remember its limitations while applying, such as friction and flow type.
Limitations and Misuse of Bernoulli's Equation
Unlock Audio Lesson
Now, let’s discuss limitations in applying Bernoulli's Equation. What do you think might be a reason we can't apply it everywhere?
I assume because sometimes the flow isn't steady or there's significant friction?
Absolutely! Additionally, it doesn't apply to compressible flows if density changes are critical. Can anyone explain the significance of the Mach number here?
Uh, it identifies how compressible the flow is. Below Mach 0.3, flows tend to be treated as incompressible.
Right! Good job! Let’s not forget that Bernoulli's can be misused, especially in areas where energy losses occur.
Where are those losses predominantly found?
Let's take turbulence and viscous flow near solids. Remember these zones and identify them in problems.
To summarize today, Bernoulli's Equation is powerful, but it has its limitations. Always check the flow state, potential friction, and possible energy losses.
Application of Bernoulli's Equation
Unlock Audio Lesson
Let’s earn how we apply Bernoulli's Equation practically, starting with the relationship between velocity at a nozzle and tank water level. Who can outline these concepts?
Based on the height, the velocity of the fluid will be influenced by the pressure from the height.
Yes, right! Imagine there are 'virtual balls' representing the flow. Can someone explain how we'd set up Bernoulli's between two points in this scenario?
At the water's surface, we'd reference the atmospheric pressure, then compare it to the nozzle exit pressure.
Excellent! You’ll find that velocity from height would be akin to free fall. Is there a formula you all can derive from Bernoulli's that relates height to velocity?
Yes! We can derive that V equals the square root of 2gh, considering pressure at the day is atmospheric.
Great work! Also, acknowledge that as practical flows have real energy losses, we also adjust with a discharge coefficient.
So the coefficient adjusts for real-world effects from friction and flow variances?
Exactly! To conclude, we can apply Bernoulli's with care, always factoring in real-world conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Applying Bernoulli's Equation involves understanding fluid dynamics concepts, particularly how potential and kinetic energies relate to fluid flow. The section emphasizes the importance of visualizing streamlines, understanding pressure variations, and recognizes the equation's limitations when applied to real-world scenarios.
Detailed
Applying Bernoulli's Equation
In this section, we explore the application of Bernoulli's Equation, a fundamental tool in fluid dynamics. The key takeaway is that Bernoulli's Equation connects pressure, velocity, and height in a fluid system, allowing us to determine how these variables interact along a streamline. The visualization of fluid as 'virtual balls' helps in conceptualizing flow energy.
Key Concepts
- Flow Energy per Weight: Each fluid element contributes to the overall energy, quantified through pressure and area changes.
- Streamlines: Essential for correctly applying Bernoulli's Equation; understanding pressure and kinetic energy at different points along the streamline is crucial.
Limitations of Bernoulli's Equation
While powerful, Bernoulli's Equation has limitations:
- Frictionless Flow: It assumes no friction or shear stress, making it only applicable to idealized cases.
- Unsteady Flow: The simplified form is mainly for steady flow; complexities arise when time components come into play.
- Incompressible Flow: It is applicable when the flow conditions (Mach number < 0.3) involve negligible density changes.
In conclusion, to effectively use Bernoulli's Equation, one must recognize these limitations and visually represent the flow to avoid misapplication.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Motion with Virtual Balls
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a virtual fluid ball is moving from one location to two locations, since it is a virtual fluid ball, we consider there are n number of fluid balls. They have a pressure exerting on one another. This leads to flow energy, which we quantify as pressure times area times delta x.
Detailed Explanation
The first concept we introduce is the idea of visualizing fluid motion using virtual balls. Imagine a fluid made up of many small balls that can move through a space. When these balls are in motion, they influence each other through pressure forces, creating a flow of energy. We quantify this flow energy using a simple formula: Pressure multiplied by Area multiplied by the distance (delta x) they travel. This helps us to understand how fluids behave when they flow in different conditions.
Examples & Analogies
Think of a balloon filled with air. When you squeeze one side of the balloon, the air inside pushes against the walls, causing the air to move toward the opposite side. In this example, the air acts like the virtual balls, moving and exerting pressure on each other to create flow.
Applying Bernoulli's Equation Along Streamlines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
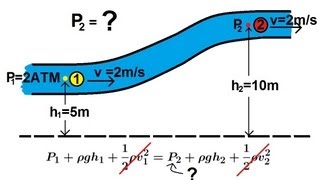
Whenever you apply the Bernoulli equation, you should draw the streamlines to visualize how the fluid moves. Knowing the pressure variability and the velocity at two points allows you to solve problems.
Detailed Explanation
When you want to apply Bernoulli's equation, it's crucial to visualize the flow of fluid along streamlines. This means drawing lines that represent the path a fluid particle takes as it moves. By identifying the pressures and velocities at various points along these lines, you can effectively use Bernoulli's equation to derive relationships between different factors in fluid motion. This understanding is essential for solving real-world fluid dynamics problems where velocities and pressures change.
Examples & Analogies
Imagine a river with different currents. If you wanted to measure how fast the water flows at different points, you'd need to observe and mark the streamlines of the water. By measuring the height of the river and the speed of the current at two points, you could apply Bernoulli's principle to find out how fast the water will flow or how high it can rise.
Limitations of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Bernoulli's equation has limitations: it applies best in steady flow, is frequently misused, and requires assumptions like incompressible flow and frictionless conditions. Additionally, it cannot be applied near solid surfaces due to shear stress and viscous effects.
Detailed Explanation
Bernoulli's equation is a powerful tool in fluid dynamics, but it has its limits. It works well under steady flow conditions and when the flow can be approximated as incompressible and frictionless. However, in real situations, especially near solid surfaces where the fluid experiences resistance, the assumptions behind Bernoulli's equation may not hold. This often leads to misuse and inaccurate results in fluid behavior analysis if these conditions are not properly considered.
Examples & Analogies
Consider a water slide at a theme park. While Bernoulli's equation predicts smooth flow down the slide, if someone stands at the bottom, the friction between the water and the slide increases, altering the flow. Thus, while Bernoulli's principle helps explain how water moves, it doesn't account for the additional challenges posed by friction or changes in velocity and pressure near solid objects.
Application of Bernoulli's Principle with Wind Tunnels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When conducting tests in a wind tunnel, you must recognize where Bernoulli's equation can validly be applied. Frictional effects near walls make it important to determine where the flow remains valid.
Detailed Explanation
In wind tunnel testing, Bernoulli's equation can provide valuable insights into how air flows over a model. However, the proximity of the model to the walls creates frictional effects that can distort the flow. It's essential to understand these limitations to ensure that the Bernoulli equation is applied correctly in analyzing fluid dynamics. This typically involves ensuring that the measurements are taken where the air flows freely without significant interference from surface friction.
Examples & Analogies
Think of a car passing through a narrow alley. The closer the car gets to the walls, the more wind resistance it faces, which can alter its speed and movement. Similarly, in a wind tunnel, as the air moves close to walls, it experiences resistance, which must be accounted for when interpreting the results of the experiments.
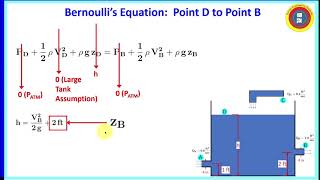
Calculating Velocity and Height Relationship Using Bernoulli's Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
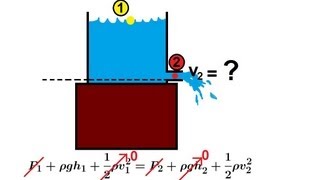
By applying Bernoulli's equation between two points in a tank, we can find a relationship between the nozzle discharge velocity and the height of the water in the tank.
Detailed Explanation
In fluid mechanics, a common application of Bernoulli's equation is to find how the velocity of fluid exiting a nozzle is related to the height of fluid in a tank. By considering one point at the water's surface (where the velocity can be assumed to be zero) and one point at the nozzle's exit, you can apply Bernoulli's principle to establish a mathematical relationship. This involves balancing potential energy, flow energy, and kinetic energy to derive the relationship necessary for practical calculations.
Examples & Analogies
Imagine standing by a garden hose with water flowing out of it. When you turn on the faucet, the water height builds up in the hose, increasing the force with which it shoots out the nozzle. This height can be used to estimate how fast the water comes flowing out. The higher the water in your tank, the faster it will exit, just as your nozzle's speed changes with the water level.
Including Real-World Adjustments with Coefficients of Discharge
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the real world, velocity calculations must account for factors like friction and non-uniform flow, captured by a discharge coefficient (cd) ranging from 0.6 to 1.0.
Detailed Explanation
In practical applications, fluid behavior often deviates from ideal conditions due to factors such as friction and turbulence. To account for these real-world effects, engineers introduce a discharge coefficient (cd), which modifies theoretical calculations to reflect practical observations. This coefficient typically varies between 0.6 (for highly turbulent flows) to 1.0 (ideal situations). By applying the cd correction when calculating discharge through nozzles, engineers can effectively predict flow rates more accurately.
Examples & Analogies
Think of a straw. If you're drinking a thick smoothie, it’s harder to suck up than plain water; the viscosity creates more friction. The discharge coefficient for your drinking experience would be lower for the smoothie than for water. Similarly, engineers use a discharge coefficient to adjust calculations in real-life fluid scenarios to reflect similar structural inefficiencies.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Flow Energy per Weight: Each fluid element contributes to the overall energy, quantified through pressure and area changes.
-
Streamlines: Essential for correctly applying Bernoulli's Equation; understanding pressure and kinetic energy at different points along the streamline is crucial.
-
Limitations of Bernoulli's Equation
-
While powerful, Bernoulli's Equation has limitations:
-
Frictionless Flow: It assumes no friction or shear stress, making it only applicable to idealized cases.
-
Unsteady Flow: The simplified form is mainly for steady flow; complexities arise when time components come into play.
-
Incompressible Flow: It is applicable when the flow conditions (Mach number < 0.3) involve negligible density changes.
-
In conclusion, to effectively use Bernoulli's Equation, one must recognize these limitations and visually represent the flow to avoid misapplication.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When water flows from a tank through a nozzle, its velocity increases according to the height difference due to Bernoulli's Equation.
-
In a wind tunnel experiment, Bernoulli's Equation cannot apply when viscous effects dominate near walls.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluid flows with graceful ease, Bernoulli’s laws explain the tease.
📖 Fascinating Stories
-
Imagine a fluid ball rolling down a hill, gaining speed as it descends; just like it, Bernoulli’s Equation describes the flow's thrill.
🧠 Other Memory Gems
-
P.V.H. - Pressure, Velocity, Height: The trio of Bernoulli's insight!
🎯 Super Acronyms
B.E. - Bernoulli's Equation
- Connecting energy in motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli's Equation
Definition:
A principle in fluid dynamics that describes the relationship between pressure, velocity, and height in a flowing fluid.
-
Term: Streamline
Definition:
A line that represents the flow of fluid, indicating the velocity of flow at various points.
-
Term: Incompressible Flow
Definition:
Flow where the fluid density remains constant, typically applicable at Mach numbers less than 0.3.
-
Term: Discharge Coefficient
Definition:
A correction factor used to account for losses in flow due to friction and turbulence.
-
Term: Virtual Fluid Balls
Definition:
A conceptual model for visualizing the movement of fluid elements through streamlines in fluid dynamics.