Practical Applications of Bernoulli's Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Visualization of Fluid Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Alright class, let’s begin by discussing how we can visualize fluid flow. Imagine a series of balls moving along a path; this helps us understand the streamlines.

So, are those balls like tiny bits of fluid in motion?

Exactly! These 'virtual fluid balls' represent how fluid elements move. Drawing these lines allows us to apply Bernoulli's Equation between any two points on a streamline.

Does that mean we can only use Bernoulli's Equation along these lines?

Correct! Always ensure you're applying it along a streamline where flow conditions are consistent.

What happens if the streamlines aren't straight?

Good question! Non-straight streamlines indicate complex flow, potentially invalidating Bernoulli’s assumptions. Visualizations remain crucial!

Could you summarize why visualization is key?

Certainly! Visualizing flow allows us to identify applicable scenarios for Bernoulli's Equation and understand energy conservation in fluids.
Conditions for Applying Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s dive into the conditions necessary for applying Bernoulli’s Equation. What do you remember?

The flow should be steady and frictionless, right?

Right! It should also be incompressible. Why do you think that’s important?

Because if there are density changes, the energy calculations could be wrong?

Exactly! A flow must maintain consistent density for Bernoulli's principles to hold true. Any variations affect energy conservation.

Can you give us an example of a situation where it wouldn't apply?

Sure! In situations with high flow velocities, like near solid surfaces where viscosity influences behavior, Bernoulli's Equation becomes inaccurate.

Can we use it for all types of flows?

Not all! It’s typically best for flows with a Mach number less than 0.3 to approximate incompressibility.
Limitations of Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore the limitations of Bernoulli’s Equation. Why do you think recognizing these limitations is essential?

To avoid errors in engineering problems?

Exactly! For instance, we can’t apply it near surfaces due to friction. What are some other restrictions we need to be aware of?

Mixing zones can also cause issues!

Exactly! Mixing zones disrupt energy conservation assumptions. Always assess flow conditions before applying the equation.

So, we have to be careful about analyzing high-energy systems, right?

Precisely! Situations involving pumps or turbines introduce additional complexities that demand thorough analysis.
Applications of Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, who can give me some practical applications of Bernoulli’s Equation in engineering?

I think it’s used to calculate flow rates from nozzles!

Excellent! Can you elaborate on how that works?

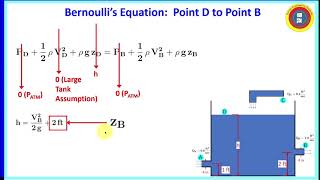
We can apply it from the tank surface to the nozzle to find velocities.

What about pressure distributions in pipes?

Exactly! In pipe systems, Bernoulli's can help analyze how pressure changes along the pipe length.

Can it also work for different height situations?

Yes! By understanding height differences, you can determine changes in velocity and pressure at different points.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Bernoulli's Equation serves as a fundamental principle in fluid mechanics, applicable primarily under conditions of steady, incompressible, and frictionless flow. The section outlines the necessity of drawing streamlines to visualize fluid movement and emphasizes the limitations of the equation, particularly regarding friction and unsteady flows.
Detailed
Practical Applications of Bernoulli's Equation
Bernoulli's Equation is a vital tool in fluid mechanics used to describe the behavior of flowing fluids under specific conditions. The equation emphasizes the conservation of energy in fluid flow, integrating kinetic energy, potential energy, and flow energy. Essential points discussed in this section include:
- Visualization of Flow: It is crucial to visualize fluid flow by drawing streamlines, which represent the paths followed by fluid elements. This aids in understanding the application of Bernoulli's Equation between two points along the stream.
- Conditions for Application: Bernoulli's Equation is most valid under steady flow conditions (no time component), incompressible flow (density variations are negligible), and for frictionless scenarios, making it suitable for many engineering applications where the Mach number is less than 0.3.
- Limitations: The section discusses significant limitations including:
- It cannot be applied in regions with significant friction or near solid surfaces where viscous effects dominate.
- Mixing zones and scenarios involving shaft work (e.g., pumps and turbines) must be carefully treated.
- Applications in Engineering: When applied correctly, Bernoulli's Equation simplifies the analysis of various engineering problems, such as calculating flow velocities from nozzles and understanding pressure distributions in pipes.
By recognizing the conditions under which Bernoulli's Equation is applied, engineers can effectively utilize the equation to solve practical fluid flow problems.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Visualizing Fluid Motion with Virtual Fluid Balls
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, if you think about it, instead of understanding or deriving along the streamlines, we can visualize it as a virtual fluid balls moving from one location to another. We consider there are n number of fluid balls, each having pressure interacting with one another, generating flow energy, which we quantify into pressure multiplied by area multiplied by delta x.
Detailed Explanation
This chunk explains how we visualize fluid motion using the concept of virtual fluid balls. By imagining these balls, we can better understand the interactions of fluid particles as they move along streamlines. Each fluid ball represents a small portion of fluid that experiences pressure forces, and the collective behavior of these balls helps us quantify the flow energy. In essence, these virtual fluid balls simplify the complexities involved in fluid dynamics, making it easier to apply Bernoulli's Equation.
Examples & Analogies
Think of it like a group of dancers moving in sync across a stage (the fluid balls). Each dancer interacts with those around them, and together they create a flow of movement (the fluid flow). Just as you can visualize the rhythms and paths of the dancers, we use virtual balls to visualize how fluid moves and interacts.
Key Assumptions of Bernoulli's Equation
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The most important assumption is that the flow is frictionless. This means it cannot be applied near a solid surface, as viscosity and shear stress become significant. Other factors like mixing zones and shaft work from machinery also restrict the application of Bernoulli's Equation.
Detailed Explanation
Here, we explore key assumptions that must hold true for Bernoulli's Equation to be applicable. Frictionless flow assumes that there are no energy losses due to drag from pipe walls or boundaries. When a fluid flows near a solid surface, like a pipe, viscous effects create friction, which means we cannot use Bernoulli's Equation effectively in such scenarios. Additionally, in systems where external forces (like pumps) affect the flow, we need to be mindful of these influences as they complicate the behavior of fluid.
Examples & Analogies
Imagine a smooth sled sliding down an ice ramp (frictionless flow) versus a sled on a dirt hill (frictional flow). On the ice, the sled moves easily without resistance, similar to how fluids move in ideal conditions dictated by Bernoulli's Equation. On dirt, however, the friction slows it down and complicates the sled's path, much like how real-world conditions impede fluid flow.
Applying Bernoulli's Equation: Steps for Success
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Whenever you apply the Bernoulli equation, you should draw the streamlines and visualize how the fluid moves. Understand the pressure variability between points and solve problems based on the known pressure and velocity.
Detailed Explanation
This chunk emphasizes the process of applying Bernoulli's Equation correctly. Before attempting to solve problems, it is crucial to sketch the streamlines that represent the path of the fluid. This visualization aids in understanding how pressure and velocity change from one point to another. By knowing either pressure or velocity, we can tackle most fluid problems systematically using Bernoulli's Equation.
Examples & Analogies
Think of using a map to navigate a new city. You wouldn't just drive without knowing your route; you need to see where you're going to understand the right turns and speeds. Similarly, drawing streamlines before applying Bernoulli's Equation helps us navigate through fluid dynamics and solve for unknown variables.
Understanding Limitations of Bernoulli's Equation
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Bernoulli's Equation is frequently misused because it can only be applied to steady, incompressible flow. For cases where the flow is unsteady or compressible, it is essential to recognize these limitations.
Detailed Explanation
In this chunk, we discuss the common pitfalls of using Bernoulli's Equation. Its effectiveness is limited to scenarios characterized by steady and incompressible flow. If the flow changes with time (unsteady) or if there are significant changes in density (compressible), the equation does not apply accurately. Recognizing these limitations is crucial to avoid erroneous conclusions in fluid mechanics.
Examples & Analogies
It's like following a recipe for baking bread. If you stray too far from the instructions (like using the wrong ingredients or mixing techniques), the end result won't be what it should be. Similarly, if we apply Bernoulli's Equation outside its valid conditions, the results will not accurately represent the flow phenomenon.
Practical Applications in Engineering
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In civil and mechanical engineering, many fluid flow problems can be treated as incompressible when the flow is at low speeds (Mach number less than 0.3). This consideration simplifies many practical applications.
Detailed Explanation
This chunk highlights the practical implications of applying Bernoulli's Equation in engineering fields. For most fluid flows encountered at low speeds, engineers can assume the fluid is incompressible, which simplifies problem-solving. This assumption holds valid because density variation is often minimal, allowing for straightforward applications of Bernoulli's Equation in predicting behavior in pipes, channels, and other fluid systems.
Examples & Analogies
Consider a water supply system in a city. Engineers assess fluid flow under conditions where the flow speeds are relatively low. By treating water as incompressible, they can easily calculate pressures and velocities needed for effective design, much like how a gardener can accurately predict how much water to use based on a simple formula, given that the water's density doesn't significantly change.
Key Concepts
-
Application of Streamlines: Important for visualizing fluid movement to apply Bernoulli's Equation effectively.
-
Conditions for Validity: Bernoulli's Equation is valid for steady, incompressible, and frictionless flows.
-
Limitations of the Equation: Cannot be applied in high-friction environments or mixing zones.
-
Practical Uses: Valuable in engineering for computations related to flow rates and pressure distributions.
Examples & Applications
Calculating the exit velocity of a fluid from a nozzle using Bernoulli's Equation.
Analyzing the pressure distribution in a pipe system to determine flow conditions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Steady, smooth, and low resist, Bernoulli's flow is hard to miss!
Stories
Once upon a time, fluid balls raced down a river. They flowed smoothly over rocks and hills, feeling light as air. But near the rocky banks, they slowed down, realizing friction made them lose their speed.
Memory Tools
Remember 'SIF' for Bernoulli: Steady, Incompressible, Frictionless.
Acronyms
Use 'FKE' for Fluid Kinetic Energy
Flow energy = Kinetic energy + Potential energy.
Flash Cards
Glossary
- Bernoulli’s Equation
A principle in fluid dynamics that describes the conservation of energy in flowing fluids.
- Streamline
A curve that is tangent to the velocity of the flow, representing the path of fluid elements.
- Incompressible Flow
Fluid flow in which the density of the fluid remains constant.
- Pressure Gradient
The rate at which pressure changes in a fluid per unit distance.
- Flow Energy
The energy associated with the movement of fluid, calculated as pressure times area times distance.
Reference links
Supplementary resources to enhance your learning experience.
